吴恩达机器学习课程逻辑回归正则化python实现【对应ex2-ex2data2.txt数据集】
写在前面
1.本篇笔记是对ex2data2.txt数据集逻辑回归的正则化处理，文中代码是基于上篇笔记的代码的基础上修改。
2.文中没有叙述完整的流程，只叙述了实现正则化需要对上篇笔记中的代码修改的地方。
1. 过拟合
在线性模型和线性分类器中，特征个数过多时容易出现过拟合问题，此时代价函数非常趋近于0或直接等于0。解决过拟合有两种方式，一是通过减少特征的方式，另外一种是保留所有的特征，使用正则化的方式。
2.正则化的目的
训练机器学习模型的要点之一是避免过拟合。如果发生过拟合，模型的精确度会下降。这是由于模型过度尝试捕获训练数据集的噪声导致的。正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。对于线性模型，譬如线性回归、逻辑回归，可以使用简单有效的参数范数模型进行正则化。许多正则化方法通过对目标函数J添加惩罚项。
3.正则化的分类
正则化后的损失函数如下：
根据惩罚项的不同正则化分为L1正则化和L2正则化。
我们使用L2正则项对代价函数进行正则化。
4.逻辑回归代价函数正则化
逻辑回归正则化后的代价函数如下：
代价函数对应的向量化形式为：
J ( θ ) = 1 m [ − y T l o g ( h ) − ( 1 − y ) T l o g ( 1 − h ) ] + λ 2 m θ T θ J(θ) = \frac{1}{m}[-y^Tlog(h)-(1-y)^Tlog(1-h)]+\frac{λ}{2m}θ^Tθ J(θ)=m1[−yTlog(h)−(1−y)Tlog(1−h)]+2mλθTθ
对应的python代码为：
# 定义代价函数
def cost(theta, X, y, lam):
return np.mean(-y * np.log(sigmoid(theta, X)) - (1 - y) * np.log(1 - sigmoid(theta, X))) + lam / (
2 * len(theta)) * (
theta.T @ theta)
求导后的代价函数为：
θ j = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] θ_j = θ_j-α[\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{λ}{m}θ_j] θj=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
5.梯度函数正则化
观察4中求导后的代价函数可得，梯度在未正则化的基础上添加了
，因此正则化后对应的梯度函数也需要修改。对应的python代码如下：
# 梯度函数
def gradient(theta, X, y, lam):
return (1 / len(X)) * (X.T @ (sigmoid(theta, X) - y) + lam * theta)
6.主函数
'''主函数'''
if __name__ == '__main__':
# 数据观察
# x1, y1, x2, y2 = import_data()
# draw(x1, y1, x2, y2)
# 预测函数的阶数
degree = 6
data, label = init_data("data/ex2data2.txt", degree)
# 初始化theta, 特征个数 = (阶数+1)*（阶数+2）/2
feature_number = int((degree + 1) * (degree + 2) / 2)
theta = np.zeros((feature_number, 1))
#正则化参数lambda
lam = 2
# 使用minimize函数求解
result = opt.minimize(fun=cost, x0=theta, args=(data, label, lam), method='Newton-CG', jac=gradient)
# 数据校验
check(result.x, "data/ex2data2.txt", degree)
# 绘制预测图像
decision_boundary(np.mat(result.x).transpose(), degree)
7.运行结果
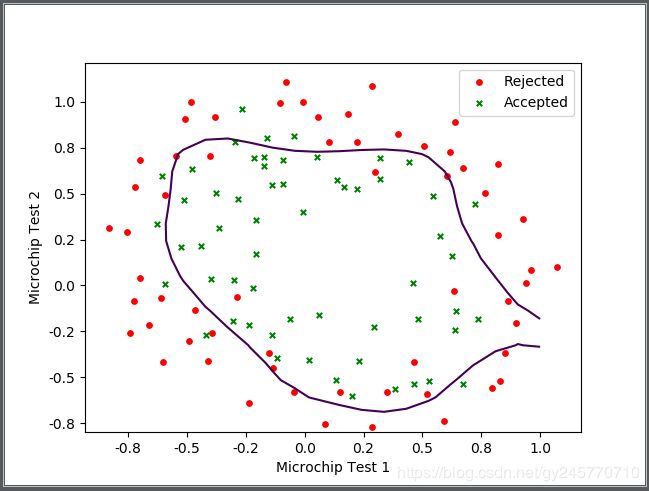
[1] 未正则化的边界函数图像：
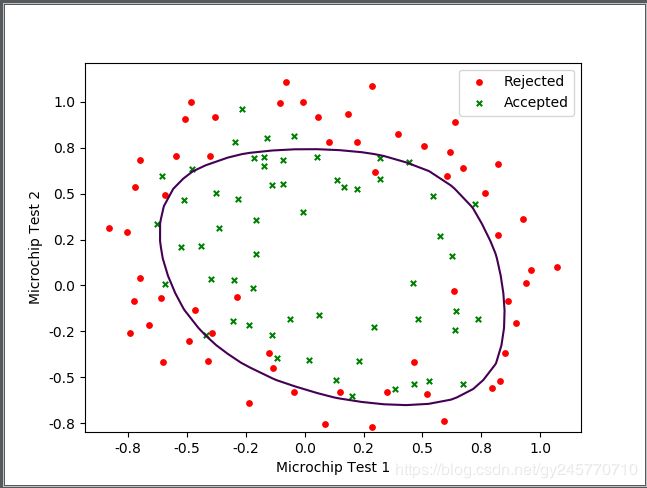
[2]lambda参数为0.1时边界函数图像：
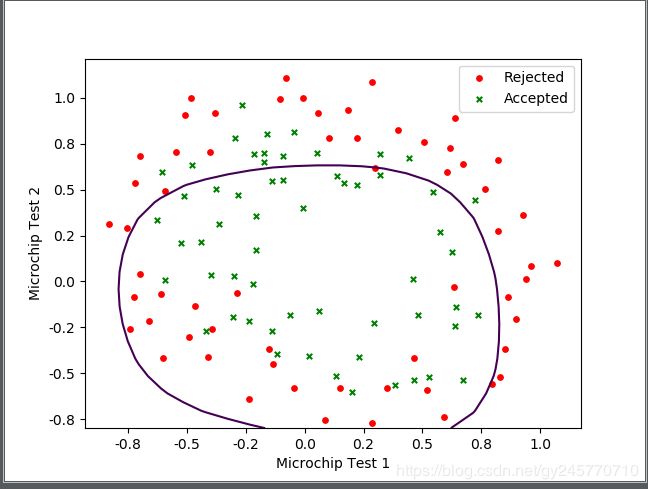
[3]lambda参数为2时边界函数图像：
观察3幅图像可看出，第1幅图像曲线比较弯曲，与训练集数据非常拟合。第2幅图像的曲线非常平滑，并且预测效果比较准确。第3幅图像曲线虽然非常平滑，但是预测效果非常差，属于欠拟合。因此，当lambda=0.1时比较好的解决了过拟合的问题。
8.参考文献
[1] https://www.jiqizhixin.com/articles/2017-11-23-4