STL中的map和unordered_map选择

基本概念

map

map在底层使用了红黑树来实现，在头文件map中我们可以找到这样一句话

ordered red-black tree of {key, mapped} values, unique keys

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，红黑树则还要满足以下五个性质:

性质1 节点是红色或黑色。

性质2 根节点是黑色。

性质3 每个叶节点（NIL节点，空节点）是黑色的。

性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。一个节点的插入需要牵涉到树的旋转和变色等操作，这里不再关注其细节部分。

unordered_map

unordered_map是C++11标准中新加入的容器，它的底层是使用hash表的形式来完成映射的功能，在头文件unordered_map中有说明

hash table of {key, mapped} values, unique keys

hash表在底层则是通过hash算法将key的值直接映射到数组上，这样不免会产生hash碰撞的问题，数组的每个单元对应一个bucket，即hash桶，桶可采用链表或是树等多种方式构成。如Java中的HashMap的bucket在1.8更新时就从链表改成了红黑树。

二者的效率对比

二者既然有十分相似的功能，不免会在选择时产生迷茫，到底哪一个数据结构能够满足要求，并且执行的速度又足够快。

实验设计

无序情况下的随机存储查询对比

for (int xx = 1000; xx != 11000; xx += 1000)
	{
		vector t;
		vector ti;
		int b = 0;
		map a;
		for (int n = 0; n != 10000; n++)
		{
			srand(time(nullptr));
			vector key;
			vector val;
			for (int i = 0; i != xx; i++)
			{
				key.emplace_back(rand());
				val.emplace_back(rand());
			}
			LARGE_INTEGER insertstart;
			QueryPerformanceCounter(&insertstart);
			for (int i = 0; i != xx; i++)
			{
				a[key[i]] = val[i];
			}
			LARGE_INTEGER insertend;
			QueryPerformanceCounter(&insertend);
			ti.emplace_back(insertend.QuadPart - insertstart.QuadPart);
			vector find;
			for (int i = 0; i != 10000; i++)
			{
				find.emplace_back(key[rand() % key.size()]);
			}

			LARGE_INTEGER start;
			QueryPerformanceCounter(&start);
			for (auto i :find)
			{
				b += a[i];
			}
			LARGE_INTEGER end;
			QueryPerformanceCounter(&end);
			t.emplace_back(end.QuadPart - start.QuadPart);
			a.clear();
		}
		cout << b << endl;
		LARGE_INTEGER f;
		QueryPerformanceFrequency(&f);
		double avg = static_cast(accumulate(t.begin(), t.end(), 0)) / t.size();
		double avginsert = static_cast(accumulate(ti.begin(), ti.end(), 0)) / ti.size();
		int longestdur = *max_element(t.begin(), t.end());
		int shortestdur = *min_element(t.begin(), t.end());
		cout << "rbt" << xx << endl;
		cout << "avg:" << avg / f.QuadPart * 1000 << " max-min:" << static_cast (longestdur - shortestdur) / avg << endl;
		longestdur = *max_element(ti.begin(), ti.end());
		shortestdur = *min_element(ti.begin(), ti.end());
		cout << "insert time:" << avginsert / f.QuadPart * 1000 <<" max:" << static_cast (longestdur) / f.QuadPart*1000<<" min:"<< static_cast (shortestdur) / f.QuadPart * 1000 << endl;
		double var = 0.0;
		for (auto i : t)
		{
			var += (i - avg)*(i - avg);
		}
		var = var / (t.size() - 1);
		cout << "var:" << var / f.QuadPart * 1000 << endl;
	}

该程序为VC的程序，使用QueryPerformanceCounter来获取执行时间，本次实验使用10000次存n个随机value，取10000个随机key的平均时间作为实验数据，n从1000至10000每1000取一点，从10000至100000每10000取一点。可将map修改为unordered_map来获得unordered_map的结果。

结论

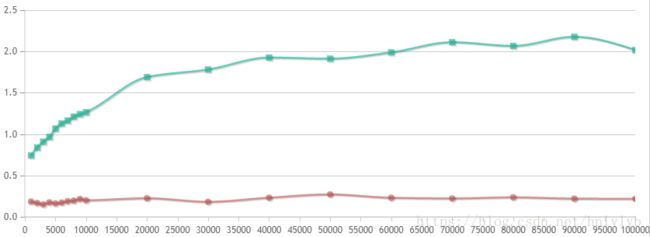
绿线为map的随机访问时间，红线为unordered_map的随机访问时间，可以看出，使用hash表的unordered_map在随机访问上的优势极其明显。与理论值类似，红黑树的随机访问平均时间呈对数状。 

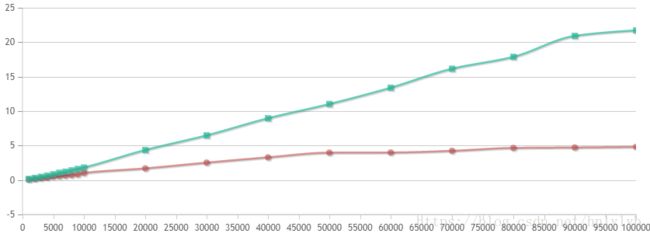
同样的，在插入时间上也有类似的结论，二者的插入时间都呈对数增长，map的时间明显高于 unordered_map。

因此如果在不涉及顺序并且能够设计出较好的hash算法（碰撞较少）的情况下，unordered_map是最好的选择。但是如果考虑顺序的因素，仍旧需要选择map，链表数组等线性结构在排序方面是优于二叉树的，但是当涉及到动态插入的情况时，这些线性结构显得力不从心，以下是在红黑树和链表在排序和动态插入时对比的结果使用的数据为100000个

rbt init time:0.0614347
list init time:0.0227488
rbt insert time:0.0629764
list insert time:60.7506

可以看出，链表排序速度较快，但是有序插入时速度远远低于红黑树，因此在考虑有序的动态数据结构时，红黑树仍旧是较好的选择。