java数据结构与算法之(Queue)队列设计与实现
【版权申明】转载请注明出处(请尊重原创,博主保留追究权)
http://blog.csdn.net/javazejian/article/details/53375004
出自【zejian的博客】
关联文章:
java数据结构与算法之顺序表与链表设计与实现分析
java数据结构与算法之双链表设计与实现
java数据结构与算法之改良顺序表与双链表类似ArrayList和LinkedList(带Iterator迭代器与fast-fail机制)
java数据结构与算法之栈(Stack)设计与实现
java数据结构与算法之队列(Queue)设计与实现
java数据结构与算法之递归思维(让我们更通俗地理解递归)
java数据结构与算法之树基本概念及二叉树(BinaryTree)的设计与实现
java数据结构与算法之平衡二叉查找树(AVL树)的设计与实现
本篇是数据结构与算法的第五篇,本篇我们将来了解一下知识点:
- 队列的抽象数据类型
- 顺序队列的设计与实现
- 链式队列的设计与实现
- 队列应用的简单举例
- 优先队列的设置与实现双链表实现
队列的抽象数据类型
队列同样是一种特殊的线性表,其插入和删除的操作分别在表的两端进行,队列的特点就是先进先出(First In First Out)。我们把向队列中插入元素的过程称为入队(Enqueue),删除元素的过程称为出队(Dequeue)并把允许入队的一端称为队尾,允许出的的一端称为队头,没有任何元素的队列则称为空队。其一般结构如下:
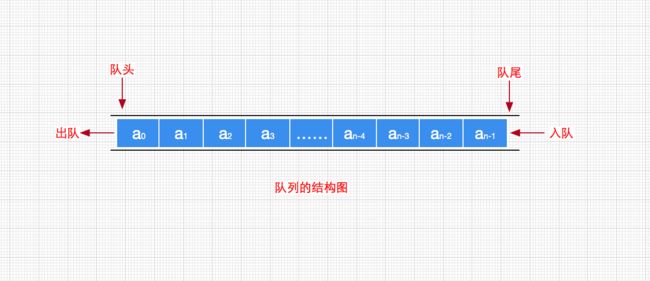
关于队列的操作,我们这里主要实现入队,出队,判断空队列和清空队列等操作,声明队列接口Queue(队列抽象数据类型)如下:
package com.zejian.structures.Queue;
/**
* Created by zejian on 2016/11/28.
* Blog :http://blog.csdn.net/javazejian/article/details/53375004 [原文地址,请尊重原创]
* 队列抽象数据类型
*/
public interface Queue {
/**
* 返回队列长度
* @return
*/
int size();
/**
* 判断队列是否为空
* @return
*/
boolean isEmpty();
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
boolean add(T data);
/**
* offer 方法可插入一个元素,这与add 方法不同,
* 该方法只能通过抛出未经检查的异常使添加元素失败。
* 而不是出现异常的情况,例如在容量固定(有界)的队列中
* NullPointerException:data==null时抛出
* @param data
* @return
*/
boolean offer(T data);
/**
* 返回队头元素,不执行删除操作,若队列为空,返回null
* @return
*/
T peek();
/**
* 返回队头元素,不执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
T element();
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
T poll();
/**
* 出队,执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
T remove();
/**
* 清空队列
*/
void clearQueue();
} 下面我们就来分别实现顺序队列和链式队列
顺序队列的设计与实现
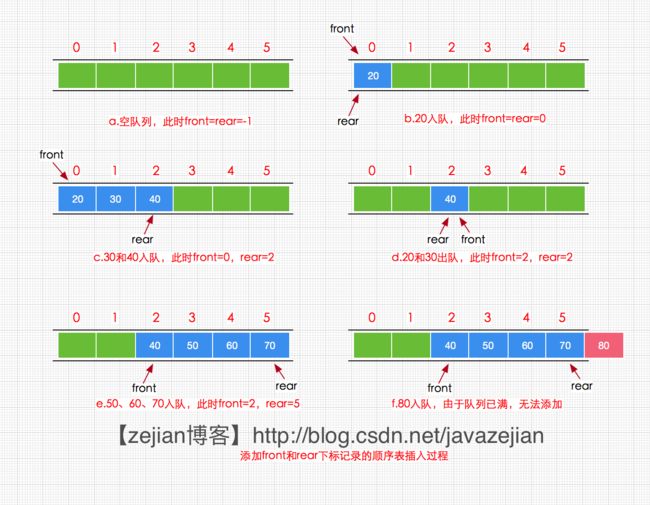
关于顺序队列(底层都是利用数组作为容器)的实现,我们将采用顺序循环队列的结构来实现,在给出实现方案前先来分析一下为什么不直接使用顺序表作为底层容器来实现。实际上采用顺序表实现队列时,入队操作直接执行顺序表尾部插入操作,其时间复杂度为O(1),出队操作直接执行顺序表头部删除操作,其时间复杂度为O(n),主要用于移动元素,效率低,既然如此,我们就把出队的时间复杂度降为O(1)即可,为此在顺序表中添加一个头指向下标front和尾指向下标,出队和入队时只要改变front、rear的下标指向取值即可,此时无需移动元素,因此出队的时间复杂度也就变为O(1)。其过程如下图所示
从图的演示过程,(a)操作时,是空队列此时front和rear都为-1,同时可以发现虽然我们通过给顺序表添加front和rear变量记录下标后使用得出队操作的时间复杂度降为O(1),但是却出现了另外一个严重的问题,那就是空间浪费,从图中的(d)和(e)操作可以发现,20和30出队后,遗留下来的空间并没有被重新利用,反而是空着,所以导致执行(f)操作时,出现队列已满的假现象,这种假现象我们称之为假溢出,之所以出现这样假溢出的现象是因为顺序表队列的存储单元没有重复利用机制,而解决该问题的最合适的方式就是将顺序队列设计为循环结构,接下来我们就通过循环顺序表来实现顺序队列。
顺序循环队列就是将顺序队列设计为在逻辑结构上收尾相接的循环结构,这样我们就可以重复利用存储单元,其过程如下所示:

简单分析一下:
其中采用循环结构的顺序表,可以循环利用存储单元,因此有如下计算关系(其中size为队列长度):
//其中front、rear的下标的取值范围是0~size-1,不会造成假溢出。
front=(front+1)%size;//队头下标
rear=(rear+1)%size;- front为队头元素的下标,rear则指向下一个入队元素的下标
- 当front=rear时,我们约定队列为空。
- 出队操作改变front下标指向,入队操作改变rear下标指向,size代表队列容量。
- 约定队列满的条件为front=(rear+1)%size,注意此时队列中仍有一个空的位置,此处留一个空位主要用于避免与队列空的条件front=rear相同。
- 队列内部的数组可扩容,并按照原来队列的次序复制元素数组
了解了队列的实现规则后,我们重点分析一下入队add方法和出队poll方法,其中入队add方法实现如下:
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
@Override
public boolean add(T data) {
//判断是否满队
if (this.front==(this.rear+1)%this.elementData.length){
ensureCapacity(elementData.length*2+1);
}
//添加data
elementData[this.rear]=data;
//更新rear指向下一个空元素的位置
this.rear=(this.rear+1)%elementData.length;
size++;
return true;
}在add方法中我们先通过this.front==(this.rear+1)%this.elementData.length判断队列是否满,在前面我们约定过队列满的条件为front=(rear+1)%size,如果队列满,则先通过ensureCapacity(elementData.length*2+1)扩容,该方法实现如下:
/**
* 扩容的方法
* @param capacity
*/
public void ensureCapacity(int capacity) {
//如果需要拓展的容量比现在数组的容量还小,则无需扩容
if (capacityreturn;
T[] old = elementData;
elementData= (T[]) new Object[capacity];
int j=0;
//复制元素
for (int i=this.front; i!=this.rear ; i=(i+1)%old.length) {
elementData[j++] = old[i];
}
//恢复front,rear指向
this.front=0;
this.rear=j;
} 这个方法比较简单,主要创建一个新容量的数组,并把旧数组中的元素复制到新的数组中,这里唯一的要注意的是,判断久数组是否复制完成的条件为i!=this.rear,同时循环的自增条件为i=(i+1)%old.length。扩容后直接通过rear添加新元素,最后更新rear指向下一个入队新元素。对于出队操作poll的实现如下:
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
@Override
public T poll() {
T temp=this.elementData[this.front];
this.front=(this.front+1)%this.elementData.length;
size--;
return temp;
}出队操作相对简单些,直接存储要删除元素的数据,并更新队头front的值,最后返回删除元素的数据。ok~,关于循环结构的顺序队列,我们就分析到此,最后给出循环顺序队列的实现源码,其他方法比较简单,注释也很清楚,就不过多分析了:
package com.zejian.structures.Queue;
import java.io.Serializable;
import java.util.NoSuchElementException;
/**
* Created by zejian on 2016/11/28.
* Blog : http://blog.csdn.net/javazejian [原文地址,请尊重原创]
* 顺序队列的实现
*/
public class SeqQueue<T> implements Queue<T> ,Serializable {
private static final long serialVersionUID = -1664818681270068094L;
private static final int DEFAULT_SIZE = 10;
private T elementData[];
private int front,rear;
private int size;
public SeqQueue(){
elementData= (T[]) new Object[DEFAULT_SIZE];
front=rear=0;
}
public SeqQueue(int capacity){
elementData= (T[]) new Object[capacity];
front=rear=0;
}
@Override
public int size() {
// LinkedList
return size;
}
@Override
public boolean isEmpty() {
return front==rear;
}
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
@Override
public boolean add(T data) {
//判断是否满队
if (this.front==(this.rear+1)%this.elementData.length){
ensureCapacity(elementData.length*2+1);
}
//添加data
elementData[this.rear]=data;
//更新rear指向下一个空元素的位置
this.rear=(this.rear+1)%elementData.length;
size++;
return true;
}
/**
* offer 方法可插入一个元素,这与add 方法不同,
* 该方法只能通过抛出未经检查的异常使添加元素失败。
* 而不是出现异常的情况,例如在容量固定(有界)的队列中
* NullPointerException:data==null时抛出
* IllegalArgumentException:队满,使用该方法可以使Queue的容量固定
* @param data
* @return
*/
@Override
public boolean offer(T data) {
if (data==null)
throw new NullPointerException("The data can\'t be null");
//队满抛出异常
if (this.front==(this.rear+1)%this.elementData.length){
throw new IllegalArgumentException("The capacity of SeqQueue has reached its maximum");
}
//添加data
elementData[this.rear]=data;
//更新rear指向下一个空元素的位置
this.rear=(this.rear+1)%elementData.length;
size++;
return true;
}
/**
* 返回队头元素,不执行删除操作,若队列为空,返回null
* @return
*/
@Override
public T peek() {
return elementData[front];
}
/**
* 返回队头元素,不执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T element() {
if(isEmpty()){
throw new NoSuchElementException("The SeqQueue is empty");
}
return peek();
}
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
@Override
public T poll() {
T temp=this.elementData[this.front];
this.front=(this.front+1)%this.elementData.length;
size--;
return temp;
}
/**
* 出队,执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T remove() {
if (isEmpty()){
throw new NoSuchElementException("The SeqQueue is empty");
}
return poll();
}
@Override
public void clearQueue() {
for (int i=this.front; i!=this.rear ; i=(i+1)%elementData.length) {
elementData[i] = null;
}
//复位
this.front=this.rear=0;
size=0;
}
/**
* 扩容的方法
* @param capacity
*/
public void ensureCapacity(int capacity) {
//如果需要拓展的容量比现在数组的容量还小,则无需扩容
if (capacityreturn;
T[] old = elementData;
elementData= (T[]) new Object[capacity];
int j=0;
//复制元素
for (int i=this.front; i!=this.rear ; i=(i+1)%old.length) {
elementData[j++] = old[i];
}
//恢复front,rear指向
this.front=0;
this.rear=j;
}
} 链式队列的设计与实现
分析完顺序队列,我们接着看看链式队列的设计与实现,对于链式队列,将使用带头指针front和尾指针rear的单链表实现,front直接指向队头的第一个元素,rear指向队尾的最后一个元素,其结构如下:
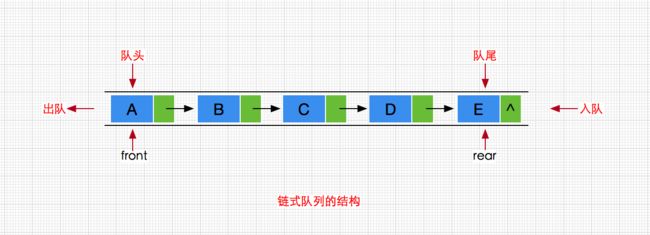
之所以选择单链表(带头尾指针)而不采用循环双链表或者双链表主要是双链表的空间开销(空间复杂度,多前继指针)相对单链表来说大了不少,而单链表只要新增头指针和尾指针就可以轻松实现常数时间内(时间复杂度为O(1))访问头尾结点。下面我们来看看如何设计链式队列:
- 以上述的图为例分别设置front和rear指向队头结点和队尾结点,使用单链表的头尾访问时间复杂度为O(1)。
- 设置初始化空队列,使用front=rear=null,并且约定条件
front==null&&rear==null成立时,队列为空。 - 出队操作时,若队列不为空获取队头结点元素,并删除队头结点元素,更新front指针的指向为front=front.next
- 入队操作时,使插入元素的结点在rear之后并更新rear指针指向新插入元素。
- 当第一个元素入队或者最后一个元素出队时,同时更新front指针和rear指针的指向。
这一系列过程如下图所示:
ok~,关于链式队列的设计都分析完,至于实现就比较简单了,和之前分析过的单链表区别不大,因此这里我们直接给出实现代码即可:
package com.zejian.structures.Queue;
import com.zejian.structures.LinkedList.singleLinked.Node;
import java.io.Serializable;
import java.util.*;
/**
* Created by zejian on 2016/11/28.
* Blog : http://blog.csdn.net/javazejian/article/details/53375004 [原文地址,请尊重原创]
* 链式队列的实现
*/
public class LinkedQueue<T> implements Queue<T> ,Serializable{
private static final long serialVersionUID = 1406881264853111039L;
/**
* 指向队头和队尾的结点
* front==null&&rear==null时,队列为空
*/
private Node front,rear;
private int size;
/**
* 用于控制最大容量,默认128,offer方法使用
*/
private int maxSize=128;
public LinkedQueue(){
//初始化队列
this.front=this.rear=null;
}
@Override
public int size() {
return size;
}
public void setMaxSize(int maxSize){
this.maxSize=maxSize;
}
@Override
public boolean isEmpty() {
return front==null&&rear==null;
}
/**
* data 入队,添加成功返回true,否则返回false,可扩容
* @param data
* @return
*/
@Override
public boolean add(T data) {
Node q=new Node<>(data,null);
if (this.front==null) {//空队列插入
this.front = q;
} else {//非空队列,尾部插入
this.rear.next=q;
}
this.rear=q;
size++;
return true;
}
/**
* offer 方法可插入一个元素,这与add 方法不同,
* 该方法只能通过抛出未经检查的异常使添加元素失败。
* 而不是出现异常的情况,例如在容量固定(有界)的队列中
* NullPointerException:data==null时抛出
* IllegalArgumentException:队满,使用该方法可以使Queue的容量固定
* @param data
* @return
*/
@Override
public boolean offer(T data) {
if (data==null)
throw new NullPointerException("The data can\'t be null");
if (size>=maxSize)
throw new IllegalArgumentException("The capacity of LinkedQueue has reached its maxSize:128");
Node q=new Node<>(data,null);
if (this.front==null) {//空队列插入
this.front = q;
} else {//非空队列,尾部插入
this.rear.next=q;
}
this.rear=q;
size++;
return false;
}
/**
* 返回队头元素,不执行删除操作,若队列为空,返回null
* @return
*/
@Override
public T peek() {
return this.isEmpty()? null:this.front.data;
}
/**
* 返回队头元素,不执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T element() {
if(isEmpty()){
throw new NoSuchElementException("The LinkedQueue is empty");
}
return this.front.data;
}
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
@Override
public T poll() {
if (this.isEmpty())
return null;
T x=this.front.data;
this.front=this.front.next;
if (this.front==null)
this.rear=null;
size--;
return x;
}
/**
* 出队,执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T remove() {
if (isEmpty()){
throw new NoSuchElementException("The LinkedQueue is empty");
}
T x=this.front.data;
this.front=this.front.next;
if (this.front==null)
this.rear=null;
size--;
return x;
}
@Override
public void clearQueue() {
this.front= this.rear=null;
size=0;
}
} 队列应用的简单举例
- 模拟现实世界中的队列,如售票柜台的队列以及其他先到先服务的场景。
- 计算客户在呼叫中心等待的时间。
- 异步数据的传输(文件输入输出、管道、嵌套字)。
- 操作系统中的优先级任务执行。
- 短信群体发送 应用的发布订阅模式
优先队列的设置与实现(双链表实现)
了解完循环顺序队列和链式队列的实现后,我们最后再来了解一个特殊的队列,也就是优先队列,在某些情况下,有些应用系统要求不仅需要按照“先来先服务”的原则进行,而且还需按照任务的重要或紧急程度进行排队处理,此时就需要使用到优先队列。比如在操作系统中进行进程调度管理,每个进程都具备一个优先级值以表示进程的紧急程度,优先级高的进行先执行,同等级进程按照先进先出的原则排队处理,此时操作系统使用的便是优先队列管理和调度进程。
优先级队列也是一种特殊的数据结构,队列中的每个元素都有一个优先级,若每次出队的是具有最高优先级的元素,则称为降序优先级队列(总是先删除最大的元素)。若每次出队的是值最小的元素,则称为升序优先级队列(总是先删除最小的元素),通常情况下我们所说的优先队列,一般是指降序优先级队列。关于优先队列的实现,可以使用有序数组或者有序链表,也可以使用二叉树(二叉堆)实现,这里我们仅给出有序链表的简单实现方案。而二叉树的实现,留着后面我们分析完树时再给出。好~,这里使用之前分析过的MyLikedList作为基底,实现一个排序的SortLinkedList继承自MyLinkedList,这里需要注意的是排序链表中的T类型必须是实现了Comparable接口的类型,在SortLinkedList中主要重写添加的add方法,插入逻辑是,通过比较元素的大小加入,而非简单下标或尾部插入,其实现如下:
package com.zejian.structures.LinkedList.MyCollection;
import java.io.Serializable;
import java.util.Iterator;
import java.util.ListIterator;
/**
* Created by zejian on 2016/12/3.
* Blog : http://blog.csdn.net/javazejian [原文地址,请尊重原创]
* 排序list的简单实现
*/
public class SortMyLinkedList<T extends Comparableextends T>> extends MylinkeList<T> implements Serializable {
private static final long serialVersionUID = -4783131709270334156L;
@Override
public boolean add(T data) {
if(data==null)
throw new NullPointerException("data can\'t be null");
Comparable cmp =data;//这里需要转一下类型,否则idea编辑器上检验不通过.
if(this.isEmpty() || cmp.compareTo(this.last.prev.data) > 0){
return super.add(data);//直接尾部添加,last不带数据的尾结点
}
Node p=this.first.next;
//查找插入点
while (p!=null&&cmp.compareTo(p.data)>0)
p=p.next;
Node q=new Node<>(p.prev,data,p);
p.prev.next=q;
p.prev=q;
size++;
//记录修改
modCount++;
return true;
}
/**
* 不根据下标插入,只根据比较大小插入
* @param index
* @param data
*/
@Override
public void add(int index, T data) {
this.add(data);
}
/**
* 未实现
* @param index
* @return
*/
@Override
public ListIterator listIterator(int index) {
return null;
}
/**
* 未实现
* @return
*/
@Override
public Iterator iterator() {
return null;
}
//测试
public static void main(String[] args){
SortMyLinkedList list=new SortMyLinkedList<>();
list.add(50);
list.add(40);
list.add(80);
list.add(20);
print(list);
}
public static void print(SortMyLinkedList mylinkeList){
for (int i=0;i"i->"+mylinkeList.get(i));
}
}
} 接着以SortMyLinkedList为基底实现优先队列PriorityQueue,实现源码如下,实现比较简单,感觉没啥好说的:
package com.zejian.structures.Queue;
import com.zejian.structures.LinkedList.MyCollection.SortMyLinkedList;
import java.io.Serializable;
import java.util.NoSuchElementException;
/**
* Created by zejian on 2016/11/30.
* Blog : http://blog.csdn.net/javazejian [原文地址,请尊重原创]
* 优先队列的简单实现,采用排序双链表,T必须实现Comparable接口
*/
public class PriorityQueue<T extends Comparableextends T>> implements Queue<T> ,Serializable {
private static final long serialVersionUID = 8050142086009260625L;
private SortMyLinkedList list;//排序循环双链表
private boolean asc;//true表示升序,false表示降序
/**
* 用于控制最大容量,默认128,offer方法使用
*/
private int maxSize=128;
/**
* 初始化队列
* @param asc
*/
public PriorityQueue(boolean asc){
this.list=new SortMyLinkedList<>();
this.asc=asc;//默认升序
}
public int getMaxSize() {
return maxSize;
}
public void setMaxSize(int maxSize) {
this.maxSize = maxSize;
}
@Override
public int size() {
return list.size();
}
@Override
public boolean isEmpty() {
return list.isEmpty();
}
/**
* data 入队,添加成功返回true,否则返回false
* @param data
* @return
*/
@Override
public boolean add(T data) {
return list.add(data);
}
/**
* offer 方法可插入一个元素,这与add 方法不同,
* 该方法只能通过抛出未经检查的异常使添加元素失败。
* 而不是出现异常的情况,例如在容量固定(有界)的队列中
* NullPointerException:data==null时抛出
* IllegalArgumentException:队满,使用该方法可以使Queue的容量固定
* @param data
* @return
*/
@Override
public boolean offer(T data) {
if (data==null)
throw new NullPointerException("The data can\'t be null");
if (list.size()>=maxSize)
throw new IllegalArgumentException("The capacity of PriorityQueue has reached its maxSize:128");
return add(data);
}
/**
* 返回队头元素,不执行删除操作,若队列为空,返回null
* @return
*/
@Override
public T peek() {
if(isEmpty()){
return null;
}
return this.asc ? this.list.get(0):this.list.get(size()-1);
}
/**
* 返回队头元素,不执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T element() {
if(isEmpty()){
throw new NoSuchElementException("The PriorityQueue is empty");
}
return peek();
}
/**
* 出队,执行删除操作,返回队头元素,若队列为空,返回null
* @return
*/
@Override
public T poll() {
if(isEmpty()){
return null;
}
return this.asc ? this.list.remove(0): this.list.remove(list.size()-1);
}
/**
* 出队,执行删除操作,若队列为空,抛出异常:NoSuchElementException
* @return
*/
@Override
public T remove() {
if (isEmpty()){
throw new NoSuchElementException("The PriorityQueue is empty");
}
return poll();
}
@Override
public void clearQueue() {
this.list.clear();
}
//测试
public static void main(String[] args){
PriorityQueue priorityQueue=new PriorityQueue<>(false);
System.out.println("初始化队列");
priorityQueue.add(new Process("进程1",10));
priorityQueue.add(new Process("进程2",1));
priorityQueue.add(new Process("进程3",8));
priorityQueue.add(new Process("进程4",3));
priorityQueue.add(new Process("进程5"));
System.out.println("队列中的进程执行优先级:");
while (!priorityQueue.isEmpty()){
System.out.println("process:"+priorityQueue.poll().toString());
}
}
} ok~,就到这吧,下一篇我们聊聊递归算法,源码下载地址:
github源码下载(含文章列表,持续更新)