第一阶段-入门详细图文讲解tensorflow1.4 -（十一）TensorBoard Histogram Dashboard

TensorBoard直方图仪表板显示TensorFlow图中某些张量的分布随时间如何变化。 它通过在不同的时间点显示张量的许多直方图可视化。

一，看一个基础例子

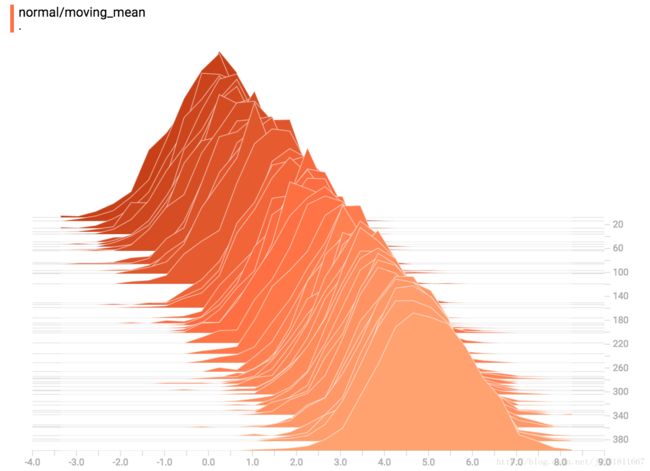
a normally-distributed variable,一个正态分布值。mean随着时间的变化。
我们直接使用tf.random_normal操作。完美解决。
当然，还要使用TensorBoard，summary操作填充数据。代码片段。

import tensorflow as tf

k = tf.placeholder(tf.float32)

# 生成一个正态分布, 并且改变正态分布的中值mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# 记录这个分布为直方图摘要
tf.summary.histogram("normal/moving_mean", mean_moving_normal)

# 设置一个session，并且写出summary 的events files
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")

summaries = tf.summary.merge_all()

# 设置一个400循环，并将这些summary写入硬盘
N = 400
for step in range(N):
  k_val = step/float(N)
  summ = sess.run(summaries, feed_dict={k: k_val})
  writer.add_summary(summ, global_step=step)

使用一下命令启动一个TensorBoard实例。

tensorboard --logdir=D:\tmp\histogram_example

此外，您可能会注意到，直方图切片并不总是以步骤计数或时间间隔均匀分布。 这是因为TensorBoard使用池采样来保留所有直方图的一个子集，以节省内存。(Reservoir sampling guarantees) 池采样保证每个样本都有相同的被包含的可能性，但是因为它是一个随机算法，选择的样本不会在偶数步中发生。

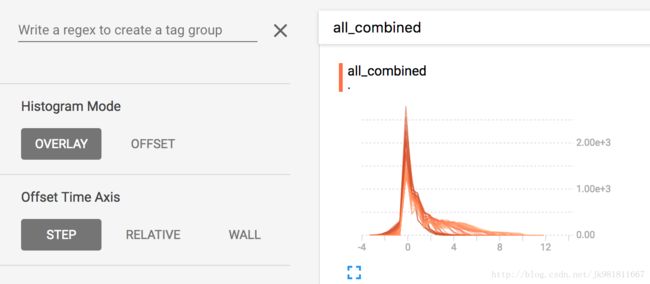
二，Overlay Mode（覆盖模式）

Histogram Mode中选择overly mode

在“offset”模式下，可视化旋转45度，以便各个直方图切片不再及时展开，而是全部绘制在相同的y轴上。

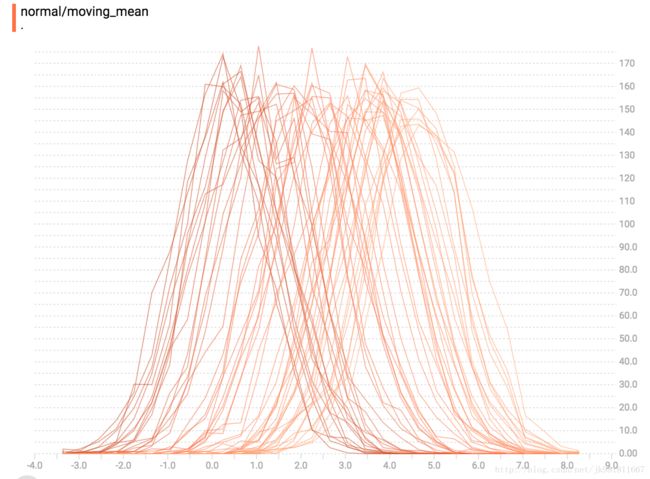
现在，每个切片在图表上都是单独的一行，y轴显示每个存储桶内的项目数。 较深的线条较旧，较早的步骤较轻，较浅的线条较近。 再次，您可以将鼠标悬停在图表上以查看一些其他信息。

In general, the overlay visualization is useful if you want to directly compare the counts of different histograms.
通常情况下，覆盖模式应用于直接对比不同的直方图。

三，Multimodal Distributions（多模型分布）

直方图仪表板非常适合可视化多模式分布。 让我们通过连接两个不同的正态分布的输出来构造一个简单的双峰分布。 代码将如下所示。

import tensorflow as tf

k = tf.placeholder(tf.float32)

# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)

# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)

# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)

summaries = tf.summary.merge_all()

# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")

# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
  k_val = step/float(N)
  summ = sess.run(summaries, feed_dict={k: k_val})
  writer.add_summary(summ, global_step=step)

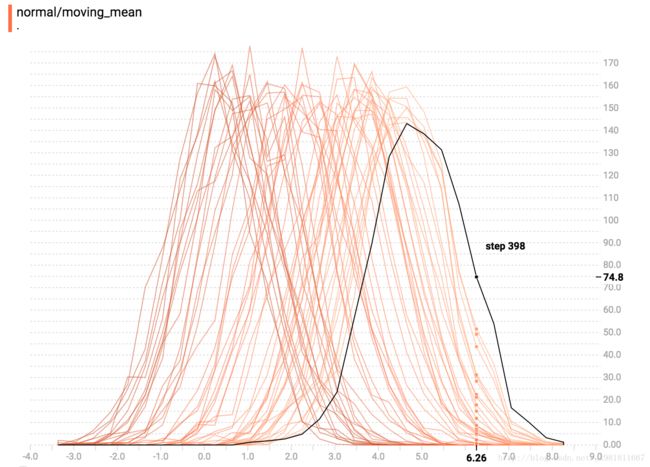
你已经记得上面例子中的“移动均值”正态分布。 现在我们也有一个“收缩差异”的分布。 并排，他们看起来像这样：

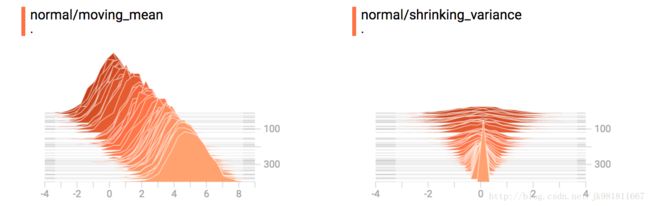
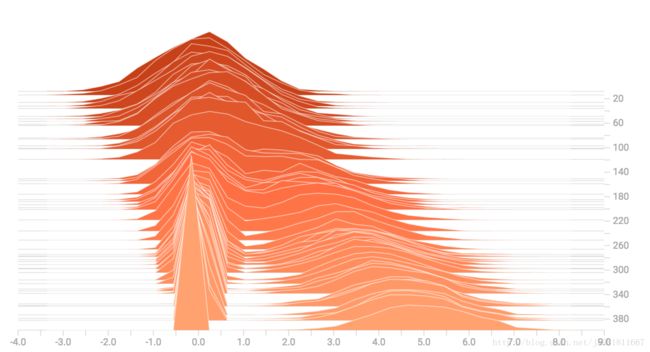
当我们把它们连接起来的时候，我们得到一个清楚地显示出不同的双峰结构的图表：

四，Some more distributions（更多的分布）

很有趣，让我们生成和可视化更多的分布，然后将它们合并成一个图表。 以下是我们将使用的代码：

import tensorflow as tf

k = tf.placeholder(tf.float32)

# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)

# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)

# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)

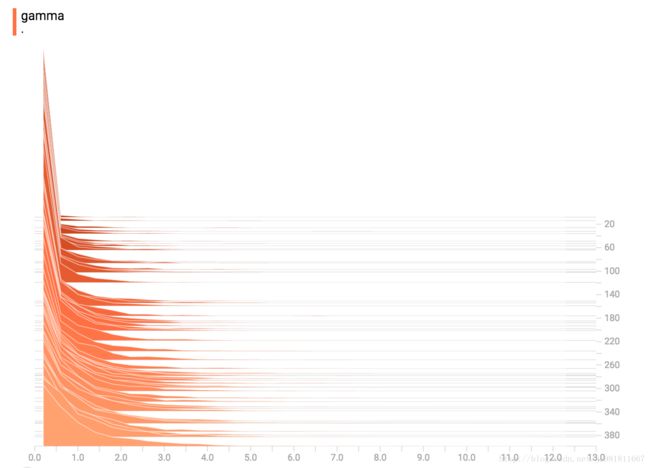
# Add a gamma distribution
gamma = tf.random_gamma(shape=[1000], alpha=k)
tf.summary.histogram("gamma", gamma)

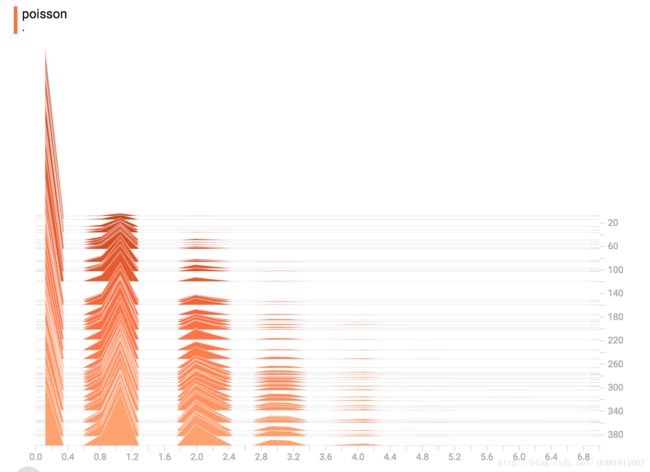
# And a poisson distribution
poisson = tf.random_poisson(shape=[1000], lam=k)
tf.summary.histogram("poisson", poisson)

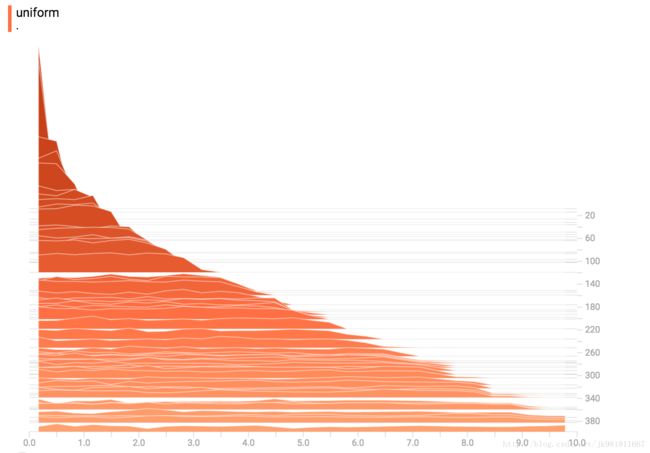
# And a uniform distribution
uniform = tf.random_uniform(shape=[1000], maxval=k*10)
tf.summary.histogram("uniform", uniform)

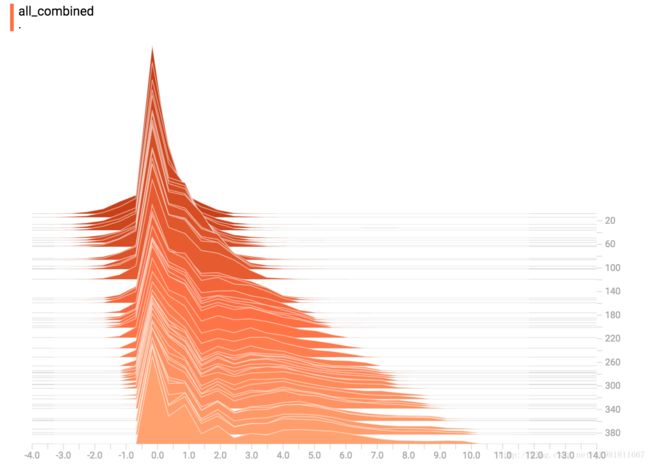
# Finally, combine everything together!
all_distributions = [mean_moving_normal, variance_shrinking_normal,
                     gamma, poisson, uniform]
all_combined = tf.concat(all_distributions, 0)
tf.summary.histogram("all_combined", all_combined)

summaries = tf.summary.merge_all()

# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")

# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
  k_val = step/float(N)
  summ = sess.run(summaries, feed_dict={k: k_val})
  writer.add_summary(summ, global_step=step)

Gamma Distribution

Uniform Distribution

Poisson Distribution

泊松分布是在整数上定义的。 所以，所有生成的值都是完美的整数。 直方图压缩将数据移动到浮点数据库，导致可视化文件在整数值上显示出很小的颠簸，而不是完美的尖峰。

All Together Now

最后，我们可以将所有的数据连接成一个有趣的曲线。

blog结束。