（深度学习）AI换脸？——Pytorch实现GAN、WGAN、WGAN-GP

（深度学习）AI换脸？——Pytorch实现GAN、WGAN、WGAN-GP

GAN

WGAN

WGAN-GP

详细代码

此文为Pytorch深度学习的第四篇文章，在上一篇文章中（深度学习）Pytorch自己动手不调库实现LSTM我们不调库手动实现了LSTM。今天我们放松一下，来实现AI换脸(一看就是P站老流氓了 )中常常用到的GAN、WGAN、WGAN-GP这三个模型。

GAN

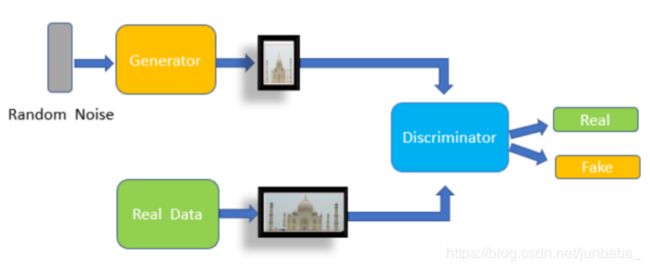
GAN（Generative Adversarial Networks）是一种深度学习模型，是由Ian J. Goodfellow等人于2014年10月在Generative Adversarial Networks中所提出的一个通过对抗过程估计生成模型的新框架。模型主要由两个模块构成，分别为判别器(discriminator)与生成器(generator)，如下图所示。其中，判别器判断一个样本是真实样本还是生成器生成样本；生成器生成样本，并尽量让判别器无法判断是否是生成的。

在优化过程中，我们首先要使判别器尽可能分离两种样本；同时，也要生成器样本无法被识别。因此，我们的损失函数需要使用如下式所示的maxmin算法。这是一个对抗的过程，max使得判别器尽可能分离两种样本、min使得生成器样本无法被识别。
$$\underset{G}{\min }\underset{D}{\max }V\{D,G\}=E_{x\sim P_{data}(x)}[logD(x)]+E_{z\sim p_z(z)}[log(1-D(G(z)))]$$
GAN模型主要由两部分构成，分别是生成器模型Generator和判别器模型Discriminator，二者都是由深度神经网络构成，与先前的MLP类似，故不赘述。判别器模型前向传播过程中最后需要加上sigmoid函数，结合nn.BCELoss()得到损失函数。

class Generator(nn.Module):
    """
    个人构造的生成器模型
    """

    def __init__(self, noise_size, g_middle_size, g_output_size):
        super(Generator, self).__init__()
        self.gen = nn.Sequential(
            nn.Linear(noise_size, g_middle_size),
            nn.ReLU(True),
            nn.Linear(g_middle_size, g_middle_size),
            nn.ReLU(True),
            nn.Linear(g_middle_size, g_middle_size),
            nn.ReLU(True),
            nn.Linear(g_middle_size, g_output_size),
        )

    def forward(self, x):
        output = self.gen(x)
        return output


class Discriminator(nn.Module):
    """
    个人构造的判别器模型
    """

    def __init__(self, g_output_size, d_middle_size, wgan=False):
        super(Discriminator, self).__init__()
        self.wgan = wgan
        self.disc = nn.Sequential(
            nn.Linear(g_output_size, d_middle_size),
            nn.ReLU(True),
            nn.Linear(d_middle_size, d_middle_size),
            nn.ReLU(True),
            nn.Linear(d_middle_size, d_middle_size),
            nn.ReLU(True),
            nn.Linear(d_middle_size, 1),    # 最后输出一维，判断是或否
        )
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        output = self.disc(x)
        # WGAN与GAN的主要区别在于WGAN去掉了最后一层的sigmoid函数
        if not self.wgan:
            output = self.sigmoid(output)
        return output

在训练过程中，如下面代码所示，我使用了maxmin算法，首先要进行maxmin算法的maximize判别器Loss的部分，接着进行maxmin算法的minimize生成器Loss的部分。另外，在下列代码中也包含了WGAN与WGAN-GP的训练过程。

"""
首先要进行maxmin算法的maximize判别器Loss的部分
"""
# WGAN需要将判别器的参数绝对值截断到不超过一个固定常数c
if opt.model == 'wgan':
    for p in disc_net.parameters():
        p.data.clamp_(opt.clamp_lower, opt.clamp_upper)
disc_net.zero_grad()

# 优化过程根据GAN、WGAN、WGAN-GP三种模型的不同而异。另外，为了能和之前求最小值的优化过程一致，这里我们选用损失值的相反数作为优化目标，即
# maximize A <==> min -A
if opt.model == 'wgan':
    # WGAN相较于GAN，判别器最后一层去掉sigmoid函数，故直接求期望即可，不必使用损失函数
    D_Loss_real = disc_net(real_img).mean()
    fake = gen_net(noise)
    D_Loss_fake = disc_net(fake).mean()
    D_Loss = -(D_Loss_real - D_Loss_fake)
    # 反向传播
    D_Loss.backward()
elif opt.model == 'wgan-gp':
    # WGAN-GP此处与WGAN同
    D_Loss_real = disc_net(real_img).mean()
    fake = gen_net(noise)
    D_Loss_fake = disc_net(fake).mean()
    # WGAN-GP相较于WGAN引入了gradient penalty限制梯度
    gradient_penalty = cal_gradient_penalty(disc_net, device, real_img.data, fake.data)
    D_Loss = -(D_Loss_real - D_Loss_fake) + gradient_penalty * 0.1
    # 反向传播
    D_Loss.backward()
else:
    # 与上面两个不同的是，GAN的公式是maximize log(D(x)) + log(1 - D(G(z)))
    D_Loss_real = criterion(disc_net(real_img), reallabel)
    fake = gen_net(noise)
    D_Loss_fake = criterion(disc_net(fake.detach()), fakelabel)
    D_Loss = D_Loss_real + D_Loss_fake
    # 反向传播
    D_Loss.backward()
D_epochloss += D_Loss.item()
# 优化
optimizer_D.step()

"""
接着要进行maxmin算法的minimize生成器Loss的部分
"""
# 将梯度缓存置0
gen_net.zero_grad()
# 生成放入generator中的噪声
noise = torch.randn(batch_size, opt.noise_size).to(device)
fake = gen_net(noise)
# 分模型的细节与上述原理相同
if opt.model == 'wgan':
    G_Loss = -disc_net(fake).mean()
    G_Loss.backward()
elif opt.model == 'wgan-gp':
    G_Loss = -disc_net(fake).mean()
    G_Loss.backward()
else:
    G_Loss = criterion(disc_net(fake), reallabel)
    G_Loss.backward()
G_epochloss += G_Loss.item()
optimizer_G.step()

WGAN

GAN模型存在两点不合理的地方：

• 生成器初始化的分布与真实分布重叠部分测度为0的概率为1，导致第一个生成器版本的梯度消失。
• 等价优化目标存在不合理的距离度量。

为了解决这两个问题，WGAN被提出。相较于GAN，WGAN做出了如下改进：

• 判别器最后一层去掉sigmoid。
• 生成器和判别器中的loss不取对数。
• 每次更新判别器的参数，将他们的绝对值截断到不超过一个固定常数c。
• 不用基于动量的优化算法(momentum Adam)。

在代码实现中，首先WGAN去掉了最后一层的sigmoid函数：

def forward(self, x):
    output = self.disc(x)
    # WGAN与GAN的主要区别在于WGAN去掉了最后一层的sigmoid函数
    if not self.wgan:
        output = self.sigmoid(output)
    return output

训练过程中，不使用nn.BCELoss()，且每次WGAN都需要将判别器的参数绝对值截断到不超过一个固定常数c：

if opt.model == 'wgan':
    # WGAN相较于GAN，判别器最后一层去掉sigmoid函数，故直接求期望即可，不必使用损失函数
    D_Loss_real = disc_net(real_img).mean()
    fake = gen_net(noise)
    D_Loss_fake = disc_net(fake).mean()
    D_Loss = -(D_Loss_real - D_Loss_fake)
    # 反向传播
    D_Loss.backward()

# WGAN需要将判别器的参数绝对值截断到不超过一个固定常数c
if opt.model == 'wgan':
    for p in disc_net.parameters():
        p.data.clamp_(opt.clamp_lower, opt.clamp_upper)
disc_net.zero_grad()

WGAN-GP

WGAN中的weight clipping的实现方式存在两个严重的问题:

• 判别器的loss希望尽可能拉大真假样本的分数差,实验发现基本上最终权重集中在两端,这样参数的多样性减少,会使判别器得到的神经网络学习一个简单的映射函数,是巨大的浪费.
• 很容易导致梯度消失或者梯度爆炸,若把clipping threshold设的较小,每经过一个网络,梯度就会变小,多级之后会成为指数衰减;反之,较大,则会使得指数爆炸.这个平衡区域可能很小。

为了解决这个问题，WGAN-GP被提出。WGAN-GP引入了gradient penalty，并将其与WGAN的判别器Loss函数相加构成新的Loss函数：
$$L(D)=-E_{x\sim P_{data}}[D(x)]+E_{x\sim p_g}[D(x)]+\lambda E_{x\sim \chi }[||{\nabla }_{x}D(x)|{|}_p-1{]}^2$$
在代码实现中，首先如下列代码所示，我定义了计算gradient penalty的函数。首先计算系数，进而计算梯度，最后利用梯度计算出gradient penalty：

def cal_gradient_penalty(disc_net, device, real, fake):
    """
    用于计算WGAN-GP引入的gradient penalty
    """
    # 系数alpha
    alpha = torch.rand(real.size(0), 1)
    alpha = alpha.expand(real.size())
    alpha = alpha.to(device)

    # 按公式计算x
    interpolates = alpha * real + ((1 - alpha) * fake)

    # 为得到梯度先计算y
    interpolates = autograd.Variable(interpolates, requires_grad=True)
    disc_interpolates = disc_net(interpolates)

    # 计算梯度
    gradients = autograd.grad(outputs=disc_interpolates, inputs=interpolates,
                              grad_outputs=torch.ones(disc_interpolates.size()).to(device),
                              create_graph=True, retain_graph=True, only_inputs=True)[0]

    # 利用梯度计算出gradient penalty
    gradient_penalty = ((gradients.norm(2, dim=1) - 1) ** 2).mean()
    return gradient_penalty

另外，在判别器Loss函数上按照公式加上了乘以系数的gradient penalty：

elif opt.model == 'wgan-gp':
    # WGAN-GP此处与WGAN同
    D_Loss_real = disc_net(real_img).mean()
    fake = gen_net(noise)
    D_Loss_fake = disc_net(fake).mean()
    # WGAN-GP相较于WGAN引入了gradient penalty限制梯度
    gradient_penalty = cal_gradient_penalty(disc_net, device, real_img.data, fake.data)
    D_Loss = -(D_Loss_real - D_Loss_fake) + gradient_penalty * 0.1
    # 反向传播
    D_Loss.backward()

详细代码

详细代码可见：详细代码

原创不易，求赞求github打星。