目前看的GNN论文的一些总结
该文首发于知乎专栏:在天大的日日夜夜 已获得作者授权
最近组会轮到我讲了,打算讲一下目前看的一些GNN论文以及该方向的一些重要思想,其中有借鉴论文[1]、[2]的一些观点和《深入浅出图神经网络:GNN原理解析》一书中的观点。其中可能有一些不准确和不全面的地方,欢迎大家指出。
1.为什么我们需要图神经网络:
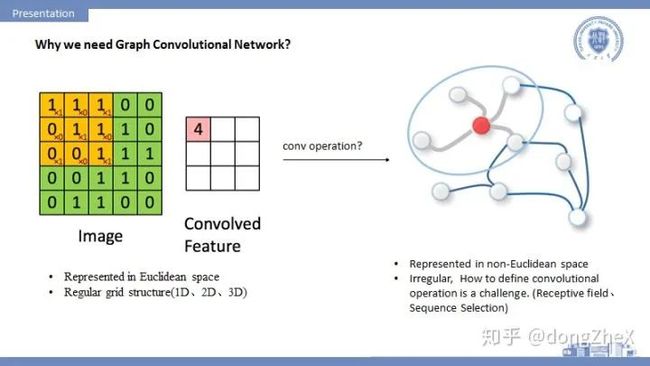 图 1
图 1
当前,深度学习技术已经在语音识别、机器翻译、图像分析和计算机视觉等方向取得了重要成果,之所以CNN、RNN等模型能够在图像、音频等处理中取得很好地效果,其一个重要原因是:图像、音频等数据都可以很好地在欧式空间中进行表示,并且以规则的栅栏结构呈现,CNN等可以很自然的在这些数据上进行操作。
而也有很多数据,如社交网络数据、生物化学图结构和引文网络等,这些只能在非欧空间中表示,图(Graph)是其中一个典型的表示方式。
图结构数据的表示一般是不规则,传统的CNN等模型无法直接运用在图数据上,所以需要在图上重新定义卷积操作。其中要着重考虑感受野如何定义,节点的顺序性如何定义,如何进行池化操作等等,这方面大家可以参考论文论文[3],其中有比较详细的讨论。
2.图神经网络发展的一些历史
 图 2
图 2
①最早的图神经网络是Network Embedding的形式,它的核心思想是通过表征学习的方式,在保持当前空间一些几何特性的前提下,把数据转换到一个低维的、更加有判别能力的空间。常见的方法有LLE、DeepWalk、SNE、Graph Factorization等方法。更多可以参考,这篇知乎(谢谢该作者):
苏一:图嵌入(Graph embedding)综述 zhuanlan.zhihu.com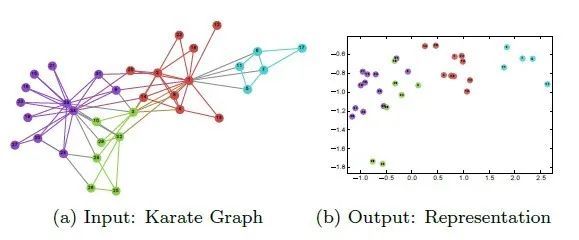
这方面强烈建议看一下DeepWalk这篇论文,是network embedding中非常重的一篇论文,该方法借鉴NLP的思想,使用random walk和SkipGram来提取社交网络数据中的结构信息。
这些方法的通病是对那些拥有节点特征的数据不感冒,有些方法加入节点特征的处理,但其实效果都不是特别好。
②在之后出现了Recurrent graph neural networks,这种方法的主要思想是假设一个节点不断地与邻居节点交换信息直到达到一个平衡,其大多借鉴了LSTM、GRU这些RNN模型,然后改进并运用到 图数据上,这方面我没有具体看过论文。大家如果有兴趣可以参考论文[1],然后再去查看相关论文。
③在2013年nips上,论文[4]提出使用图信号处理技术来定义谱图卷积,其核心思想是通过图傅里叶变换将图信号从空间域转换到频域,进而在频域上定义图卷积操作,其具体操作可以可以参考这篇知乎:
如何理解 Graph Convolutional Network(GCN)? www.zhihu.com
我们直接看结果:
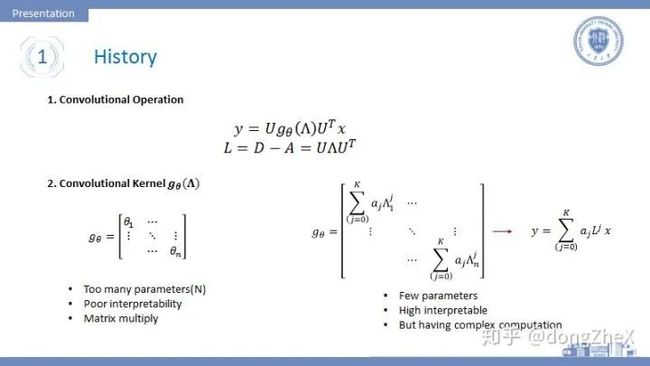 图 3
图 3
图 3 上方的第一行式子就是对图数据x进行的谱图卷积操作,其中U代表拉普拉斯矩阵的特征向量,Lambda表示拉普拉斯矩阵的特征值矩阵,拉普拉斯矩阵是对称矩阵,所以他一定可以进行对角化。
表示图卷积的卷积核,最初始的卷积核定义有两种形式
第一种为图3左下角形式为一个拥有N(节点数)个参数的对角阵,这种形式比较简单,但是会遇到几个问题:(i)参数数量与图节点数量挂钩,在处理大图时会产生参数过多的问题(ii)解释性极差;(iii)需要计算特征向量,并进行多次矩阵乘法,计算复杂度高。
为了解决1中的问题,提出了第二种图3右下角的形式,这种形式看似复杂,但是可以通过对角化性质进行化简成:

这是式子中,对于每个K只有一个参数,L的j次幂可以表示节点的j阶连通性,这也带来了较好的解释性:中心节点聚合其K阶邻居的信息,所以K可以理解为感受野,且参数数量等于K(一般K很小,例如K=2)。但是这个卷积核形式带来一些问题如:需要计算L的幂,造成了较高的计算复杂度。
自此GNN变得可以一边提取结构特征、一边提取节点特征。
3. Basic Model
 图 4
图 4
论文[5]提出了ChebNet(图4左侧),该模型对于图卷积的改进在于使用切比雪夫多项式来近似计算拉普拉斯矩阵的幂运算,原来的幂运算可以通过递归的形式来求得,简化了运算。
论文[6]是图卷积领域一篇非常经典的论文,将图卷积应用于半监督学习中。我们这里不讨论其半监督学习的方法。该论文在论文[5]的基础上进行了一阶近似,即每次卷积操作只对节点的一阶邻居进行信息聚合,并且省略了部分参数。除此之外,作者在层与层之间加入了线性变化矩阵和激活函数的操作,并使用softmax和交叉熵损失完成节点分类任务。图4右侧展示了模型的核心计算公式,可以看到卷积核几乎消失了。论文[1]中也因此称该论文为连接谱图卷积和空间域卷积的桥梁。除此之外,该式中的 为经过标准化和增加自连接的拉普拉斯矩阵,可以起到稳定计算的作用。具体细节可以查询具体论文。
值得一提的是,从半监督的角度来看这篇论文,也可以解释为使用图卷积提取结构信息来达到使用少量标签数据完成节点分类任务的目的。但是这篇论文在半监督上做的并不是特别好,我在做实验的时候发现模型对于标签数据的依赖性还是很大的,当减少训练集的标签数据时,模型效果会明显的下降。所以现在半监督领域有许多改进CN的工作,想办法用更少的标签来训练GCN,这些论文一个通常的特征就是做实验的时候会摆出训练集的分割比。
目前提到的方法存在着很多问题:
无法进行分批训练,其原因是的存在,无法对分批的数据完成运算,这也对应了该方法的灵活性差,无法处理大图。
模型基于transductive,即在训练过程中,测试集的数据也有参与,这造成模型的泛化能力很差。
无法通过加深网络层数来加强网络,这是GNN领域的一个重要问题。Shallow or Deep?这方面在文末会顺带一提,相关论文也非常之多。
基于以上前两个两个比较致命的缺点,研究者使用空间域卷积来解决。空间域卷积的论文也比较多:DCNN(扩散卷积)、GraphSage、GAT(基于self-attention)、LGCN(邻居采样+top-k selection+ 1DCNN)等等,其实后面讲的模型都是空间域卷积,有比较有代表性的模型即GraphSAGE:
 图 5
图 5
该模型指出,以前的模型的目标是为每个不同的节点学习到一个唯一的Embedding,这导致模型的可扩展性很差。本论文[7]提出GraphSAGE将目标定于学习聚合器,聚合器的任务在于完成邻居节点的信息聚合,因此GraphSAGE不会因为新节点的加入而造成模型无法工作。除此之外,GraphSAGE支持分批训练。
如图5,该模型的工作步骤可以分为:
分批采样若干源节点,对于其中一个中心节点来说,首先对其一阶邻居采样固定数目个节点,若感受野为2,则在对中心节点的每个一阶邻居的邻居节点进行固定数目的采样,采样数目为超参数。一般感受野的大小K=2.
采样结束后,对节点的邻居节点进行聚合,其聚合方式应该具有排列不变性,作者提供了三种:(i)mean,(ii)max, (iii)lstm,其中mean的聚合方式让模型近似等价于论文[6],lstm不具有排列不变性。
中心节点的K阶邻域聚合完毕后,通过concat或sum的形式两者进行融合,获得最后的embdding,然后用于半监督学习或者无监督学习。
其分批算法流程可以表示为:
 图 6
图 6
具体的算法细节,大家可以参考源码,这篇论文十分适合落地。
值得一提,这篇论文也存在着一定的缺陷,后面会提到。
下面在分别讲一下几个重要的研究方向,分类可能不太对,大家凑活着看。
3. Analysis
 图 7
图 7
论文[8]提出了一种描述GNN的通用框架即信息传递机制。其核心思想很简单,通过中心节点、其一个邻接节点和它们之间的边信息生成一个信息M,然后将中心节点能生成的所有信息加和得到m,然后将该信息传递给中心节点做一个融合得到新的Embedding。若是做图分类任务,则再加入一个Readout层来做一个全局的池化。其实这种思想在论文[9]中也有提高过。
作者认为大家的模型都应该按照他的框架来,红红火火恍恍惚惚红红火火\(^o^)/~。
在通用框架方面,还有非常多的代表性论文,Relational Inductive Biases, Deep Learning, and Graph Networks.arxiv 2018.paper,这篇论文中也提出了非常多的框架。
 图 8
图 8
论文[10]探讨了什么样的模型能够有更强大的表达能力。早在GraphSAGE中,作者就提出了空间域卷积的操作与Weisfeiler-Lehman test十分相似, WL test的流程如下:
聚合节点的节点与他们邻居节点的标签。
对聚合结束后的新标签进行hash操作。
迭代1、2几次,观察标签的分布来判断图是否同构。
如图8中间的图所示,GNN的聚合和WL test都能得到一个类似树的结构,作者认为拥有不同子树的根节点应该拥有不同的Embedding。
这就引出了作者的一个理论:
 图 9
图 9
简单一点说,聚合函数f、 、readout的函数映射是单射的。
作者据此,设计了一种能够发挥最大表达能力的模型,即图8最下方的模型。该模型聚合函数使用了加和(作者在论文中对比了mean、max和sum的优劣),使用了MLP,readout使用了跨层级的加和操作。
 图 10
图 10
论文[11] 探讨了强大的图神经网络的必要性问题,作者在文中去除了那些复杂的聚合操作,之加入一些线性变化和激活函数,在readout层使用MLP来增强网络。
网络的输入数据有进行更改,其数据位节点度、节点信息,节点K接邻居信息的concat结果,可以认为作者仅仅通过在输入数据中加入度信息和邻居信息,而用线性变化和激活函数代替邻域节点聚合操作仍能在图分类任务上取得很好地效果。(后面有篇论文特别强调了度信息的重要性)。从这点看来,图神经网络应该是什么样的还处于混沌状态。我们怎么才能更加有效地、更加高效率的获取数据中的结构信息呢。
4 Efficiency
图神经网络领域还有一个关于模型效率的方向。
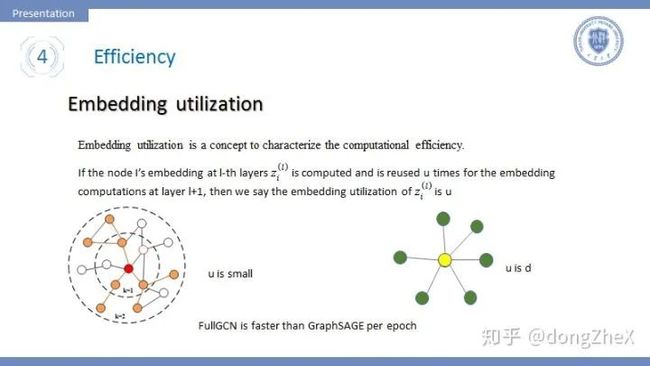 图 11
图 11
首先引入一个概念Embedding utilization,该概念最早提出在论文[12]中。如果一个节点在l层中被采样计算,并且在l+1层重复利用u次,我们说节点利用率为u。这个指标可以很好地衡量模型的时间复杂度,embedding utilization跟采样图中边数量成正比。
这里说一个事实,虽然GraphSAGE采用了分批训练极大地提升了模型的的收敛速度,但是其每个epoch的时间却比FullGCN[6]要慢很多,这用Embedding utilization可以很好地解释。
可以很容易的想到,在GraphSAGE中的u是很小的,这一层采样的节点在下一层也被采样的几率是不大的。而对于FullGCN这种全采样的方法,u是节点度的平均值,很明显要大于GraphSAGE,所以GraphSAGE的per-epoch time要更长。
接下来介绍几种重要的采样方式:
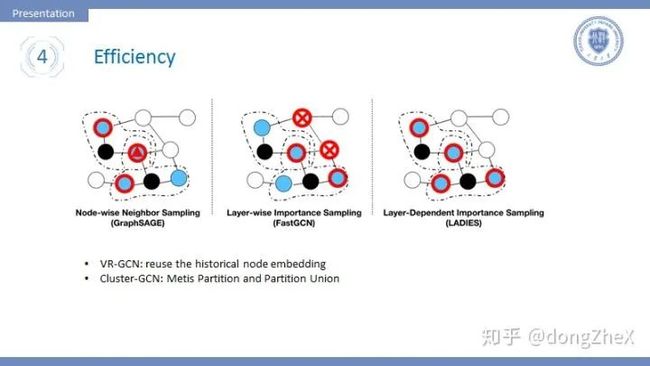 图 12
图 12
Node-wise:其代表就是GraphSAGE,每次采样中心节点固定数目的邻居节点,这种方法面临的问题是,当网络层数变深时,模型的复杂程度指数增加。
Layer-wise:该方法进行层间独立采样,在每一层中都单独采样固定数目的节点,这样就不会有指数级的复杂度,并且采样遵循重要性采样方法(具体见论文[13]、[14])。这种方法面临的问题是,节点间的关系可能很稀疏,导致模型的效果下降。
Layer-wise x Node-wise: 论文[15]提出一种方法,在层间独立采样的基础上,在第一层采样固定数目节点,然后下一层的采样在第一层所有节点的邻居节点中采样固定数目节点,这样可以同时减少复杂度、减弱稀疏。
基于图划分:论文[15]提出了一种基于图划分的方式,首先使用METIS划分算法对图进行划分,划分结果趋向于拥有更多的边,然后在这个图划分中完成图卷积操作可以有效提升节点利用率。有一个问题,划分之间的关系很可能损失掉,这会导致模型性能下降,作者采用将多个划分合并的方法来减弱这种趋势。
这个研究领域的成果其实并不是具体的模型,而是一种训练方法,这是需要注意的。
5.Pooling
对应于传统深度学习中的pooling,GNN中也有池化操作,这方面我看的论文不是很多,简单介绍一下。Pooling常用于图分类任务中。
 图 13
图 13
Pooling常用于readout中进行全局池化,最基本的方法有Max-pooling、SUM-pooling、mean-pooling等。
论文[16]首次将attention加入到pooling操作中(在这之前有GAT网络用于图卷积,大家有兴趣可以查看相关论文)。该方法的步骤如下:
使用FullGCN进行操作得到每个节点的一个Embedding。
根据Embedding计算top-k节点,然后删除剩余节点。
将top-k进行Max-pooling、Mean-pooling进行池化,在用MLP进行映射进而完成图分类任务。
作者在论文中给出了两种模型搭建方式,可分别应用于大图数据和小图数据中,具体大家可以参考论文。
这里说一下attention的问题,attention最近在GNN领域的应用非常多,比较有代表性的就是GAT这个模型,具体的大家可以看论文。这里我想说一下我理解的attention在GNN中作用:一是帮助结构特征的提取,帮助我们得知哪个邻居更加重要,需要更大的权重。二是帮助构造节点序列,在CNN中卷积核中心节点的周围节点都因为相对位置而获得顺序,但是图节点的邻居并没有顺序,这时候通过attention机制可以帮助我们搞定节点顺序选择问题。attention我觉得可以作为一个小trick用到各种模型中来加强模型效果。
有研究者发现,目前的pooling方法没有类似于传统pool的层级结构,论文[19]就此提出了DiffPool模型。
 图 14
图 14
模型的思想是这样的,在模型的前向传播过程中,加入一个矩阵S,S的作用是将当前层的节点进行划分,划分后节点的数目减少,在网络的最后划分数目变为1。其计算过程如图14左侧所示,更加具体的操作细节,可以参考论文原文。
这个S如何获得呢,答案是通过学习获得。模型被分为两部分,一部分学习节点的embedding,一部分用于学习矩阵S(其中用到了top-k的思想),其计算模型如图14中间所示。
作者在训练过程中,发现模型很难收敛,遂加入一个新的损失项,该损失基于假设:邻居节点应该尽可能的被分在同一个划分中。
6.About Experiment
看这方面论文很惊悚,让我感觉以前的实验真的白做了。
 图 15
图 15
论文[18]做了这样一个工作,他在一个统一的实验设置下,对当前重要的模型进行测试。
论文指出现今的模型存在一个问题,他们的实验设置非常不同,不同的实验导致会导致模型效果天差地别,并且缺少可再现性。。最近自己在做实验的时候也深有体会,无论如何也无法复现一些论文中的效果,增加训练集节点数目会让效果天差地别。
作者将模型评价分为两个阶段:(i)model selection (ii) model assessment。前者为超参数的选择阶段,后者为模型结果测试阶段。一个合格的评价流程可以提高模型的可再现性。
就此作者提出了一套基于交叉验证的评测流程,如图15所示。
除此之外,我还得知了并非所有的数据都有节点特征,像如reddit这样的社交网络数据是缺少节点特征的,论文采用的方法是将节点特征设置为相同值或者度的独热编码。
论文在完成测试后,得到两个重要结论:
一些没有适用结构特征提取的方法在某些情境下,效果优于GNN,所以这告诉我们当前的GNN模型没有充分提取结构信息。
节点的度是一个非常重要的特征,能够显著提升模型效果,这也印证了之前的GFN模型。
现在在图神经网络领域还缺少一个像ImageNet这样的评测平台,不可否认的是ImageNet对于计算机视觉的发展推动十分大。所以我们需要这样一个平台。
 图 16
图 16
论文[19]做了一个benchmark。
该论文指出当前工作常用的引文网络数据集存在很大的问题,它的数据规模太小了,这对于开发更加复杂的图神经网络模型是十分不利的。一些好的模型会在这些数据集上趋向于过拟合而不是提升泛化能力。
所以作者在计算机视觉、生物信息、社交网络等领域建立了多个中等规模的数据集,并使用一致的评测流程来保证公平,希望这个benchmark可以促进图神经网络的发展。
7.GNN领域中的一些问题:
训练方式问题(sampling):目的是寻找一种训练方式,使得收敛速度加快、time per epoch时间降低,并且不明显损耗效果。值得一提VR-GCN在重要性采样这一方面已经做到了方差为0,很不错了。
Deep network : GNN现在一般的层数为2-3层,研究者发现加深网络会导致模型的效果变差。我理解的有以下几种解释方法:(1)拉普拉斯矩阵的幂运算在指数很大时, 变化很小。(2)GCN它基于假设:让相邻的节点尽可能的处于同一类,如果加深层数会导致距离比较远(不属于同一类)的节点成为同类,这明显会损耗GNN效果。(3)当GNN的层数加深,会聚集更多节点的noise information。(4)当GNN层数加深时,中心节点的节点特征会慢慢地被丢弃,所以有工作通过加多个自旋的方式来加深层数。(5)统计学常识:参数越多,需要的数据越多,然而没有大型图数据集。解决加深GNN层数的问题主要使用skip connection的方法,如残差网络,hightway network,Dilated 等方法。
异质图:异质图中的节点和边拥有不同的类型,异质图问题一般很复杂,现在也有很多相关的工作,其中一个重要思想是先想办法将节点和边分类,然后进行类内的信息聚合,然后在进行类间的节点聚合。
有向图:前面提到的很多GNN模型只面向无向图,要想处理有向图,就必须考虑child和father这一项信息。
动态图:图中的节点信息、节点存在与否动态变化,这要求模型泛化能力极强并且拥有很好的灵活性。
有信息的边:遇到带信息的边,需要考虑边带有的信息。现在有这么几个方法:(i)将边变为一个节点和两条边,这样就去掉了信息边。(ii)不同的边拥有不同的参数矩阵(需要考虑参数数量问题)。
其github的地址:
GitHub - graphdeeplearning/benchmarking-gnns: Repository for benchmarking graph neural networks github.com
其配置流程可以参考我的一篇文章:
dongZheX:Win10安装配置Benchmark for GNN zhuanlan.zhihu.com
给大家推荐一个库pyG,大家可以用这个库来实现baseline模型,能够很好的提升效率。
https://github.com/rusty1s/pytorch_geometric github.com
给大家推荐一个找论文的好地方:
GitHub - thunlp/GNNPapers: Must-read papers on graph neural networks (GNN) github.com
ppt的链接:
链接:pan.baidu.com/s/1zo0cwk
提取码:eddm
我感觉我写的脉络性不是特别的强,如果想系统学习一下可以参考一些综述,推荐几篇:
A Comprehensive Survey on Graph Neural Networks.arxiv 2019.paper
Relational Inductive Biases, Deep Learning, and Graph Networks.arxiv 2018.paper
Geometric Deep Learning: Going beyond Euclidean data.IEEE SPM 2017.paper
写写代码可以先看这个github,自己写写试试:
https://github.com/FighterLYL/GraphNeuralNetwork github.com
大概就说这么多啦,最新的论文还没看,心情不好,忙着搞毕设呢,以后再更。这是初稿,欢迎大家指出不准确的地方。
参考论文:
[1] Wu Z, Pan S, Chen F, et al. A comprehensive survey on graph neural networks[J]. arXiv preprint arXiv:1901.00596, 2019.
[2] Monti, Federico, Boscaini, Davide, Masci, Jonathan,等. Geometric deep learning on graphs and manifolds using mixture model CNNs[J].
[3] Niepert M, Ahmed M, Kutzkov K. Learning convolutional neural networks for graphs[C]//International conference on machine learning. 2016: 2014-2023.
[4] Bruna, Joan, Zaremba, Wojciech, Szlam, Arthur,等. Spectral Networks and Locally Connected Networks on Graphs[J]. Computer Science, 2013.
[5] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Advances in neural information processing systems. 2016: 3844-3852.
[6] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
[7] Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs[C]//Advances in Neural Information Processing Systems. 2017: 1024-1034.
[8] Gilmer J , Schoenholz S S , Riley P F , et al. Neural Message Passing for Quantum Chemistry[J]. 2017.
[9] Relational Inductive Biases, Deep Learning, and Graph Networks. Battaglia, Peter W and Hamrick, Jessica B and Bapst, Victor and Sanchez-Gonzalez, Andrea and Raposo, David and Santoro, Adam and Faulkner, Ryan and others. 2018. Paper
[10] Xu K, Hu W, Leskovec J, et al. How powerful are graph neural networks?[J]. arXiv preprint arXiv:1810.00826, 2018.
[11] Chen, Ting, Bian, Song, Sun, Yizhou. Are Powerful Graph Neural Nets Necessary? A Disp on Graph Classification[J].
[12] Chiang W L, Liu X, Si S, et al. Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks[J]. arXiv preprint arXiv:1905.07953, 2019.
[13] Chen J, Ma T, Xiao C. Fastgcn: fast learning with graph convolutional networks via importance sampling[J]. arXiv preprint arXiv:1801.10247, 2018.
[14] Stochastic training of graph convolutional networks with variance reduction[J]. arXiv preprint arXiv:1710.10568, 2017
[15] Layer-Dependent Importance Sampling for Training Deep and Large Graph Convolutional Networks[C]//Advances in Neural Information Processing Systems. 2019: 11247-11256.
[16] Lee, Junhyun, Inyeop Lee, and Jaewoo Kang. "Self-attention graph pooling."arXiv preprint arXiv:1904.08082(2019).
[17] Ying Z, You J, Morris C, et al. Hierarchical graph representation learning with differentiable pooling[C]//Advances in neural information processing systems. 2018: 4800-4810.
[18] Errica F, Podda M, Bacciu D, et al. A fair comparison of graph neural networks for graph classification[J]. arXiv preprint arXiv:1912.09893, 2019.
[19] Dwivedi V P, Joshi C K, Laurent T, et al. Benchmarking Graph Neural Networks[J]. arXiv preprint arXiv:2003.00982, 2020.
![]()