图像的同态滤波原理及实现
图像的同态滤波原理及实现
同态滤波(Homomorphic filter)是信号与图像处理中的一种常用技术,它采用了一种线性滤波在不同域中的非线性映射。这一技术是上世纪60年代由麻省理工学院(MIT)的Thomas Stockham,Alan V. Oppenheim和 Ronald W. Schafer 等几位学者提出。
如果您对原理部分不感兴趣,可直接跳至双虚线以下的关键代码实现部分。
首先,介绍两个概念。
同态系统:是将非线性问题,转化为线性问题处理。即对非线性(乘性)混杂信号,通过某种数学运算(如对数变换),变成加性模型,而后采用线性滤波方法进行处理。
同态滤波:是把频率滤波和空域灰度变换结合起来的一种图像处理方法,它根据图像的照度/反射率模型作为频域处理的基础,利用压缩亮度范围和增强对比度来改善图像的质量。
下面介绍关于同态滤波的基本原理。
一幅图像可看成由两部分组成,即
![]()
其中,fi代表随空间位置不同的光强(Illumination)分量,其特点是缓慢变化,集中在图像的低频部分。fr代表景物反射到人眼的反射(Reflectance)分量。其特点包含了景物各种信息,高频成分丰富。
同态滤波过程,分为以下5个基本步骤:
① 原图做对数变换,得到如下两个加性分量,即
![]()
② 对数图像做傅里叶变换,得到其对应的频域表示为:
![]()
③ 设计一个频域滤波器H(u,v),进行对数图像的频域滤波。
④ 傅里叶反变换,返回空域对数图像。
⑤ 取指数,得空域滤波结果。
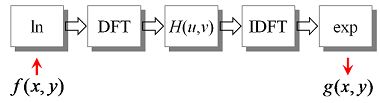
综上,同态滤波的基本步骤如图1所示。
图1 同态滤波的基本步骤
可以看出,同态滤波的关键在于滤波器H的设计。对于一幅光照不均匀的图像,同态滤波可同时实现亮度调整和对比度提升,从而改善图像质量。为了压制低频的亮度分量,增强高频的反射分量,滤波器H应是一个高通滤波器,但又不能完全cut off 低频分量,仅作适当压制。
因此,同态滤波器一般采用如下形式,即
![]()
其中,gL< 1, gH >1,控制滤波器幅度的范围。Hhp通常为高通滤波器,如高斯(Gaussian)高通滤波器、巴特沃兹(Butterworth)高通滤波器、Laplacian滤波器等。
如果Hhp采用Gaussian高通滤波器,则有:
![]()
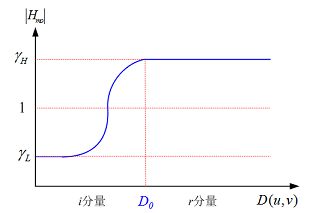
其中,c为一个常数,控制滤波器的形态,即从低频到高频过渡段的陡度(斜率),其值越大,斜坡带越陡峭,见图2。
图2 同态滤波器幅频曲线
================================================================================
同态滤波的原理就这么简单,不过写代码实现起来,具体问题就来了。你不妨百度一下,网上一些论坛里,贴有大量可参考的代码,让您看了像雾像雨又像云,很可能会误导你。那么,只有吃透了原理,或自己动手测试一下,方能做出正确判断。
实现对一幅输入图像同态滤波的关键(MATLAB)代码如下:
① 输入图像取对数,一般取自然对数,即
f = log(1+I); % log transformation
这里图像I做对数变换前,需要转化为double型。针对灰度范围[0~255]的图像数据,log(I+1)是为了满足真数大于0,以防计算无意义。特别提醒,如果是归一化图像数据,则建议log(I+0.01)。
② 对f做FFT,此步涉及后续的频域滤波。因此,FFT前数据f一般需零填充至本身的2倍尺寸。
Fp = fft2(f,P,Q); % FFT with zeros padding
这里,P = 2M, Q = 2N, M, N为数据f的阵列大小。
③ 滤波器H设计,滤波器尺寸同样应为P、Q。
[v, u] = meshgrid(1:Q, 1:P); % [y, x] = size(I),y为行数,x为列数。与习惯顺序[x, y]有点反,易混淆!
u = u - floor(P/2); % u方向 centralization
v = v - floor(Q/2); % v方向 centralization
D = u.^2 + v.^2; % compute the distances
H = 1-exp(-c*(D./D0^2)); % gaussian high-pass filter
H = (rH - rL)*H + rL; % homomorphic filter
这里,D0为gaussian滤波器的截止频域。因产生的为中心化滤波器,下一步滤波f的傅里叶变换也需要中心化处理;否则,H反中心化。
④ 频域滤波。
H = ifftshift(H); % H反中心化,因Fp未中心化!
Gp = Fp.*H; % filtering in frequency domain
⑤ 傅里叶反变换,返回空域的对数图像。
gp = real(ifft2(Gp)); % IFFT取实部。网上有些代码直接取abs,计算误差会引起虚部不为零。No!
g = gp(1:M,1:N); % 截取有效数据
⑥ 取指数,得空域滤波结果。
g = exp(g)-1; % 先前取对数时,为log(1+I)。 有代码先在频域做exp(Gp),再反变换。No!
⑦ 显示g时,适当做数据的映射处理,以适合人眼观察。
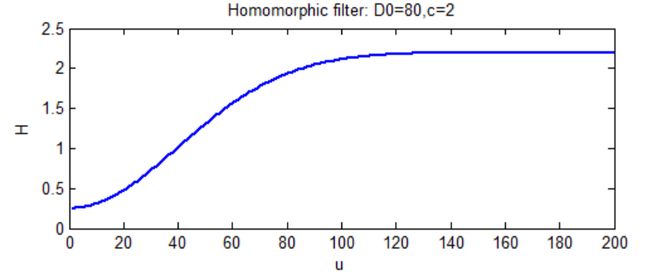
以下为利用以上原理和关键代码实现的两个场景下的同态滤波实验。H参数的设置为:D0=80, rL =0.25, rH=2.2, c=2.0。其幅频曲线如图3所示。
图3 设置参数下的同态滤波器幅频图
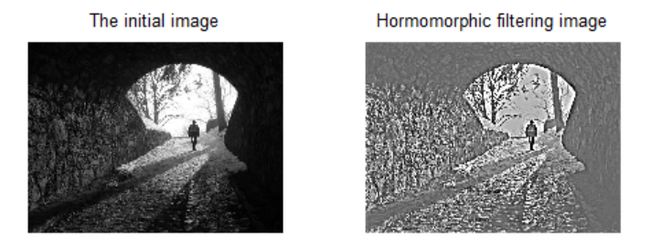
图4 同态滤波结果,PET扫描图(上),隧洞口场景(下)
注:以上代码实现中,未考虑边界问题。关于边界处理问题,请参考前述博文:如何保持空域与频域滤波结果的一致性(续)。
读者如需完整代码,可直接联系本人。
推荐参考:
[1]https://en.wikipedia.org/wiki/Homomorphic_filtering
[2]http://blogs.mathworks.com/steve/2013/06/25/homomorphic-filtering-part-1/
[3]http://blogs.mathworks.com/steve/2013/07/10/homomorphic-filtering-part-2/
[4]http://bbs.sjtu.edu.cn/bbstcon?board=DSP&reid=1316225259
《教学后记》序列博文:
[1] 频域Laplacian图像锐化原理与实现
[2] 如何保持空域与频域滤波结果的一致性(续)
[3] 傅里叶变换的波形分辨率与频率分辨率
[4] 如何保持空域与频域滤波结果的一致性