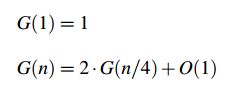目录
- 1.数据结构定义
1.1 定义
1.2 一维k-d树(1-d树——二叉搜索树)
1.3 二维k-d树(2-d树)
1.4 k-d树的结构性质 - 2.应用
- 3.数据结构以及操作
3.1 Weiss《数据结构与算法分析》中简单的定义
3.2 UFL(佛罗里达大学)课程给出的定义
3.3 一个经典的定义
1.数据结构定义
1.1 定义
k-d树(k-dimensional tree),是一棵二叉树,树中存储的是一些k维数据。在一个k维数据集合上构建一棵k-d树代表了对k维数据集合构成的k维空间的一个划分,即树中的每个结点就对应了一个k维的超矩形区域。
1.2 一维k-d树(1-d树——二叉搜索树)
对于一维的情况,所有的点都在数轴上面,此时 k-d树 其实就是二叉搜索树。
二叉搜索树(Binary Search Tree,BST),是具有如下性质的二叉树:
- 若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树;
例如,下图是一棵二叉搜索树,其满足 BST 的性质。
1.3 二维k-d树(2-d树)
对于每一层,可以指定一个划分维度(轴垂直分区面axis-aligned splitting planes),最简单的就是按照关键字轮流划分(例如:奇数层按照x轴划分,也即第一个关键字;偶数层按照y轴划分,也即第二个关键字)。
1.4 k-d树的结构性质
一棵随机构造的2-d树与一棵随机二叉搜索树具有相同的结构性质:高度平均为O(lgN),但最坏情形则是O(N)。
不像二叉搜索树有精巧的O(lgN)最坏情况的变种在,没有已知的方案能够保证一棵平衡的2-d树。问题在于,这样一种方案很可能基于树的旋转,而树旋转在2-d树中是行不通的。
最好的办法是通过重新构造子树来定期对树进行平衡。
2.应用
多维键值搜索(例:范围搜寻及最邻近搜索)。
例如:一广告公司拥有一个数据库并需要为某些客户生成邮寄标签。典型的要求可能是需要散发邮件给那些年龄在34-49之间且年收入在100000美元到150000美元之间的人们。这个个问题叫做二维范围查询。
3.数据结构以及操作
3.1 Weiss《数据结构与算法分析》中简单的定义
1)性质
在奇数层上的分支按照第一个关键字进行,而在偶数层上的分支按照第二个关键字进行。
2)插入
代码中通过!level不断取反,交替取值0、1来在两个维度进行交替判断
3)查询
- 要求精确匹配
- 部分匹配查询——基于两个关键字中一个关键的匹配
上面两种都是(正交)范围查询的特例。
正交范围查询给出其第一个关键字在一个特殊的值集合之间且第二关键字在另一个特殊的的值集合之间的所有项。
3.2 UFL(佛罗里达大学)课程给出的定义
COMPUTATIONAL GEOMETRY
1)性质
分割跟Weiss的定义类似,偶数层深度用垂直的线进行分割,奇数层用水平线进行分割。
2)建k-d树
不断使用中位数进行分割,达到平衡。
3)查询
4)查询时间分析
-
针对区域v的查询,分为三类点
-
灰结点分析
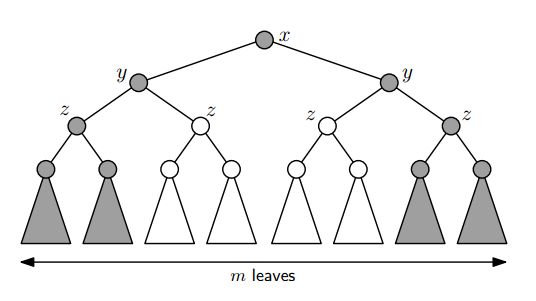
这个可以得到G(n) = √n
如下是定理:
高维情况:
3.3 一个经典的定义
k-d tree算法
1)应用背景
- SIFT算法中做特征点匹配的时候就会利用到k-d树。而特征点匹配实际上就是一个通过距离函数在高维矢量之间进行相似性检索的问题。针对如何快速而准确地找到查询点的近邻,现在提出了很多高维空间索引结构和近似查询的算法,k-d树就是其中一种。
- 索引结构中相似性查询有两种基本的方式:一种是范围查询(range searches),另一种是K近邻查询(K-neighbor searches)。范围查询就是给定查询点和查询距离的阈值,从数据集中找出所有与查询点距离小于阈值的数据;K近邻查询是给定查询点及正整数K,从数据集中找到距离查询点最近的K个数据,当K=1时,就是最近邻查询(nearest neighbor searches)。
- 征匹配算子大致可以分为两类。一类是线性扫描法,即将数据集中的点与查询点逐一进行距离比较,也就是穷举,缺点很明显,就是没有利用数据集本身蕴含的任何结构信息,搜索效率较低,第二类是建立数据索引,然后再进行快速匹配。因为实际数据一般都会呈现出簇状的聚类形态,通过设计有效的索引结构可以大大加快检索的速度。索引树属于第二类,其基本思想就是对搜索空间进行层次划分。根据划分的空间是否有混叠可以分为Clipping和Overlapping两种。前者划分空间没有重叠,其代表就是k-d树;后者划分空间相互有交叠,其代表为R树。(这里只介绍k-d树)
2)数据结构
3)k-d树的构建
构建实例如下:
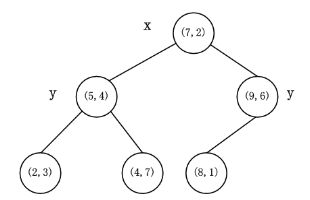
假设有6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间内。
由于此例简单,数据维度只有2维,所以可以简单地给x,y两个方向轴编号为0,1,也即split={0,1}。
- 1.确定split域的首先该取的值。分别计算x,y方向上数据的方差得知x方向上的方差最大,所以split域值首先取0,也就是x轴方向;
- 2.确定Node-data的域值。根据x轴方向的值2,5,9,4,8,7排序选出中值为7,所以Node-data = (7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于split = 0(x轴)的直线x = 7;
-
3.确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分,如图2所示。x < = 7的部分为左子空间,包含3个节点{(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点{(9,6),(8,1)}。
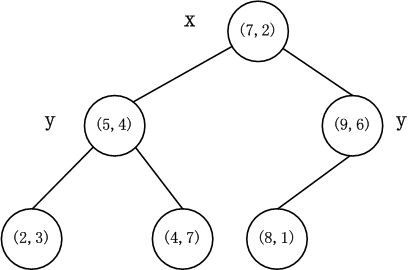
k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点(5,4)和(9,6)(也就是左右子空间的'根'节点),同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点,如图2所示。最后生成的k-d树如图3所示。
4)k-d树的最邻近查找算法
4-1)查询点(2.1, 3.1)
通过二叉搜索,顺着搜索路径很快就能找到最邻近的近似点,也就是叶子节点(2,3)。而找到的叶子节点并不一定就是最邻近的,最邻近肯定距离查询点更近,应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻,还需要进行'回溯'操作:算法沿搜索路径反向查找是否有距离查询点更近的数据点。此例中先从(7,2)点开始进行二叉查找,然后到达(5,4),最后到达(2,3),此时搜索路径中的节点为<(7,2),(5,4),(2,3)>,首先以(2,3)作为当前最近邻点,计算其到查询点(2.1,3.1)的距离为0.1414,然后回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以(2.1,3.1)为圆心,以0.1414为半径画圆,如图4所示。发现该圆并不和超平面y = 4交割,因此不用进入(5,4)节点右子空间中去搜索。
再回溯到(7,2),以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面交割,因此不用进入(7,2)右子空间进行查找。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414。
4-2)查询点(2, 4.5)
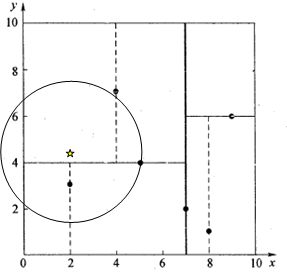
同样先进行二叉查找,先从(7,2)查找到(5,4)节点,在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),形成搜索路径<(7,2),(5,4),(4,7)>,取(4,7)为当前最近邻点,计算其与目标查找点的距离为3.202。然后回溯到(5,4),计算其与查找点之间的距离为3.041。以(2,4.5)为圆心,以3.041为半径作圆,如图5所示。可见该圆和y = 4超平面交割,所以需要进入(5,4)左子空间进行查找。此时需将(2,3)节点加入搜索路径中得<(7,2),(2,3)>。回溯至(2,3)叶子节点,(2,3)距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5。回溯至(7,2),以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如图6所示。至此,搜索路径回溯完。返回最近邻点(2,3),最近距离1.5。