视觉SLAM中的对极约束、三角测量、PnP、ICP问题

  这篇博客是在学习高翔《视觉SLAM十四讲》过程中对计算机视觉的多视图几何相关知识点做的总结，个人觉得这部分内容比较难，有理解不对的地方请指正！

〇、ORB特征点

  对于特征点法的SLAM来说，ORB(Oriented FAST and Rotated BRIEF)特征应该是目前最合适的特征点了。ORB与SIFT、SURF之间的性能对比如下：

• 计算速度：ORB >> SURF >> SIFT（各差一个量级）
• 旋转鲁棒性：SURF > ORB ~ SIFT
• 模糊鲁棒性：SURF > ORB ~ SIFT
• 尺度变换鲁棒性：SURF > SIFT > ORB（ORB算法在尺度方面效果较差）

  特征点由关键点和描述子两部分组成，对于ORB特征点来说，它使用的是FAST关键点+BRIEF描述子。

  FAST是一种角点，主要检测局部像素灰度变化明显的地方，以速度快著称。但FAST角点本身并不具有尺度和方向信息，针对这一问题，ORB算法通过构建图像金字塔，并在金字塔的每一层上检测角点来实现FAST的尺度不变性；用灰度质心法来实现FAST的旋转不变性。在ORB中，将这种可以描述角点尺度与旋转特性的FAST称为Oriented FAST。

  BRIEF是一种二进制描述子，为关键点添加描述子的作用是为了实现图像之间的特征匹配。BRIEF使用了随机选点的比较，速度非常快，而且由于使用了二进制表达，存储起来也十分方便。但原始的BRIEF描述子不具有旋转不变性，图像发生旋转时容易丢失，针对这一问题，ORB算法利用在FAST角点提取阶段计算出的关键点方向信息，使BRIEF具有了较好的旋转不变性。

  有了ORB特征点，我们需要用它来做图像间的特征匹配。所谓特征匹配，就是比较特征点的相似度，这个相似度通过它们的描述子来计算。对于BRIEF这种二进制的描述子，通常使用汉明距离（Hamming distance）来度量两个特征点之间的相似程度。汉明距离是指两个长度相等的字符串之间不同数据位的个数，例如：两个8位的二进制串00110100与10110100，它们之间只有第一个数据位不同，所以它们的汉明距离为1。在ORB的特征匹配中，汉明距离越小，特征点的相似度越高，在某种程度上，我们可以认为两个特征点在两帧图像中为同一个点，即完成了特征匹配。

  特征匹配在视觉SLAM中真的是至关重要的一步，设想一下，假如每一帧图像都能实现100%的正确匹配，那我们就不再需要各种令人头疼的滤波、优化、回环检测等等，这将是一个多么美好的画面啊啊啊。。。但，现实告诉你，绝大部分的图像之间是不可能做到100%正确匹配的，所以说，SLAM的主要工作在后端，就是如何利用不准确的数据估计得到准确的结果。

  当然，下面总结的在视觉SLAM中经常用到的，非常重要的，Multiple View Geometry in Computer Vision中的，比较难以理解又容易混淆的几个算法，都是在理想的特征匹配结果之上推导出来的。

一、对极几何

  对极几何（Epipolar geometry）又叫对极约束，是根据图像二维平面信息来估计单目相机帧间运动或双目相机相对位姿关系的一种算法。直观来讲，当相机在两个不同视角对同一物体进行拍摄时，物体在两幅图像中的成像肯定会有不同，那么，根据这两幅不同的图像，我们如何判断出相机的位姿发生了怎样的变化，这正是对极几何要解决的问题。

  需要明确的是，在对极几何中，我们的已知条件仅仅是每幅图像中特征点的像素坐标，当然，计算对极约束的前提是我们必须知道两幅图像中特征点之间准确的匹配关系。

图1 对极几何示意图

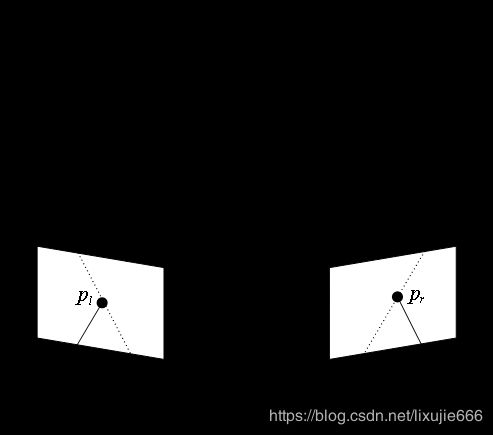
  如图1所示，以其中一对匹配点为例。$P$为空间中的一点（坐标未知），其在左边图像中的投影为$p_l=[u_l,v_l,1{]}^{\text{T}}$，在右边图像中的投影为$p_r=[u_r,v_r,1{]}^{\text{T}}$，当我们以相机坐标系$O_L$为参考坐标系时，有：
$$\{\begin{array}{l}{s}_l{p}_l=KP\\ s_r{p}_r=K(RP+t)\end{array}⟹\{\begin{array}{l}{s}_l{K}^{-1}{p}_l=P\\ s_r{K}^{-1}{p}_r=RP+t\end{array}\text{\hspace{1em}(1)}$$

其中$s_l$、$s_r$分别为点$P$在相机坐标系$O_L$、$O_R$中的$z$坐标值（即深度），$K$为$3\times 3$的相机内参矩阵，$R$、$t$即为$O_L$与$O_R$之间的相对位姿关系。取$x_l=K^{-1}{p}_l,x_r=K^{-1}{p}_r$，则有：
$$\{\begin{array}{l}{s}_l{x}_l=P\\ s_r{x}_r=RP+t\end{array}⟹s_r{x}_r=R(s_l{x}_l)+t⟹s_r{x}_r=s_{l}R{x}_l+t\text{\hspace{1em}(2)}$$

  上式两边同时左乘$t$的反对称矩阵$t^{\wedge }$，相当于两侧同时与$t$做外积（$t$与自身的外积$t^{\wedge }t=0$）：
$$s_r{t}^{\wedge }{x}_r=s_l{t}^{\wedge }R{x}_l\text{\hspace{1em}(3)}$$

  然后，两侧同时左乘$x_r^{\text{T}}$：
$$s_r{x}_r^{\text{T}}{t}^{\wedge }{x}_r=s_l{x}_r^{\text{T}}{t}^{\wedge }R{x}_l\text{\hspace{1em}(4)}$$

  上式左侧中，$t$与$x_r$的外积$t^{\wedge }{x}_r$是一个与$t$和$x_r$都垂直的向量，所以，再将$x_r^{\text{T}}$与$t^{\wedge }{x}_r$做内积，其结果必为$0$，从而有：
$$s_l{x}_r^{\text{T}}{t}^{\wedge }R{x}_l=0⟹s_l(K^{-1}{p}_r{)}^{\text{T}}{t}^{\wedge }R(K^{-1}{p}_l)=0⟹p_r^{\text{T}}{K}^{\text{-T}}{t}^{\wedge }R{K}^{-1}{p}_l=0\text{\hspace{1em}(5)}$$

  (5)式以非常简洁的形式描述了两幅图像中匹配点对$p_l$和$p_r$之间存在的数学关系，这种关系就叫对极约束。另外，我们称$E=t^{\wedge }R$为本质矩阵（Essential Matrix），称$F=K^{\text{-T}}{t}^{\wedge }R{K}^{-1}=K^{\text{-T}}E{K}^{-1}$为基础矩阵（Fundamental Matrix），于是(5)式可以进一步简化为：
$$x_r^{\text{T}}E{x}_l=p_r^{\text{T}}F{p}_l=0\text{\hspace{1em}(6)}$$

  OK，现在我们需要重新明确一下对极几何的工作：对极几何是要利用已知的$n$对如上述$p_l$、$p_r$这样的匹配点（二维像素坐标），来计算相机的运动$R$、$t$，即求解本质矩阵$E$或基础矩阵$F$。具体求解过程可参看《视觉SLAM十四讲》P143-148。

  对极几何存在的问题：根据对极约束求解得到的相机旋转运动$R$是准确的，平移运动$t$是不具备真实尺度的。

二、三角测量

  三角测量（Triangulation）又叫三角化，是根据前后两帧图像中匹配到的特征点像素坐标以及两帧之间的相机运动$R$、$t$，计算特征点三维空间坐标的一种算法。直观来讲，当有两个相对位置已知的相机同时拍摄到同一物体时，如何根据两幅图像中的信息估计出物体的实际位姿，即通过三角化获得二维图像上对应点的三维结构，这正是三角测量要解决的问题。

图2 三角测量示意图

  如图2所示为三角测量基本原理的示意图，该图与图1非常相似，但应该注意其中的区别：此时我们已经知道了$O_L$与$O_R$的关系，$p_l$、$p_r$也是已知的，要求的是点$P$的三维空间坐标。由(1)式我们知道，要求点$P$的三维坐标，需要先求深度$s$；由(2)式我们有：
$$s_r{x}_r=s_{l}R{x}_l+t\text{\hspace{1em}(7)}$$

对上式两侧左乘一个$x_r$的反对称矩阵$x_r^{\wedge }$，得：
$$s_r{x}_r^{\wedge }{x}_r=s_l{x}_r^{\wedge }R{x}_l+x_r^{\wedge }t⟹s_l{x}_r^{\wedge }R{x}_l+x_r^{\wedge }t=0\text{\hspace{1em}(8)}$$

  (8)式是一个超定方程组（Overdetermined system），通常只能求得它的最小二乘解。当我们求出$s_l$后，根据(7)式就很容易求出$s_r$，最后由(1)式，我们有：
$$\{\begin{array}{ll}{s}_l{K}^{-1}{p}_l=P_{O_L}，& \text{POL表示点P在相机坐标系OL下的三维坐标 }\\ s_r{K}^{-1}{p}_r=P_{O_R}，& \text{POR表示点P在相机坐标系OR下的三维坐标 }\end{array}\text{\hspace{1em}(9)}$$

  上式中$P_{O_L}$与$P_{O_R}$之间的关系为：
$$P_{O_R}=R{P}_{O_L}+t\text{\hspace{1em}(10)}$$

即：以$O_L$坐标系为参考，$O_R$经过运动$R$、$t$变换到$O_L$，那么原来在$O_L$坐标系下的点$P$在$O_R$坐标系下表示为$P_{O_R}=R{P}_{O_L}+t$。如果我们还知道相机与世界坐标系的变换关系$T$，就可以将$P_{O_L}$或$P_{O_R}$转换到世界坐标系下表示，得到点$P$的世界坐标。

三、PnP问题

  PnP（Perspective-n-Point）是根据图像中特征点的二维像素坐标及其对应的三维空间坐标，来估计相机在参考坐标系中位姿的一类算法。直观来讲，当相机观察到空间中的某一物体时，我们已经知道了该物体在某一参考坐标系下的位置和姿态，那么如何通过图片中物体的成像判断出相机此时在参考坐标系下的位姿？这正是PnP要解决的问题，即利用已知三维结构与图像的对应关系求解相机与参考坐标系的相对关系（相机的外参）。

  PnP是一类问题，针对不同的情况有不同的解法，常见的算法有：P3P、DLS、EPnP、UPnP等。

图3 PnP示意图

  如图3所示，考虑空间中某个点$P$，它在世界坐标系$O_w$中的齐次坐标为$P=[x,y,z,1{]}^{\text{T}}$，其投影到图像中的像素坐标为$p=[u,v,1{]}^{\text{T}}$。假设此时相机坐标系$O_c$与世界坐标系$O_w$之间的相对位姿关系由$R$、$t$来描述，则有：
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K\left[\begin{array}{cc}R& t\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\text{\hspace{1em}(11)}$$

其中的$R=\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& {\mathbf{r}}_3\end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$、$t=\left[\begin{array}{c}{t}_1\\ t_2\\ t_3\end{array}\right]$即为我们要求的旋转矩阵与平移向量，其实它俩就是所谓的相机外参。通过相机的外参可以将世界坐标系下的点转换到相机坐标系下表示，通过相机的内参可以将相机坐标系下的点转换到像素坐标系下表示。

  为了简化表示，我们暂时不考虑相机内参（因为内参$K$是已知且不变的），并令$T_{34}=\left[\begin{array}{cc}R& t\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]=\left[\begin{array}{cccc}{t}_{11}& t_{12}& t_{13}& t_{14}\\ t_{21}& t_{22}& t_{23}& t_{24}\\ t_{31}& t_{32}& t_{33}& t_{34}\end{array}\right]=\left[\begin{array}{c}{\tau }_1\\ {\tau }_2\\ {\tau }_3\end{array}\right]$，则上式可表示为：

$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{cccc}{t}_{11}& t_{12}& t_{13}& t_{14}\\ t_{21}& t_{22}& t_{23}& t_{24}\\ t_{31}& t_{32}& t_{33}& t_{34}\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}{\tau }_1\\ {\tau }_2\\ {\tau }_3\end{array}\right]P$$

  用最后一行把 $s$ 消去（$s={\tau }_{3}P$），得到两个约束：

$$u=\frac{{\tau }_{1}P}{{\tau }_{3}P}，v=\frac{{\tau }_{2}P}{{\tau }_{3}P}$$

于是有：

$$\{\begin{array}{l}{\tau }_{1}P-{\tau }_{3}Pu=0,\\ {\tau }_{2}P-{\tau }_{3}Pv=0.\end{array}\text{\hspace{1em}(12)}$$

  可以看到，每个特征点提供了两个关于 $T_{34}$ 的线性约束，而 $T_{34}$ 中有12个未知数，所以理论上至少需要6对匹配点就可以求出$T_{34}$ 。

四、ICP问题

  ICP（Iterative Closest Point）是根据前后两帧图像中匹配好的特征点在相机坐标系下的三维坐标，求解相机帧间运动的一种算法。直观来讲，当相机在某处观察某一物体时，我们知道了相机此时与物体之间的相对位姿关系；当相机运动到另一处，我们亦知道此时相机与物体的相对位姿关系，那么，如何通过这两次相机与物体的相对位姿关系来确定相机发生了怎样的运动？这正是ICP要解决的问题。

  在ICP问题中，图像信息仅仅用来做特征点的匹配，而并不参与视图几何的运算。也就是说，ICP问题的求解用不到相机的内参与特征点的像素坐标。

图4 ICP示意图

  如图4所示，设空间中一点$P$在相机坐标系$O_L$下的坐标为$P_{O_L}=[x_l,y_l,z_l{]}^{\text{T}}$，在相机坐标系$O_R$下的坐标为$P_{O_R}=[x_r,y_r,z_r{]}^{\text{T}}$，$O_L$经过运动$R$、$t$到达$O_R$，则$P_{O_L}$与$P_{O_R}$之间的关系为：
$$P_{O_L}=R{P}_{O_R}+t\text{\hspace{1em}(13)}$$

写成齐次变换的形式：
$$\left[\begin{array}{c}{x}_l\\ y_l\\ z_l\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\end{array}\right]\left[\begin{array}{c}{x}_r\\ y_r\\ z_r\\ 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}{x}_r\\ y_r\\ z_r\\ 1\end{array}\right]\text{\hspace{1em}(14)}$$

  由此可见，每一个点$P$可以得到3个约束，那么理论上至少需要4个点就可以求得相机的运动$R$、$t$。

五、总结

1、对极几何（2D-2D）利用两帧图像中$n$对特征点的二维像素坐标，估计相机的相对运动$R$、$t$，它一般只在单目SLAM初始化的时候用到。

2、三角测量利用两帧图像中匹配特征点的像素坐标以及两个相机之间的相对位姿，估计特征点的三维空间坐标，这在单目以及双目（多目）的SLAM中都非常重要。

3、PnP（2D-3D）利用图像中$n$对特征点的二维像素坐标和与之对应的三维空间坐标，估计相机在空间的位置和姿态，是最重要的一种位姿估计方法。

4、ICP（3D-3D）利用$n$对特征点在不同相机坐标系下的三维坐标，估计相机之间的相对位姿，适用于RGB-D SLAM和激光SLAM（从原理上来说）。

5、以上种种，要想得到正确的结果，前提是准确的特征匹配以及理想的相机内参（包括针孔模型参数和畸变参数）。然而事实上，我们得到的往往是有误差或者有噪声的结果，所以通常称前面的工作为前端，因为后面还有很多事情要做，那就是后端的优化——从混乱中找寻真理。