一种基于整数指令的小数进制转换算法(附mips源码)
目录
- 问题的提出
- 算法思路
- 算法伪代码
- 算法误差分析
- MIPS代码
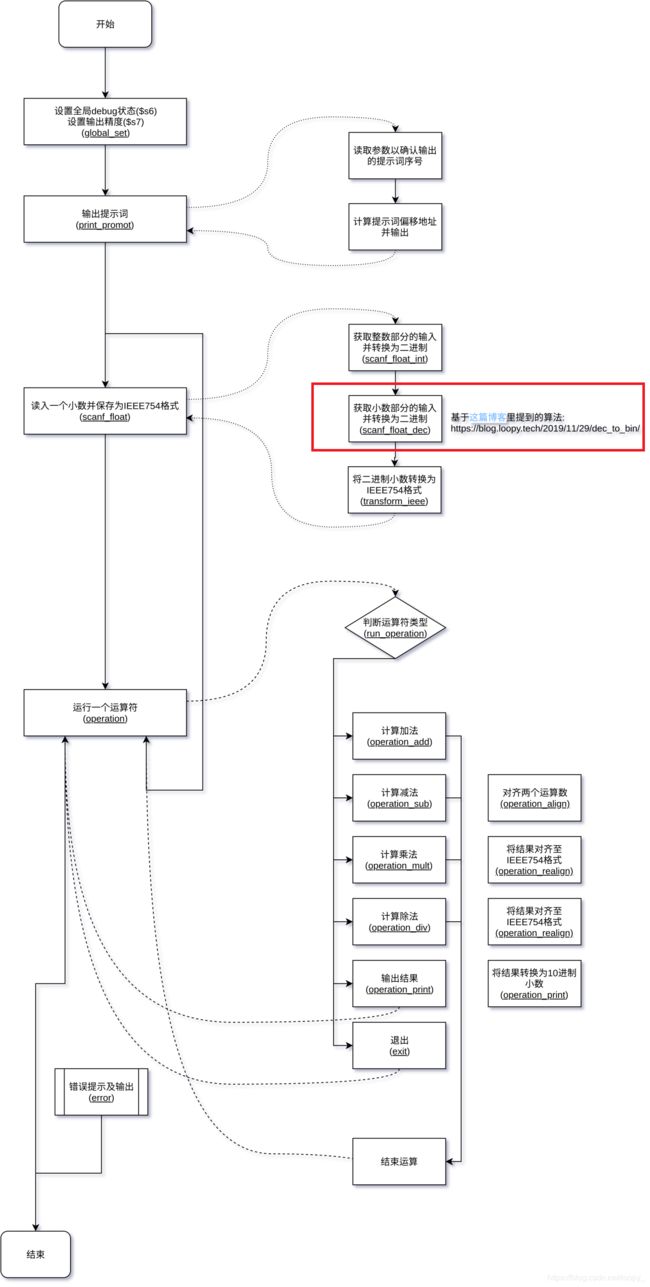
- 这个算法在整个流程里的位置
问题的提出
我的计组课设 - “浮点数的表示和计算”需要假设没有浮点表示和计算的硬件,用软件方法采用仿真方式实现IEEE 754单精度浮点数的表示及运算功能,其中关于二进制转十进制小数的部分比较困难, 查询资料也无果,于是我提出了这个算法,它的特点在于:
- 不使用浮点指令
- 算法中的所有变量都只能存储于32位的寄存器中
- 每读取一位小数,就将这位小数的信息表达到结果中,避免内存消耗
算法思路
这个算法基于上面特点中的第三条,即:每读取一位小数,就将这位小数的信息表达到结果中,结果寄存器一直表示在当前已知的部分小数位的情景下,对二进制小数的最大值的最大似然估计
- 当没读取小数时,结果寄存器为0 (即估计值为 2 32 2^{32} 232)
- 当读取了第一位小数(十分位),比如7,则坍缩一部分可能性,结果寄存器减去 2 32 10 × ( 9 − 7 ) \frac{2^{32}}{10} \times (9-7) 10232×(9−7)(即:已知十分位是7后,对最大值的估计值为0.79999…->0.8)
- 继续读入后面的小数位,并继续调整估计值直至最后一位,比如7,这时寄存器应该减去 2 32 1 0 n × ( 10 − 7 ) \frac{2^{32}}{10^{n}} \times (10-7) 10n232×(10−7)(即:已知最后一位是7后,对最大值的估计值为0.7…3)
算法伪代码
小数转换{
初始化结果寄存器为2^32
初始化下一位位权为2^32//10
开始循环{
读入一位数x,若无法读入则退出循环
将结果减去 (9-x)*位权
更新位权(整除10)
}
将结果删除一个满位权
}
算法误差分析
算法丢失精度主要发生在更新位权的时候,为了进一步提升精度,可以先计算乘法,后整除位权.但由于这时的第一位位权会超限,则将第一个抽出来单独以低精度方式运行,python写出来是这样的(为了测试批量测试误差):
def dec_to_bin(x):
x = str(int(x * 10 ** 20)).zfill(20) # 用于模拟小数的前20位读入
res = 2 ** 32
base = 2 ** 32 // 10
res -= base * (9 - int(x[0]))
for i in x[1:]:
res -= base * (9 - int(i)) // 10
base //= 10
res -= base
return res
以下为误差测试的源码,使用numpy产生1000000个浮点数并计算误差:
import numpy as np
# 无误差的将二进值结果转换回十进制,以计算误差
def bin_to_dec(bin_res):
dec_res = 0
r_base = 1
for i in bin(bin_res).split("b")[1].zfill(32):
r_base /= 2
dec_res += int(i) * r_base
return dec_res
y_true = np.random.random(1000000)
x_test = y_true.tolist()
y_test_bin = [dec_to_bin(i) for i in x_test]
y_test_dec = np.array([bin_to_dec(i) for i in y_test_bin])
print("平均误差:{}\n".format(np.abs(y_true - y_test_dec).mean()))
print("平均相对误差:{}".format((np.abs(y_true - y_test_dec) / test_y_true).mean()))
# 平均误差:2.1892651971158193e-09
# 平均相对误差:3.286203933410582e-08
MIPS代码
scanf_float_dec: # func (get:None)-(t1:float_dec_part)
li $t3, '\n'
li $t4, 429496729
li $t5, 57
# get a char
li $v0, 12
syscall
# res($t1) -= base($t4) * (9 - char($v0))
sub $v0, $t5, $v0
mult $t4, $v0
mflo $v0
sub $t1, $t1, $v0
# Update the estimate value accroding to https://blog.loopy.tech/2019/11/29/dec_to_bin/
dec_char_update_res: # loop (for all char in dec_part[1:-1])
# get a char
li $v0, 12
syscall
# break if get '\n'
beq $v0, $t3, dec_char_fix_last
# res($t1) -= base($t4) * (9 - char($v0)) // 10
sub $v0, $t5, $v0
mult $t4, $v0
mflo $v0
divu $v0, $t2
mflo $v0
sub $t1, $t1, $v0
# base($t4) //= 10
divu $t4, $t2
mflo $t4
j dec_char_update_res
dec_char_fix_last: # not a loop or func
# res($t1) -= base($t4)
subu $t1, $t1, $t4
jr $ra