上下文无关文法(context free grammar)
语法分析的数学基础。
正则语言不能描述所有的语言,因此引入上下文无关文法(注意它也不能描述所有的语言,只是相对正则语言,描述范围增大)
它的功能比RE和DFA要强许多,可以描述句子的结构!!!
对于嵌套结构,比如程序中的括号非常有用,上下文无关文法可以处理
文法四元组定义:
\(G=
之前用正则语言比较难以定义下面这个语言,但是现在用上下文无关语言,就很容易定义这个
CFG产生式如下形式:
变量—>(变量 |终结符)* 形式化:\(A->\alpha , A\sub V_N,\alpha\sub (V_T \cup V_N)^*\)
在使用上下文无关文法产生式的时候,名字"上下文无关"由来:
$S->0S1 ,S=>00S11 $ 替换的时候 对于S不用管S的左边0,右边1;而是直接替换(可以说产生式头的核心,其核心左右边有无东西,意义不大,不影响,因此可以忽略,认为左边产生式头只有一个)
对于\(0S->0S11\), 我们需要"瞻前顾后",只有字符串是0S的时候,才可以被替换为0S11;(产生式头不只一个核心,核心左右也有非常重要的字符,需要观察配对)
\(\{V_T=\{0,1\},V_N=\{S\},S,\{S->01,S->0S1\}\}\)
迭代式推导(间接推导):\(=>^*\)
上面\(E+E,a+E,a+E*E,a+1*E\) 含有非终结符的叫做句型;(语法单位与串的混合;全部变量,和全部终结符 也是特殊句型)
\(a+1*0\)不含有非终结符的 叫做句子。
————————————————————————————
\(w\) 是终结符号串,\(S\)是开始符号
\(G=
\(L(G)={w|S=>^*w,w\in V_T^*}\)
正则语言一定是上下文无关语言(可以由上下文无关文法强于正规文法的角度看)
实际应用(编程)中,可以对CFG进行扩充,最著名BNF范式:
\(::= , |,…(一到多),\) 正规式用 +,前面Lex还用花括号{1,2,3,4},不同规范定义一到多标准不一样,但是含义都一样。
BNF转CFG
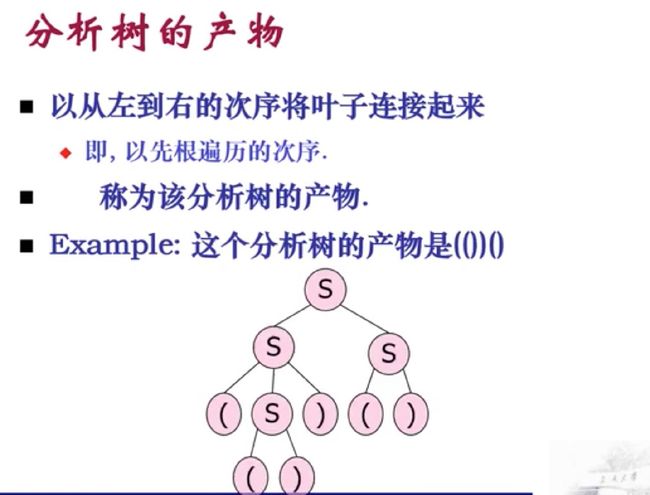
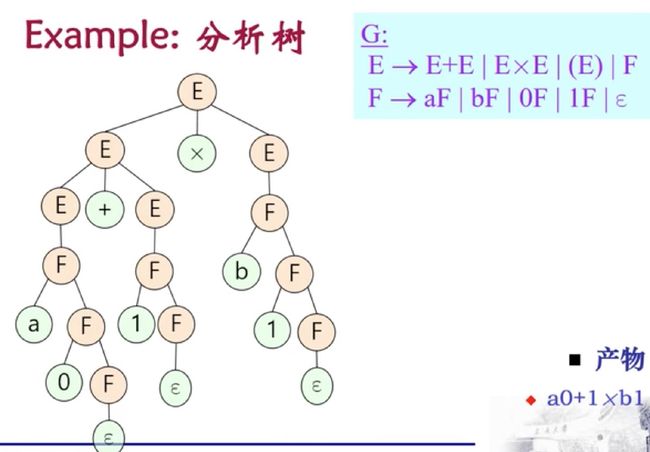
分析树:
二义性文法:存在一个串有多个语法分析树(大于等于2个)
等价定义:一个串有2个以上最左推导/最右推导
其实:每一个最左推导/最右推导 对应一个 语法树
二义性
等价定义
二义性是文法的性质不是语言的性质
二义性文法可以改造,改造之后可以消除二义性
为了避免随机选择候选式不成功引起回溯,我们采用"看当前输入串的第一个字符"的方式,根据这个字符再选择合适的候选式,这样就没有回溯了。
消除二义性算法
这样就不用找无二义性文法,即使没有二义性也能给它改造成无二义性
但是!!,有些文法 是必须有二义性的(固有二义性),这样我们就没办法了。
正规化上下文无关文法
面对二义性带来的不确定性,只要采用一套标准的正则化方法,就可以消除一部分二义性带来的问题。
对CFG化简步骤:
- 消除无用符号
- 消\(\epsilon\) 产生式
- 消产生式
- 对生成上面的生成式进行形式化
为什么要对CFG进行文法进行变换
由于原来的一般CFG,存在文法二义性,在推导的过程会引起回溯; 现在我们改造一下文法,让其推导过程没有回溯,而这个对产生式形式进行限制,就是我们的具体变换。使其变换后与原来可以达到相同的功能;另一方面,也可以简化文法,比如消除 \(A->\epsilon\)
- 生成式的标准形式 (1) Chomsky范式: \(A->BC,A->a,A,B,C\in V_N,a\in V_T\) (只有这两种产生式模子)
- (2) Greibash范式: 生成式形式为\(A->a\beta,a\in V_T,\beta\in V_N^*\) 对每个上下文无关语言都可以找到一个语言,使产生式右端都以终结符开始 (思想:消除左递归,只有一种模子)
标准化前预处理 消除无用符号
- 有用符号:符号既是 生成符号,又是可达符号 就叫做有用符号
S能够推导出来到X,然后由X能够推导到句子。我们就叫X做有用符号
- 无用符号:不是生成符号 | 不是可达符号
产生式如果存在无用符号,则该产生式就是无用的
我们的核心就是消去无用符号,消去无用产生式
步骤:
计算生成符号集
计算可达符号集
消去无用符号(含有不可达符号|不可生成符号)
消去相关无用产生式
- 生成符号集
先计算 是否生成符号**,不是生成符号再把这个不是的删去,相应的产生式也删去;再计算是否是可达符号,删去不死可达符号以及该可达符号相应的可达产生式
例题
可达的概念类似从头到尾,(开始符号一定是可达的)头是可达的,那么与头连接的紧接的尾就是可达的;
生成的概念从尾往前追溯,尾是生成的(终结符一定是可达的,最后的句子当然可达),与尾相紧接的前驱必然是生成的
消除\(\epsilon-产生式\)
对S分类别讨论,如果S是致空符号,那么引进新的开始符号\(S'\),\(引出两条产生式,S'->S,S'->\epsilon\)S ;如果S不是致空符号,基本不变,只是换一下符号\(S'—S,N'—N\) 。前提是判断一下所有变元(非终结符)是可致空的
Goals:语言里消去\(\epsilon\) \(L(G)=L(G_1)-\{\epsilon\}\)
其实就是消去含有e的产生式,需要注意得到上面有关产生e的产生式 的产生体得用\(\epsilon\)替换,将所有的可能都替换。找到所有的致空集合是关键。
消去单产生式(单位产生式)
\(A->B,B->C,C->D,D->xxx\) 本质上直接用\(A->xxx,B->xxx,C->xxx,D->xxx\) 可以直接代替
为什么要消去单位产生式??上面的文法功能是分析算符的优先级
但是发现 一个很简单的产生式 \(x\) 却 要经过E=>T=>F=P=id
太过于麻烦 要是消去上面我写的这种单产生式,就能很快的得到推导结果。
核心:从后往前代换即可
产生式体只有一个的直接代入替换即可 产生体不是单产生式的不能换。
\(A->B,A B都是非终结符\) 单产生式