KFDA的python实现
KFDA的python实现
- KFDA的Python实现
- 1.KFDA简介
- 2.二分类
- 3.多分类
KFDA的Python实现
1.KFDA简介
FDA是线性判断分析,是一种线性的有监督数据降维方法。其思想是最大化类间距和最小化类内距,找到最有利用分类的超平面对数据进行降维,再用分类方法对数据进行分类。与PCA不同,PCA是一种无监督数据降维方法。
PCA、FDA(或者叫LDA)都是一种线性降维方法,针对于非线性数据,降维后的数据用于分类效果很差,所以我们考虑引入核函数。通过某种映射,我们将低维空间的线性不可分数据映射到高维空间,原始数据在高维空间变成了线性可分的。但是在高维空间的样本数据在进行FDA降维时,会遇到两个样本的内积计算,由于原始样本已知,但是从低维空间到高维空间的映射未知,所以我们无法计算两个样本在高维空间的内积,此时核函数就派上了用场:将高维空间的样本的内积计算对应到低维空间样本的核函数计算。只要找到适合的核函数就能替代高位空间样本向量内积的计算。
如何找到等价的核函数呢?实际是存在这样的核函数的,如高斯核函数(又叫径向基核函数),多项式核函数,Sigmoid核函数等,具体理论说明请参考其他图书和文章。此处我们使用高斯函数,核函数选定后,核函数还有一个重要的参数——核参数,核参数对样本的投影后的样本分布影响很大,一般采用多次尝试的方法寻找适合的核参数。
文中的实现代码,都是本人经过矩阵公式推导得出的。
2.二分类
moons双月牙非线性数据是两类数据,对其进行KFDA降维,而后利用逻辑回归LR两类数据进行分类,然后利用区域内的所有样本点进行预测分类,绘制图的分类效果图,通过训练数据和测试数据的分类效果对模型有个初步认识。
1)原始数据样本分布
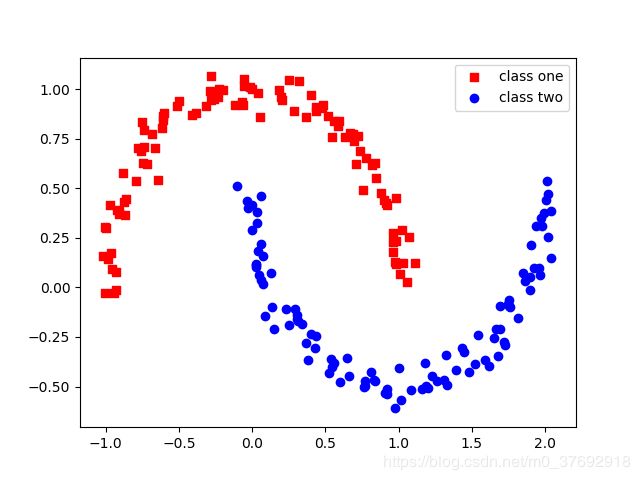
2)Python代码实现
KFDA.py 主程序代码:
import pandas as pd
from scipy.linalg import eigh
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import plot_decision_regions as pre
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
X, y = make_moons(n_samples =200,
noise=0.05,
random_state=1)
plt.scatter(X[y==0, 0], X[y==0, 1], c='red', marker='s',label='class one')
plt.scatter(X[y==1, 0], X[y==1, 1], c='blue', marker='o',label='class two')
plt.legend(loc = 'upper right')
plt.show()
##标准化
sc = StandardScaler()
X = sc.fit_transform(X)
##计算分子M矩阵,方式1;
def rbf_kernel_lda_m(X, gamma=0.01, c=0):
K_m = []
c_len = len([i for i in y if i==c])
for row in X:
K_one = 0.0
for c_row in X[y==c]:
K_one+= np.exp( -gamma*( np.sum( (row-c_row)**2 ) ) )
K_m.append(K_one/ c_len)
return np.array(K_m)
##计算M矩阵,方式2,结果同方式1
def rbf_kernel_lda_m_two(X, gamma=0.01, c=5):
N = X.shape[0]
c_len = len([i for i in y if i==c])
K_two = np.zeros((N,1))
for i in range( N ):
K_two[i,:] = np.array( np.sum( [ np.exp( -gamma*np.sum( (X[i]-c_row)**2 ) ) for c_row in X[y==c] ] ) )
return K_two/c_len
##计算N矩阵
def rbf_kernel_lda_n(X, gamma=0.01, c=5):
N = X.shape[0]
c_len = len([i for i in y if i==c])
I = np.eye( c_len )
I_n = np.eye(N)
I_c = np.ones((c_len,c_len))/c_len
K_one = np.zeros((X.shape[0],c_len))
for i in range( N ):
K_one[i,:] = np.array( [ np.exp( -gamma*np.sum( (X[i]-c_row)**2 ) ) for c_row in X[y==c] ] )
K_n = K_one.dot(I-I_c).dot(K_one.T) ##+ I_n*0.001
return K_n
##计算新样本点映射后的值;alphas 是其中一个映射向量
def project_x( X_new, X, gamma=0.01, alphas=[] ):
N = X.shape[0]
X_proj = np.zeros((N,1))
for i in range(len(X_new)):
k = np.exp( -gamma*np.array( [ np.sum( (X_new[i]-row)**2 ) for row in X ] ) )
X_proj[i, 0] = np.real( k[np.newaxis,:].dot(alphas) ) ##不能带虚部
return X_proj
for g_params in list([80,100,500]): ##14.52
N = X.shape[0]
##求判别式广义特征值和特征向量
K_m0 = np.zeros((N,1))
K_m1 = np.zeros((N,1))
K_m0 = rbf_kernel_lda_m(X, g_params , c=0)
K_m1 = rbf_kernel_lda_m(X, g_params , c=1)
K_m = (K_m0-K_m1)[:, np.newaxis].dot( (K_m0-K_m1)[np.newaxis, :] )
K_n = np.zeros((N,N))
for i in np.unique(y):
K_n += rbf_kernel_lda_n(X, g_params , c=i)
##方式1
from numpy import linalg
eigvals, eigvecs = np.linalg.eig( np.linalg.inv(K_n).dot(K_m))
eigen_pairs = [ (np.abs(eigvals[i]), eigvecs[:, i]) for i in range(len(eigvals)) ]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
alphas1 = eigen_pairs[0][1][:, np.newaxis]
alphas2 = eigen_pairs[1][1][:, np.newaxis]
##方式2
from scipy.linalg import eigh
eigvals1, eigvecs1 =eigh( np.linalg.inv(K_n).dot(K_m) )
eigen_pairs_one = [ (np.abs(eigvals1[i]), eigvecs1[:, i]) for i in range(len(eigvals1)) ]
eigen_pairs_two = sorted(eigen_pairs_one, key=lambda k: k[0], reverse=True)
alphas_one = eigen_pairs_two[0][1][:, np.newaxis]
alphas_two = eigen_pairs_two[1][1][:, np.newaxis]
#alphas1 = eigvecs1[-1][:, np.newaxis]
#alphas1 = eigvecs1[-2][:, np.newaxis]
##新样本点
X_new = np.zeros( (N,2) )
X_new[:, 0][:,np.newaxis]= project_x(X[:,:], X, g_params ,alphas1) #alphas_one,最佳参数gamma=14.52
X_new[:, 1][:,np.newaxis]= project_x(X[:,:], X, g_params ,alphas2) #alphas_two,最佳参数gamma=14.52
plt.scatter(X_new[y==0,0] ,X_new[y==0,1],c='red', marker='s',label = 'train one')
plt.scatter(X_new[y==1,0] ,X_new[y==1,1], c='blue', marker='o', label = 'train two')
plt.legend(loc='upper right')
plt.show()
##使用LR对样本进行分类
lr = LogisticRegression(C=1000, random_state=1,penalty='l1')
lr.fit(X_new,y)
##绘制决策边界
pre.plot_decision_regions(X_new, y,lr ,resolution=0.02)
plt.show()
plot_decision_regions.py绘制分类决策边界代码:
from matplotlib.colors import ListedColormap
import numpy as np
import matplotlib.pyplot as plt
def plot_decision_regions(X,y,classifier,resolution=0.0001):
markers=('s','x','o','^','v')
colors=('red','blue','lightgreen','gray','cyan')
cmap=ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:,0].min()-1, X[:,0].max()+1
x2_min, x2_max = X[:,1].min()-1, X[:,1].max()+1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))
Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1,xx2,Z,alpha=0.4,cmap=cmap)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
for idx ,cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl,0],y=X[y==cl,1],alpha=0.8,c=cmap(idx),marker=markers[idx],label=cl)
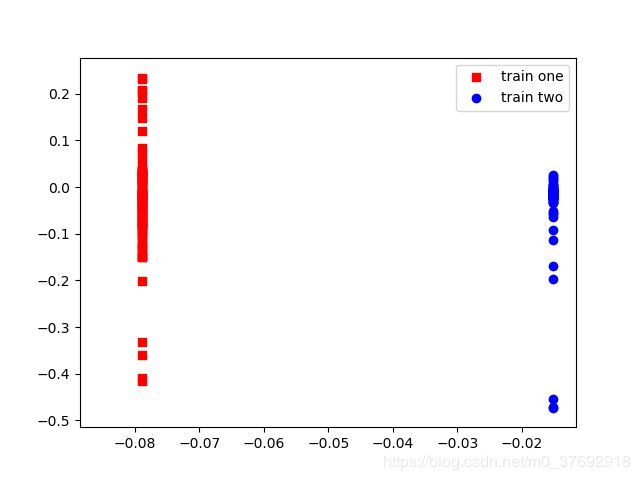
3)高维空间样本在KFDA投影向量上的数据分布
投影图:
核参数等于80时
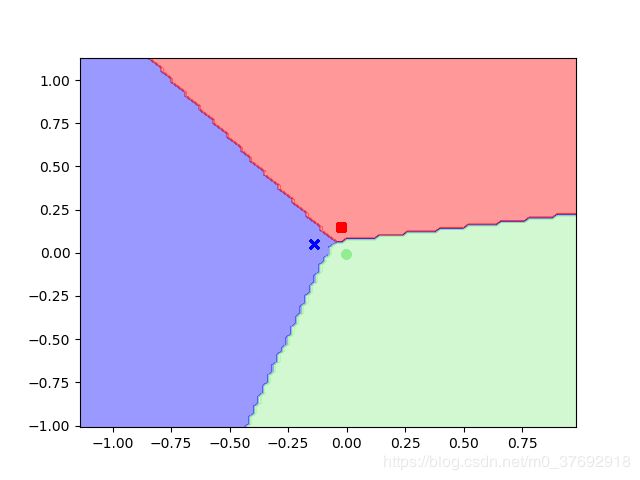
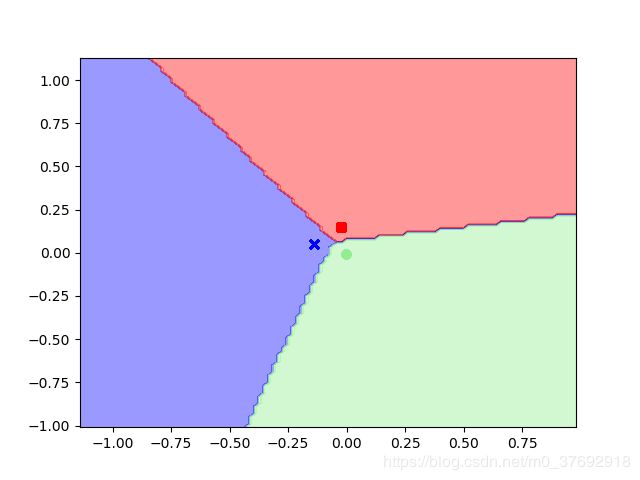
预测所有区域内样本类别,绘制决策边界:
核参数等于80时
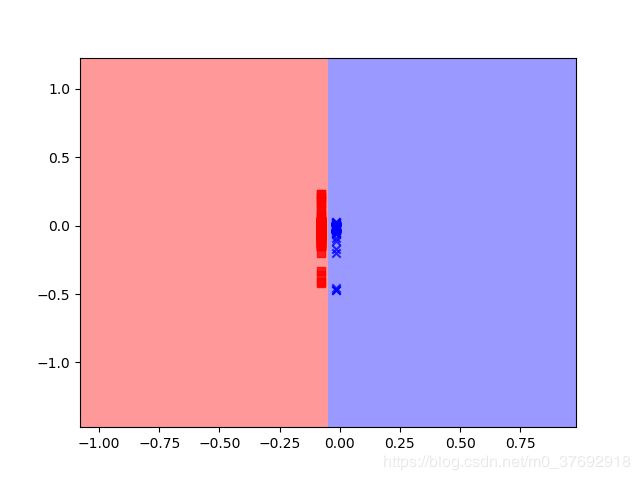
投影图:
核参数等于100时

预测所有区域内样本类别,绘制决策边界:
核参数等于100时
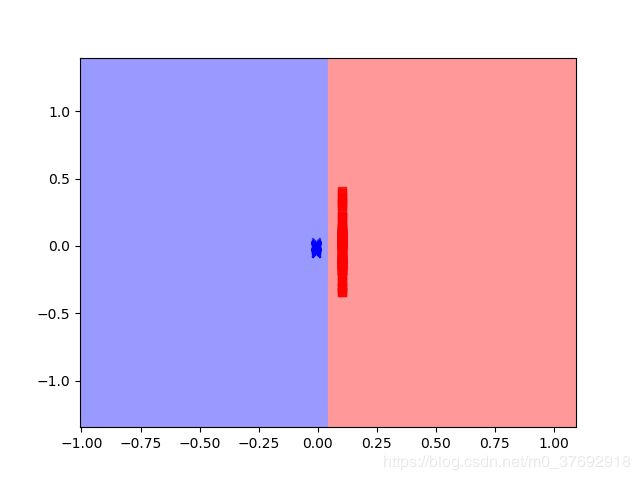
投影图:
核参数等于500时
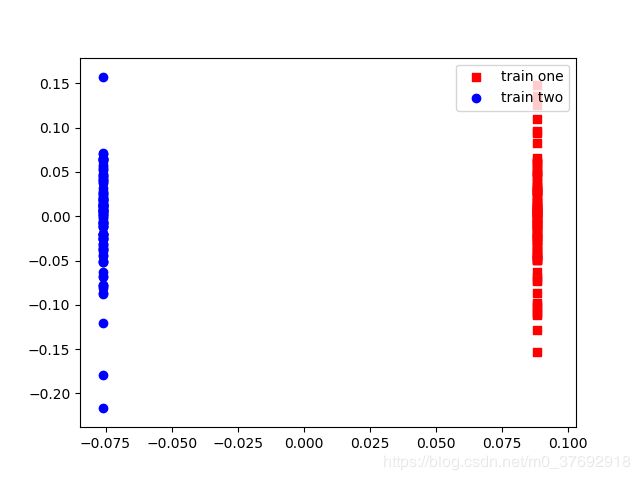
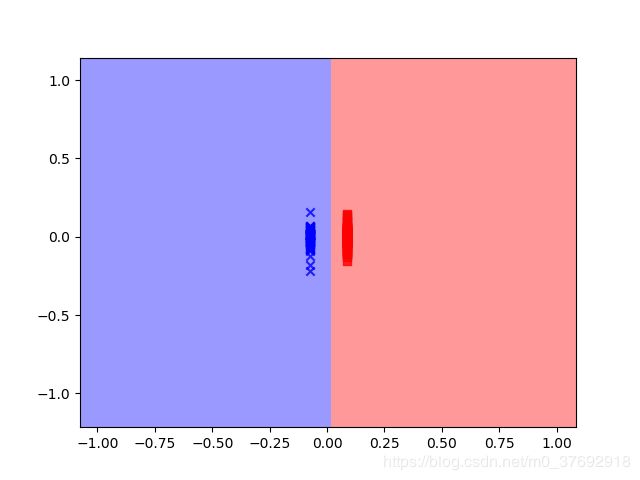
预测所有区域内样本类别,绘制决策边界:
核参数等于500时
3.多分类
使用wine_date数据集中的三类进行KFDA降维,然后绘制LR分类后的效果图,
1)原始数据样本分布

1)Python实现
wine_data数据集下载:参考其他链接。
wine_data_std.py啤酒数据集标准化代码:
import pandas as pd
df_wine = pd.read_csv('wine_data.csv')
##from sklearn.cross_validation import train_test_split
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X,y =df_wine.iloc[:,1:].values, df_wine.iloc[:,0].values
##X_train 123*13 ndarray , X_test 54*13 ndarray
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
sc = StandardScaler()
sc.fit(X_train)
X_train_std =sc.transform(X_train)
X_test_std = sc.transform(X_test)
KFDA_test.py代码:
import pandas as pd
from scipy.linalg import eigh
import numpy as np
import matplotlib.pyplot as plt
import plot_decision_regions as pre
from sklearn.linear_model import LogisticRegression
from itertools import combinations
from wine_data_std import *
##输入样本要求行排列
##计算分子M矩阵,方式1;
def rbf_kernel_lda_m(X, gamma=0.01, y=[]):
n = X.shape[0]
c_all = np.unique(y) #所有不重复类别
c_len = len(c_all) #类的数量
K_m = np.zeros( ( n, c_len) )
for k, c in enumerate(c_all):
c_len = len([i for i in y if i==c])
for i in range( n ):
K_val = 0.0
for c_row in X[y==c]:
K_val+= np.exp( -gamma*( np.sum( (X[i]-c_row)**2 ) ) )
K_m[i, k] = (K_val/ c_len)
M = np.zeros( ( n, n) )
for p in combinations( K_m.T, r=2):
M += (p[0]-p[1])[:, np.newaxis].dot( (p[0]-p[1])[np.newaxis, :] )
return M
##计算M矩阵,方式2,结果同方式1
def rbf_kernel_lda_m_two(X, gamma=0.01, y= []):
n = X.shape[0]
c_all = np.unique(y) #所有不重复类别
c_len = len(c_all) #类的数量
K_m = np.zeros( ( n, c_len) )
for k, c in enumerate(c_all):
for i in range( n ):
K_m[i, k] = np.array( np.sum( [ np.exp( -gamma*np.sum( (X[i]-c_row)**2 ) ) for c_row in X[y==c] ] ) )/c_len
M = np.zeros( ( n, n) )
for p in combinations( K_m.T, r=2):
M += (p[0]-p[1])[:, np.newaxis].dot( (p[0]-p[1])[np.newaxis, :] )
return M
##计算N矩阵
def rbf_kernel_lda_n(X, gamma=0.01, y = [] ):
n = X.shape[0]
c_all = np.unique(y) #所有不重复类别
##K_c = np.zeros((X.shape[0],c_len))
N = np.zeros( ( n, n) )
for k, c in enumerate(c_all):
c_num = len( [ i for i in y if i==c ] )
I = np.eye( c_num )
I_c = np.ones(( c_num, c_num ))/c_num
I_n = np.eye( n )
K_c = np.zeros(( n ,c_num ))
for i in range( n ):
K_c[i,:] = np.array( [ np.exp( -gamma*np.sum( (X[i]-c_row)**2 ) ) for c_row in X[y==c] ] )
N += K_c.dot( I - I_c ).dot( K_c.T ) ##+ I_n*0.001
return N
##计算新样本点映射后的值;alphas 是其中一个映射向量
def project_x( X_new, X, gamma=0.01, alphas=[] ):
n = X.shape[0]
X_proj = np.zeros( ( n, len( alphas )) )
for p in range( len(alphas) ):
for i in range(len(X_new)):
k = np.exp( -gamma*np.array( [ np.sum( (X_new[i]-row)**2 ) for row in X ] ) )
X_proj[i, p] = np.real( k[np.newaxis,:].dot( alphas[p]) ) ##不能带虚部
return X_proj
for g_params in list([500,1000]): ##14.52
X = X_train_std
y = y_train
p =2
n = X.shape[0]
##求判别式广义特征值和特征向量
##方式1计算K_m矩阵
K_m = rbf_kernel_lda_m(X, g_params , y)
##方式2计算K_m矩阵
##K_m = rbf_kernel_lda_m_two(X, g_params , y)
##方式1计算K_m矩阵
#K_n = np.zeros((N,N))
#for i in np.unique(y):
#K_n += rbf_kernel_lda_n(X, g_params , c=i)
K_n = rbf_kernel_lda_n(X, g_params , y)
##方式1
from numpy import linalg
eigvals, eigvecs = np.linalg.eig( np.linalg.inv(K_n).dot(K_m))
eigen_pairs = [ (np.abs(eigvals[i]), eigvecs[:, i]) for i in range(len(eigvals)) ]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
alphas1 = eigen_pairs[0][1][:, np.newaxis]
alphas2 = eigen_pairs[1][1][:, np.newaxis]
p = 2
alphas =[]
for i in range( p ):
alphas.append( eigen_pairs[i][1][:, np.newaxis] )
##方式2
from scipy.linalg import eigh
eigvals1, eigvecs1 =eigh( np.linalg.inv(K_n).dot(K_m) )
eigen_pairs_one = [ (np.abs(eigvals1[i]), eigvecs1[:, i]) for i in range(len(eigvals1)) ]
eigen_pairs_two = sorted(eigen_pairs_one, key=lambda k: k[0], reverse=True)
alphas_one = eigen_pairs_two[0][1][:, np.newaxis]
alphas_two = eigen_pairs_two[1][1][:, np.newaxis]
#alphas1 = eigvecs1[-1][:, np.newaxis]
#alphas2 = eigvecs1[-2][:, np.newaxis]
##新样本点
X_new = np.zeros( (n,p) )
X_new = project_x(X, X, g_params ,alphas )
plt.scatter(X_new[y==0,0] ,X_new[y==0,1],c='red', marker='s',label = 'train one')
plt.scatter(X_new[y==1,0] ,X_new[y==1,1], c='blue', marker='o', label = 'train two')
plt.scatter(X_new[y==2,0] ,X_new[y==2,1], c='green', marker='+', label = 'train three')
plt.legend(loc='upper right')
plt.show()
lr = LogisticRegression(C=1000, random_state=1,penalty='l2')
lr.fit(X_new,y)
pre.plot_decision_regions(X_new, y,lr ,resolution=0.02)
plt.show()