- 什么是Trie?
- 创建一棵Trie
- 向Trie中添加元素
- Trie的查询操作
- 对比二分搜索树和Trie的性能
- leetcode上的问题
什么是Trie?
Trie是一个多叉树,Trie专门为处理字符串而设计的。使用我们之前实现的二分搜索树来查询字典中的单词,查询的时间复杂度为O(logn),如果有100万(220)个单词,则logn大约等于20,但是使用Trie这种数据结构,查询每个条目的时间复杂度,和一共有多少个条目无关!时间复杂度为O(w),w为被查询单词的长度!大多数单词的长度小于10。
Trie将整个字符串以字母为单位,一个一个拆开,从根节点开始一直到叶子节点去遍历,就形成了一个单词,下图中的Trie就存储的四个单词(cat,dog,deer,panda)
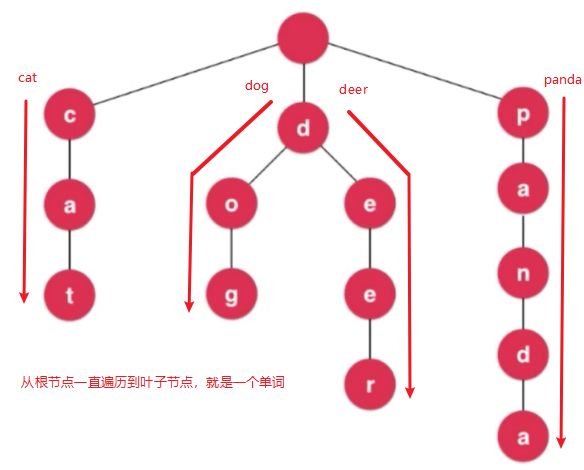
每个节点有26个字母指向下个节点的指针,考虑不同的语言,不同的情境,比如现在这个26个字符是没有包含大写字母的,如果需要包含大写字母,则需要让每个节点有52个指向下个节点的指针,如果现在要加入邮箱呢?所以这里描述为每个节点有若干个指向下个节点的指针。
由于很多单词可能是另外一个单词的前缀,比如pan就是panda的前缀,那么再Trie中如何存储呢?所以我们应该对节点添加一个标识符,判断该节点是否是某个单词的结尾,某一个单词的结尾只靠叶子节点是不能区别出来的,因此我们再设计Node节点时,应该添加一个IsWord,判断该节点是否是单词的结尾。
创建一棵Trie
在创建Trie之前,我们需要先设计Trie的节点类,根据上面说的,每个节点都有若干个指向下个节点的指针,还需要一个isWord来判断是否是单词的结尾,代码实现如下:
//设计Trie的节点类
private class Node{
//判断是否是一个单词
public boolean isWord;
//每个节点有若干个指向下个节点的指针
public TreeMap next;
//有参构造:对该节点进行初始化
public Node(boolean isWord){
this.isWord = isWord;
next = new TreeMap<>();
}
//无参构造:默认当前节点不是单词的结尾
public Node(){
this(false);
}
}
现在就让我们来实现一个Trie
public class Trie {
//设计Trie的节点类
private class Node{
//判断是否是一个单词
public boolean isWord;
//每个节点有若干个指向下个节点的指针
public TreeMap next;
//有参构造:对该节点进行初始化
public Node(boolean isWord){
this.isWord = isWord;
next = new TreeMap<>();
}
//无参构造:默认当前节点不是单词的结尾
public Node(){
this(false);
}
}
private Node root;
private int size;
public Trie() {
root = new Node();
size = 0;
}
// 获得Trie中存储的单词数量
public int getSize(){
return size;
}
}
向Trie中添加元素
Trie的添加操作:添加的是一个字符串,要把这个字符串拆成一个一个字符,把这一个一个字符作为一个一个节点,存入Trie中。
//向Trie中添加一个新的单词word
public void add(String word){
Node cur = root;
for (int i = 0 ;i < word.length(); i++){
//将这个新单词,拆成一个一个字符
char c = word.charAt(i);
//如果当前节点的若干个子节点中,没有存储当前字符的节点,则需要创建一个子节点,存储当前字符
if (cur.next.get(c) == null){
cur.next.put(c,new Node());
}
cur = cur.next.get(c);
}
//对添加的新单词遍历结束后,判断当前节点是否为单词的结尾,如果不是我们才对size加一,并且维护当前节点的isWord
if (! cur.isWord){
cur.isWord = true;
size ++;
}
}
Trie的查询操作
//Tire的查询操作
public boolean contains(String word){
Node cur = root;
for (int i = 0;i < word.length(); i++){
char c = word.charAt(i);
if (cur.next.get(c) == null ){
return false;
}
cur = cur.next.get(c);
}
return cur.isWord;
}
与查询类型,我们可以写一个是否存在以某个单词为前缀的单词
//查询在Trie中是否有单词以prefix为前缀
public boolean isPrefix(String prefix){
Node cur = root;
for (int i = 0; i < prefix.length(); i++){
char c = prefix.charAt(i);
if (cur.next.get(c) == null)
return false;
cur = cur.next.get(c);
}
return true;
}
对比二分搜索树和Trie的性能
这里对比二分搜索树和Trie的性能,仍然是使用的以添加和统计《傲慢与偏见》这本书为例,关于该测试用例中的文件工具类,和《傲慢与偏见》文档,请前往我之前写的 集合和映射 进行获取。
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
List words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)){
// Collections.sort(words);
long startTime = System.nanoTime();
//使用基于二分搜索树实现的集合进行添加和查询操作
BSTSet set = new BSTSet<>();
for(String word: words)
set.add(word);
for(String word: words)
set.contains(word);
long endTime = System.nanoTime();
double time = (endTime - startTime) / 1000000000.0;
//基于二分搜索树实现的集合进行添加和查询操作所花费的时间
System.out.println("Total different words: " + set.getSize());
System.out.println("BSTSet: " + time + " s");
// --- 测试通过Trie通过添加和查询所需要的时间
startTime = System.nanoTime();
Trie trie = new Trie();
for(String word: words)
trie.add(word);
for(String word: words)
trie.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("Total different words: " + trie.getSize());
System.out.println("Trie: " + time + " s");
}
}

通过上面测试代码可以看出,其实数据量不大的情况下,对于一个随机字符串的集合,使用二分搜索书和Trie进行添加和查询操作,差别是不大的,如果我们加入的数据是有序的,这时二分搜索树就会退化成链表,时间复杂度就为O(n),运行效率是很低的,但是Trie并不受影响,我们可以对words进行排序后,在看一下运行结果:
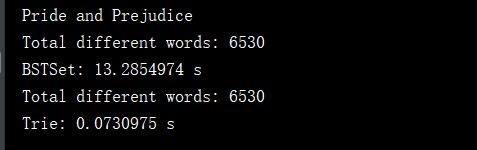
通过上面的测试,可以看出对有序的数据进行添加和查询操作,差距是特别大的。
leetcode上的问题
我们可以看到leetcode官网上的208好问题,就是实现一个Trie
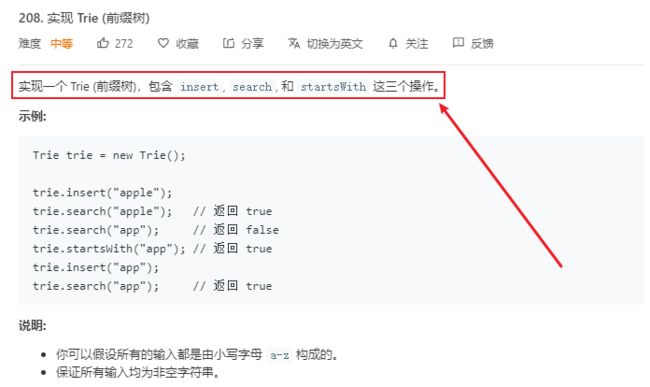
其实从题目描述中就可以看出,这个问题中的三个方法就是我们实现的add(),contains(),isPrefix()操作,直接将我们写的代码改个方法名字提交就可以通过了。

我们再来看一道leetcode上的211号问题:添加与搜索单词
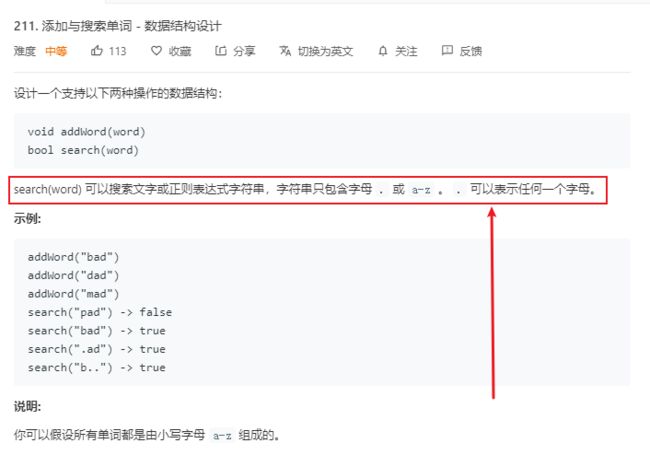
通过题目描述,我们会发现只是查询操作和我们实现的Trie有所不同,添加操作没有发改变。由于字符'.'可以代表任何一个字母,所以我们对于'.',需要遍历所有的可能。
public boolean search(String word) {
//递归匹配查找
return match(root,word,0);
}
private boolean match(Node node, String word, int index) {
if (index == word.length())
return node.isWord;
char c = word.charAt(index);
if (c != '.'){
if (node.next.get(c) == null)
return false;
return match(node.next.get(c),word,index+1);
}
else {
//如果当前节点的的值为‘.’,则需要遍历当前节点的所有子节点
for (char nextChar : node.next.keySet()) {
if (match(node.next.get(nextChar),word,index+1)){
return true;
}
}
return false;
}
}
代码提交到leetcode后,就会提示通过了

我们再来看看leetcode上的677号问题:Map Sum Pairs(键值映射)

根据题目描述,我们可以理解为:映射中存储的是单词和权重值。sum()方法是求得包含这个前缀单词得权重和
代码实现如下:
//设计节点类
private class Node{
//单词的权重值
public int value;
//每个节点都可能有若干个子节点
public TreeMap next;
public Node(int value){
this.value = value;
next = new TreeMap<>();
}
public Node(){
this(0);
}
}
private Node root;
public MapSum(){
root = new Node();
}
//添加操作和我们实现的字典树中的添加操作类型
public void insert(String word,int val){
Node cur = root;
for (int i = 0 ; i < word.length() ; i++){
char c = word.charAt(i);
if (cur.next.get(c) == null){
cur.next.put(c,new Node());
}
cur = cur.next.get(c);
}
cur.value = val;
}
//求前缀为prefix的权重和
public int sum(String prefix){
Node cur = root;
for (int i = 0 ; i < prefix.length() ; i++){
char c = prefix.charAt(i);
if ( cur.next.get(c) == null ){
return 0;
}
cur = cur.next.get(c);
}
return sum(cur);
}
private int sum(Node node) {
int res = node.value;
for (char c : node.next.keySet()) {
res += sum(node.next.get(c));
}
return res;
}