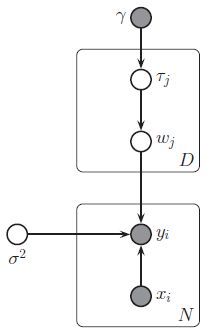
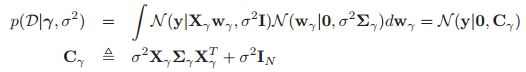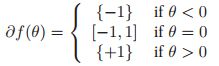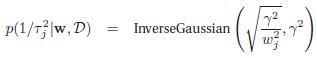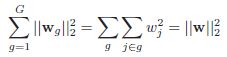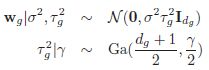MLAPP————第十三章 稀疏线性模型
第十三章 稀疏线性模型
13.1 简介
关于特征选择这个话题,其实我们在3.5.4中曾提到过,在那个方法中,我们会选择输入变量和输出的互信息很高的那些变量。这种方法的问题在于目光短浅,每次只关注一个变量。但是如果我们的变量相互之间是有联系的就不行了,比如说,如果![]() ,无论是
,无论是![]() 或者是
或者是![]() 都和结果的关系不是很大,但是异或的结果却和输出是一致的。
都和结果的关系不是很大,但是异或的结果却和输出是一致的。
在本章中,我们将着重于使用基于模型的方法一次性的选择一组变量。如果我们的模型是广义线性模型:![]() ,我们通过鼓励
,我们通过鼓励![]() 是稀疏的(有很多项是0)来进行特征的选择,这种方法提供了显著的计算优势,我们将在下面看到。
是稀疏的(有很多项是0)来进行特征的选择,这种方法提供了显著的计算优势,我们将在下面看到。
下面是特征选择/稀疏性非常有用的一些例子:
- 在许多问题中,我们的特征的数目D远大于我们的训练样本数N。对应的矩阵就是胖矩阵,而不是瘦矩阵。这个就叫做N小D大问题,这样的问题很容易导致过拟合。所以我们就要降低特征也就是D的数目。而且在这个时代这样的现象越来越多,因为我们的传感器越来越丰富,所能够获得的信息的维度越来越高。
- 在十四章中我们会讲到一个 sparse kernal machine 方法。
- 在信号处理中,常用小波基函数表示信号(图像、语音等)。为了节省时间和空间,找到信号的稀疏表示形式是有用的,这种稀疏表示形式是用少量的这种基函数表示的。这使我们能够从少量的测量中估计信号,以及压缩信号。13.8.3会进一步提到。
因此我们可以看到特征选择和稀疏性是当前机器学习/统计中最活跃的领域之一。在本章中,我们只对主要结果进行了概述。
13.2 贝叶斯变量选择
关于变量选择问题的一个很自然的想法就是引入隐变量![]() ,当
,当![]() ,我们就说第j个特征与输出是相关的,
,我们就说第j个特征与输出是相关的,![]() 则相反。那么我们模型的后验分布就是:
则相反。那么我们模型的后验分布就是:
其中![]() 称为代价函数(这里把
称为代价函数(这里把![]() 代入到上面的式子中就很容易看出来上面的式子是后验分布了):
代入到上面的式子中就很容易看出来上面的式子是后验分布了):
![]()
举个例子,假设我们从线性回归模型![]() ,其中
,其中![]() (特征的数目是10)以及
(特征的数目是10)以及![]() (
(![]() 其中有五个量是等于0),生成
其中有五个量是等于0),生成![]() 个样本。事实上,我们的
个样本。事实上,我们的![]() 以及
以及![]()
![]() 。很显然我们的模型有
。很显然我们的模型有![]() ,我们分别计算每一个的后验
,我们分别计算每一个的后验![]() ,我们用格雷码的方式对模型进行排序(相邻的编码只有一个bit是不一样的)。
,我们用格雷码的方式对模型进行排序(相邻的编码只有一个bit是不一样的)。
上图的左边是格雷码的编码方式,右边是模型的cost function![]() ,我们看到这个目标函数是非常颠簸的,如果我们计算模型的后验分布
,我们看到这个目标函数是非常颠簸的,如果我们计算模型的后验分布![]() ,结果更容易解释。
,结果更容易解释。
上图的左边就是后验分布,我们取后验值最大的前八个模型:
根据生成数据的模型,我们知道我们的真实模型其实是![]() ,但是特征3和8的系数相比于噪声而言是比较小的,所以这两个量就比较难以检测。如果我们有足够的数据的化,那么我们的结果就会收敛到真实的模型,但是对于有限的数据,通常会有相当大的后验不确定性。
,但是特征3和8的系数相比于噪声而言是比较小的,所以这两个量就比较难以检测。如果我们有足够的数据的化,那么我们的结果就会收敛到真实的模型,但是对于有限的数据,通常会有相当大的后验不确定性。
由于模型的数目太多了,所以用后验分布来解释会非常的complex,所以我们需要寻求一些统计量,一个比较自然的就是MAP估计,也就是得到后验的众数,但是这样的量会丢失掉模型的分布信息。所以另一种相对好一点的方法是中值模型(median model),其计算方法是:![]()
这需要计算后边缘包含概率:![]() ,上面的图(d)就是这个计算结果。我们看到,模型对包含变量2和6很有信心。如果我们将决策阈值降低到0.1,我们也会添加3和9。然而,如果我们想要捕获变量8,我们将会把5和7也加进来。关于这个折中在5.7.2.1中有讨论,画关于阈值的ROC曲线。
,上面的图(d)就是这个计算结果。我们看到,模型对包含变量2和6很有信心。如果我们将决策阈值降低到0.1,我们也会添加3和9。然而,如果我们想要捕获变量8,我们将会把5和7也加进来。关于这个折中在5.7.2.1中有讨论,画关于阈值的ROC曲线。
上面的例子说明了变量选择的黄金标准:但是往往我们的模型是稀疏的时候,D都是很大的,这就意味着我们要穷举![]() ,才能把后验分布计算出来,这是一个非常庞大的计算量,因此,我们将花费本章的大部分时间集中在算法加速上。但是在我们这么做之前,我们先解释上面例子的
,才能把后验分布计算出来,这是一个非常庞大的计算量,因此,我们将花费本章的大部分时间集中在算法加速上。但是在我们这么做之前,我们先解释上面例子的![]() 是如何进行计算的。
是如何进行计算的。
13.2.1 The spike(钉) and slab(厚板) model
我们知道后验正比于先验乘以似然:![]() ,我们先来看先验,然后再去看似然。一般来说,对于1bit的向量,我们使用如下的先验:
,我们先来看先验,然后再去看似然。一般来说,对于1bit的向量,我们使用如下的先验:
其中![]() 是每一个变量相关的可能性,其实就是稀疏性,越小越稀疏。那么我们的log似然具有如下的形式:
是每一个变量相关的可能性,其实就是稀疏性,越小越稀疏。那么我们的log似然具有如下的形式:
其中![]() 控制着模型的稀疏性。
控制着模型的稀疏性。
我们的似然函数可以写成如下的形式:
为了符号的简洁,我们假设假设数据的均值是0,这样![]() 这个先验就省去了均值参数。
这个先验就省去了均值参数。
我们先讨论先验![]() ,如果
,如果![]() ,说明特征j是不相关的,所以我们则希望
,说明特征j是不相关的,所以我们则希望![]() ,相反
,相反![]() ,我们则希望
,我们则希望![]() 是非0的。如果我们标准化输入(这里应该指输入的scalar都是一样的),那么我们的先验就是
是非0的。如果我们标准化输入(这里应该指输入的scalar都是一样的),那么我们的先验就是![]() ,
,![]() 表明我们希望相关变量的系数到底多大。综上,那么我们的先验如下:
表明我们希望相关变量的系数到底多大。综上,那么我们的先验如下:
第一项就是delta函数,表明在原点有个峰,对于第二项,如果![]() ,那么
,那么![]() 就会接近于均匀分布,可以被认为是一个恒定高度的平板,所以我们称之为spike and slab model。对于
就会接近于均匀分布,可以被认为是一个恒定高度的平板,所以我们称之为spike and slab model。对于![]() 这些特征,我们其实是完全可以扔掉的,所以似然可以改写为:
这些特征,我们其实是完全可以扔掉的,所以似然可以改写为:
其中![]() 。我们定义先验为
。我们定义先验为![]() ,其中
,其中![]() 是任意的正定矩阵(我们经常使用g-prior,即
是任意的正定矩阵(我们经常使用g-prior,即![]() ,ridge regression,可以用CV,经验贝叶斯,多层贝叶斯来估计g)。
,ridge regression,可以用CV,经验贝叶斯,多层贝叶斯来估计g)。
有了这些先验之后,我们就可以计算相应的边缘似然函数了,我们假设噪声方差是已知的,那么计算公式如下:
关于这个的计算,我们通过公式4.126可以得到。
如果噪声的方差是不知道的,那么我们可以通过积分的方式将其积掉。我们经常使用![]() ,这是方差的共轭先验,关于a和b 的选择可以参照
,这是方差的共轭先验,关于a和b 的选择可以参照![]() 。如果我们使用
。如果我们使用![]() ,那么这就是jeffrey‘s 先验
,那么这就是jeffrey‘s 先验![]() ,也就是无信息的先验。所以我们的最终积分后的边缘似然如下(具体可以参照
,也就是无信息的先验。所以我们的最终积分后的边缘似然如下(具体可以参照![]() ):
):
其中![]() 。
。
当我们的边缘似然并不能通过积分计算得到,即没有闭式表达式(比如我们使用logistic回归,或者非线性模型时),那么我们就使用BIC准则来做近似,具体形式如下:
其中![]() 是最大似然或者是ML的计算结果,当然是基于
是最大似然或者是ML的计算结果,当然是基于![]() 的。当然我们也可以把似然加上去,那么我们的目标函数就是:
的。当然我们也可以把似然加上去,那么我们的目标函数就是:
我们可以看到这里有两个惩罚项:一个是对于边缘似然的BIC近似,另一项则是由于先验导致的。当然很明显这两项可以合并的,所以我们就用![]() 来表示。
来表示。
13.2.2 从伯努利-高斯模型到 正则化
正则化
另一个我们有时会使用的模型如下:
在信号处理领域,我们叫这个为伯努利-高斯模型,尽管我们有时也称它为binary mask模型。
从参数模型上,我们好像觉得这个模型与之前的spike和slab模型是一样的,但是从概率模型来看这个并不是一样,在伯努利-高斯模型中,模型是![]() ,然而spike and slab模型是
,然而spike and slab模型是![]()
这个模型很有趣的就是他可以用来推导一个非贝叶斯的模型,而且在很多文献中都很常用,其实就是![]() 正则化。首先我们注意到联合的先验具有如下的形式:
正则化。首先我们注意到联合的先验具有如下的形式:![]() 。
。
因此我们的对数后验分布具有如下形式(非归一化的):
同样,我们可以把![]() 分割成两个部分,分别是
分割成两个部分,分别是![]() ,也就是0和非0的两个部分。因此
,也就是0和非0的两个部分。因此![]() 。现在我们考虑
。现在我们考虑![]() ,所以我们不正则化非零权值(这样就没有来自于由于BIC近似或者边缘似然导致的惩罚项)。那么目标就变成:
,所以我们不正则化非零权值(这样就没有来自于由于BIC近似或者边缘似然导致的惩罚项)。那么目标就变成:
这个和BIC的目标很像。
我们可以不去找比特向量![]() ,而是做如下的处理
,而是做如下的处理![]() ,这个称之为
,这个称之为![]() 正则化,这样,我们就把离散的优化问题转化为离散的优化问题。但是即使是做了这样的改变之后,仍然是不好处理的,因为我们的目标函数仍然是不光滑的,还是很难去优化。
正则化,这样,我们就把离散的优化问题转化为离散的优化问题。但是即使是做了这样的改变之后,仍然是不好处理的,因为我们的目标函数仍然是不光滑的,还是很难去优化。
13.2.3 算法
对于上面的算法,我们计算出了后验或者似然,但是模型的数目依然是![]() ,所以想找一个全局最优解是不可能的。所以,相反我们不得不求助于一些启发式的方法,将这个形式改变成其它的形式。关于每一个方法模型的搜索空间,以及空间里每个点的cost。那我们在每一个固定的模型都要计算最大似然或者是边缘似然即
,所以想找一个全局最优解是不可能的。所以,相反我们不得不求助于一些启发式的方法,将这个形式改变成其它的形式。关于每一个方法模型的搜索空间,以及空间里每个点的cost。那我们在每一个固定的模型都要计算最大似然或者是边缘似然即![]() 或者
或者![]() 。这有时称为包装器方法(wrapper method
。这有时称为包装器方法(wrapper method
),因为我们用一个通用的模型拟合的过程,对一堆模型进行搜索(这个解释自己都觉得怪怪的)。
为了提高包装方法的效率,能够快速的计算新的模型的cost function是很重要的。也就是说对于上一个模型![]() ,对于新的模型
,对于新的模型![]() ,我们能用更新的方法去算,而不是重新计算一边。因为
,我们能用更新的方法去算,而不是重新计算一边。因为![]() 和
和![]() 相比只有一个不同(要不然就是加一项,要不然就是减一项),具体的细节就先不谈,这要根据具体的情况推导。
相比只有一个不同(要不然就是加一项,要不然就是减一项),具体的细节就先不谈,这要根据具体的情况推导。
13.2.3.1 贪婪的搜索
假设我们希望发现MAP模型,如果我们使用![]() 公式,即
公式,即![]() 。我们可以利用最小二乘的性质,推导出各种有效的贪婪搜索方法,我们进行了如下的总结:
。我们可以利用最小二乘的性质,推导出各种有效的贪婪搜索方法,我们进行了如下的总结:
- Single best replacement:在这个方法中,对于
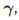 ,我们每一次翻转其中的一个,然后如果比之前的好,就替换掉,比如1000,我们就是先看0000和1000比哪个好,然后再看1100,1010,1001,最后找出这里面的最好的一个,作为新的。因为我们希望找到一个稀疏的解,所以我们一般初始化为
,我们每一次翻转其中的一个,然后如果比之前的好,就替换掉,比如1000,我们就是先看0000和1000比哪个好,然后再看1100,1010,1001,最后找出这里面的最好的一个,作为新的。因为我们希望找到一个稀疏的解,所以我们一般初始化为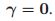 ,就这样不停的做,直到翻转每一个都不会提高性能为止。
,就这样不停的做,直到翻转每一个都不会提高性能为止。 - 正交最小二乘法(Orthogonal least squares):如果我们设定
 中的
中的 ,那么就没有关于模型复杂度的惩罚项了,那么这个时候我们就没有理由去delete某一项,所以其实在这个情况下,SBR就是正交最小二乘法。在这个算法下,我们同样初始化
,那么就没有关于模型复杂度的惩罚项了,那么这个时候我们就没有理由去delete某一项,所以其实在这个情况下,SBR就是正交最小二乘法。在这个算法下,我们同样初始化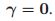 ,在每一步我们都加一项。那么在这个情况下,我们的error肯定是随着
,在每一步我们都加一项。那么在这个情况下,我们的error肯定是随着 单调下降,如下图:
单调下降,如下图:
我们增加的那一项![]() 必然是
必然是![]() ,然后更新为
,然后更新为![]() 。在这个方法下,我们第t步要计算
。在这个方法下,我们第t步要计算![]() ,其中
,其中![]() 。(我的疑问就是在这个方法中,我们怎么去找稀疏值呢,我们只是看到稀疏值对最终的影响,找拐点?)
。(我的疑问就是在这个方法中,我们怎么去找稀疏值呢,我们只是看到稀疏值对最终的影响,找拐点?)
- 正交匹配追踪(Orthogonal matching pursuits):正交最小二乘法凑从某种程度上说是计算复杂度较高的。所以我们提出一种新的方法,在每一次迭代的时候,我们固定
 不变,我们通过下面的式子来确定要添加哪一个变量:
不变,我们通过下面的式子来确定要添加哪一个变量:
其中![]() ,
,![]()
![]() ,这个优化问题更容易解决,因为
,这个优化问题更容易解决,因为![]() 是一个标量。并且如果每一列是单位范数的,我们有:
是一个标量。并且如果每一列是单位范数的,我们有:![]() ,我们可以看到这个式子就是找与当前的残差最接近的那一列。然后我们在利用正交最小二乘里面的式子使用
,我们可以看到这个式子就是找与当前的残差最接近的那一列。然后我们在利用正交最小二乘里面的式子使用![]() 去优化
去优化![]() 。这个方法就叫做正交匹配追踪法(orthogonal matching pursuits,OMP)。在这个方法当中,我们在每一个step只要进行一次最小二乘计算。
。这个方法就叫做正交匹配追踪法(orthogonal matching pursuits,OMP)。在这个方法当中,我们在每一个step只要进行一次最小二乘计算。
- 匹配追踪(matching pursuits):一个更加进攻性的方法,就是不管范数是否为1,直接就是找与残差最相关的那一列,这就是匹配追踪算法。这个方法等价于在16.4.6中讲的least square boosting。
- backwards selection:backwards selection以
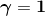 开始,然后在每一步中都删除掉最差的那一个。这相当于从格子的顶部向下执行贪婪搜索。这比自底向上的搜索可以得到更好的结果,因为是否保留变量的决策是在可能依赖于它的所有其他变量的上下文中做出的。但是对于大规模的问题,这个方法是不太可行的,因为对于稀疏模型来说,从上往下经历的步数要太多了。
开始,然后在每一步中都删除掉最差的那一个。这相当于从格子的顶部向下执行贪婪搜索。这比自底向上的搜索可以得到更好的结果,因为是否保留变量的决策是在可能依赖于它的所有其他变量的上下文中做出的。但是对于大规模的问题,这个方法是不太可行的,因为对于稀疏模型来说,从上往下经历的步数要太多了。 - FoBa:forwards-backwards algorithms跟single best replacement algorithms差不多,但是在进行选择的时候,它使用的是类似于OMP的优化准则(Zhang 2008)。
- 贝叶斯匹配追踪(Bayesian mathching persuit):这个OMP有点像,但是这里使用的是spike and slab模型中的贝叶斯边际似然的函数而不是最小二乘的目标函数。此外,它还使用了一种波束搜索的形式来同时探索通过晶格的多条路径。
13.2.3.2 随机搜索
如果我们希望得到的是后验分布,而不是mode。一个选择就是使用MCMC。标准的方法就是使用Metropolis Hastings(没听过)。这个可以通过![]() 得到
得到![]() ,具体就不去了解了。
,具体就不去了解了。
但是还有一种方法,叫做随机搜索算法,我么用:
对后验分布进行近似。
13.2.3.3 EM和变分推理*(这里就先看个大概,我也不是很懂)
我们可以尝试对spike and slab模型(![]() )使用EM算法。在E step的时候,我们可以计算
)使用EM算法。在E step的时候,我们可以计算![]() ,在M step的时候,我们去优化
,在M step的时候,我们去优化![]() 。但是这个实际并不可行,因为有一个delta函数,处理起来比较棘手,即使我们将其近似成高斯的,但是又会出现很多local点。
。但是这个实际并不可行,因为有一个delta函数,处理起来比较棘手,即使我们将其近似成高斯的,但是又会出现很多local点。
所以我们还是考虑对伯努利-高斯模型使用EM算法,其形式如下![]()
![]() 。在这个模型下,我们在E step需要计算
。在这个模型下,我们在E step需要计算![]() ,但是可以做近似
,但是可以做近似![]() 就可以做了。
就可以做了。
13.3.  正则化:基础
正则化:基础
当我们有很多的变量的时候,其实我们想要去计算后验![]() 的mode是非常的复杂的。尽管贪婪的算法经常work的很好,但是很多时候还是会卡在local optima上。
的mode是非常的复杂的。尽管贪婪的算法经常work的很好,但是很多时候还是会卡在local optima上。
为什么模型难以处理,一部分的原因就是变量![]() 是离散的。在优化的领域,针对离散变量,我们经常将其松弛成连续的变量。所以在spike and slab 模型中,我们将先验改成鼓励
是离散的。在优化的领域,针对离散变量,我们经常将其松弛成连续的变量。所以在spike and slab 模型中,我们将先验改成鼓励![]() 变成0的先验,所以这个先验在0处就会有一个很高峰。所以我们选择拉普拉斯分布作为先验,这在7.4节中讲rubust linear regression中提到过。考虑我们的先验具有如下的形式:
变成0的先验,所以这个先验在0处就会有一个很高峰。所以我们选择拉普拉斯分布作为先验,这在7.4节中讲rubust linear regression中提到过。考虑我们的先验具有如下的形式:
对于偏移常数项,我们就令它的先验是![]() 。所以我们的后验就是加了惩罚项的似然,具体如下:
。所以我们的后验就是加了惩罚项的似然,具体如下:
![]()
对于适当大的![]() ,
,![]() 将会是稀疏的。事实上这可以看作是对于一个非凸的问题(
将会是稀疏的。事实上这可以看作是对于一个非凸的问题(![]() )的一个凸近似。在线性模型中
)的一个凸近似。在线性模型中![]() 目标函数就变成了:
目标函数就变成了:
其中![]() 。这种方法称为基跟踪去噪或BPDN。其中
。这种方法称为基跟踪去噪或BPDN。其中
13.3.1 为什么 正则化能够得到稀疏的解?
正则化能够得到稀疏的解?
我们现在解释为什么![]() 正则化会导致稀疏的解,然而
正则化会导致稀疏的解,然而![]() 正则化却不能。尽管对于任何的GLMs都是可以的,但是我们这里还是关注于线性模型。我们的目标就是下面这个非光滑的目标函数:
正则化却不能。尽管对于任何的GLMs都是可以的,但是我们这里还是关注于线性模型。我们的目标就是下面这个非光滑的目标函数:
![]()
对于这个目标函数,我们可以写成有约束的,但是目标函数是光滑的形式:
![]()
很明显,如果B很小的化,就意味着我们的惩罚项![]() 很大。我们称这个式子为lasso,即least absolute shrinkage and selection operator(最小绝对收缩和选择算子),我们后面会看到为什么叫这个名字。
很大。我们称这个式子为lasso,即least absolute shrinkage and selection operator(最小绝对收缩和选择算子),我们后面会看到为什么叫这个名字。
类似的,我们也可以写出ridge regression 的形式:
下图我们给出了RSS分别在![]() 限制下和
限制下和![]() 限制下的最优解:
限制下的最优解:
我们可以看到左边的解是稀疏的,但是右边的解却不是(解就是等高线与蓝色区域第一次接触的点)。
或者我们换个角度,对于ridge regression来说,![]() 和
和![]() 对于先验的惩罚项其实是一样的,因为二范数的结果一样,但是对于lasso,
对于先验的惩罚项其实是一样的,因为二范数的结果一样,但是对于lasso,![]() 的1范数是要更小的。最严格的解释为什么是稀疏额方法是看在最优点的条件,后面我们就要说明这一点。
的1范数是要更小的。最严格的解释为什么是稀疏额方法是看在最优点的条件,后面我们就要说明这一点。
13.3.2 lasso 的最优性条件
lasso目标函数具有如下的形式:![]() ,不幸的是,
,不幸的是,![]() 在
在![]() 是不可导的。(
是不可导的。(![]() 和
和![]() 是一样的,书上没写好)这是一个非光滑的优化问题的一个例子。
是一样的,书上没写好)这是一个非光滑的优化问题的一个例子。
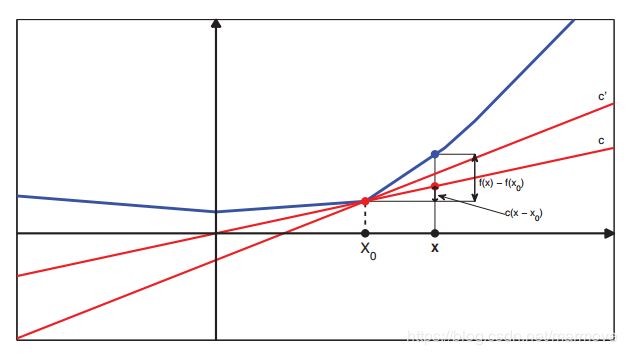
为了解决非光滑的函数,我们对梯度这个东西进行拓展。我们定义一个叫做次梯度的东西,对于一个函数![]() ,他在
,他在![]() 处的次梯度g必须满足:
处的次梯度g必须满足:![]() (对于向量就是
(对于向量就是![]() ),下图很好的阐述了这一点:
),下图很好的阐述了这一点:
所以说,对于次梯度而言,就是一个区间值,这个区间为![]() ,其中我们有:
,其中我们有:
![]() 就称为函数f在点
就称为函数f在点![]() 处的次梯度,记为:
处的次梯度,记为:![]() 。例如,对于绝对值函数
。例如,对于绝对值函数![]() 来说,它的次梯度就是:
来说,它的次梯度就是:
如果一个函数是处处可导的,那么它的梯度和次梯度就是一样的,即:![]() 。所以如果次梯度的区间里面包括0的化,那么就说明这个点也是一个local minimum。
。所以如果次梯度的区间里面包括0的化,那么就说明这个点也是一个local minimum。
下面我们把这个概念应用到lasso里面去。首先我们先考虑非光滑的项被扔掉的情况,即:
其中![]() 就表示第j个元素被扔掉了。我们可以看到
就表示第j个元素被扔掉了。我们可以看到![]() 表明的就是第j个特征
表明的就是第j个特征![]() 和残差项
和残差项![]() 之间的相关性。
之间的相关性。
我们把惩罚项也加上去,那么次梯度的结果就是:
我们可以换一种更加紧凑的表达形式:
因为是分段函数,所以对于不同的![]() ,那么我们的解
,那么我们的解![]() 是处于不同的位置的(总共有三个位置)。
是处于不同的位置的(总共有三个位置)。
所以我们的结果可以写成如下的形式:
其中![]() ,其中
,其中![]() 。这个称为soft thresholding。具体我们可以根据下图:
。这个称为soft thresholding。具体我们可以根据下图:
黑色的线是![]() ,对应的是least square的拟合值。红色的线是正则化的估计值,我们看到在
,对应的是least square的拟合值。红色的线是正则化的估计值,我们看到在![]() 或者
或者![]() 都shift了一定的值。
都shift了一定的值。
相反,我们还有一个叫做hard thresholding的策略,如下图:
这里同样我们还是设定![]() 的情况下,
的情况下,![]() 也是等于0。但是在这个区间外的值,并没有进行便宜操作。在soft thresholding 中,即使较大的系数也会向0靠拢,因此lasso其实是一个biased 估计器。这其实是并不可取的,因为对于似然来说,如果他要这个系数比较大的话,我们不应该强行去偏移它,这一点我们会在13.6.2中讨论。
也是等于0。但是在这个区间外的值,并没有进行便宜操作。在soft thresholding 中,即使较大的系数也会向0靠拢,因此lasso其实是一个biased 估计器。这其实是并不可取的,因为对于似然来说,如果他要这个系数比较大的话,我们不应该强行去偏移它,这一点我们会在13.6.2中讨论。
所以这里我们就理解了为什么叫lasso(最小绝对选择和收缩算子),因为它选择了变量的一个子集,并通过惩罚绝对值来缩小所有的系数。如果![]() ,我们就会获得OLS的解。如果
,我们就会获得OLS的解。如果![]() ,那么我们就会得到
,那么我们就会得到![]() ,其中
,其中![]() 。这个值的计算是根据算NLL的最优解就是
。这个值的计算是根据算NLL的最优解就是![]() ,即
,即![]() (就是从似然的角度看你的解就是0)。
(就是从似然的角度看你的解就是0)。
13.3.3 关于最小二乘,lasso,ridge和子集选择 的比较
的比较
下面我们通过将![]() 正则化和最小二乘,
正则化和最小二乘,![]() 正则化以及
正则化以及![]() 正则化进行比较,来进一步的去了解
正则化进行比较,来进一步的去了解![]() 正则化。为了简单起见,我们假设
正则化。为了简单起见,我们假设![]() 是标准正交的,即
是标准正交的,即![]() ,在现实中的数据肯定不可能是这样的,但是这样其实也有一定的道理。在这种情形下,RSS如下:
,在现实中的数据肯定不可能是这样的,但是这样其实也有一定的道理。在这种情形下,RSS如下:
我们可以看到,我们可以将![]() 的每一维都分开来写,所以我们可以对于每一项来写MLE或者MAP估计结果:
的每一维都分开来写,所以我们可以对于每一项来写MLE或者MAP估计结果:
- MLE:OLS的结果是
 ,其中
,其中 是
是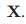 的第k列。
的第k列。 - Ridge:ridge的推导结果是(这个并不难,通过求导很容易)

- Lasso:根据书上的公式13.55,并且有
 ,我们有:
,我们有:
- 子集选择 :如果我们选择K个特征,那么我们的参数估计如下:
其中![]() 是指我们的这个w的排序在所有D个里面是排在前K个的,也就是找出前K个OLS最大的。其实这个就对应于我们的hard thresholding。
是指我们的这个w的排序在所有D个里面是排在前K个的,也就是找出前K个OLS最大的。其实这个就对应于我们的hard thresholding。
我们看下图
左边是lasso,MSE随着![]() 变化的情况,右边则是subset selection随着K的变化,我们可以看到这两个算法的性能是比较接近的。
变化的情况,右边则是subset selection随着K的变化,我们可以看到这两个算法的性能是比较接近的。
下面我们来看另一个例子,考虑一个关于前列腺癌的数据集。我们有![]() 个特征,以及
个特征,以及![]() 训练样本;目的是预测前列腺特异抗原的水平(比较专业了,不太懂),我们看下面这个表:
训练样本;目的是预测前列腺特异抗原的水平(比较专业了,不太懂),我们看下面这个表:
我们可以看到在这个数据集下,lasso的性能是最好的。对于稀疏的问题,一般来说lasso比较好,但是对于其它的一些,可能ridge更好,所以我们在后面13.5.3中会提到一个lasso和ridge结合的一个算法。
13.3.4 正则化路径(Regularization path)
随着我们增加![]() ,我们的解
,我们的解![]() 将会变的更加的稀疏,虽然这可能并不是单调的,但是整体趋势是这样的。我们可以对于每一个特征
将会变的更加的稀疏,虽然这可能并不是单调的,但是整体趋势是这样的。我们可以对于每一个特征![]() 画
画![]() 随着
随着![]() 。这个就是Regularization path。
。这个就是Regularization path。
对于ridge regression,如下图:
我们画了![]() 随着
随着![]() 减小的图像,我们可以看到随着
减小的图像,我们可以看到随着![]() ,所有的系数都将变成0。但是对于任何有限的
,所有的系数都将变成0。但是对于任何有限的![]() ,所有的系数都是非0的,随着
,所有的系数都是非0的,随着![]() 逐渐的减小,系数慢慢的增大。
逐渐的减小,系数慢慢的增大。
而对于lasso,我们看下图:
这里是随着B的变化。我们看到当![]() 的时候,所有的系数都是0,随着我们增加
的时候,所有的系数都是0,随着我们增加![]() ,这些被关闭的系数逐渐慢慢被开启。对于任何的
,这些被关闭的系数逐渐慢慢被开启。对于任何的![]() 在0到
在0到![]() 之间,解都是稀疏的。
之间,解都是稀疏的。
值得注意的是,求解路径是B的分段线性函数,即只要这个0-1的界限不发生改变,那么权重的改变就是线性的,具体如下图(a):
此外,还可以用解析法求解这些临界值。这是LARS算法的基础,表示least angle regression and shrinkage,具体在后面13.4.2提到。值得注意的是,LARS可以以与单个最小二乘拟合大致相同的计算成本计算整个正则化路径(![]() )。
)。
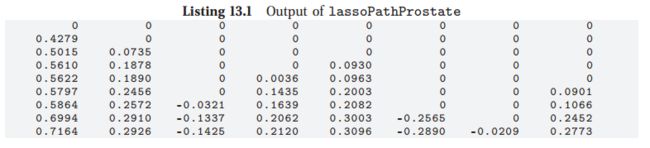
在上图(b)中,我们绘制了在每个临界值b处计算的系数。现在分段线性更加明显。下面我们显示正则化路径上每一步的实际系数值(最后一行是最小二乘解)
通过将B从0调到![]() ,我们可以看到解从全0到全不是0。就是如果在D>N的情况下,lasso最多也就之呢个有N个非0的项或者直接跳到OLS的解,关于这一点,我们后面会将一个将lasso和ridge结合起来的方法。叫做elastic net。
,我们可以看到解从全0到全不是0。就是如果在D>N的情况下,lasso最多也就之呢个有N个非0的项或者直接跳到OLS的解,关于这一点,我们后面会将一个将lasso和ridge结合起来的方法。叫做elastic net。
13.3.5 模型的选择
关于模型的选择,我们上面讲了用lasso去做,可以得到稀疏的解。实际上,在有些情况下,我们的真实的模型就是通过稀疏的![]() ,并且我们有相关的算法,能够真实的恢复出这个
,并且我们有相关的算法,能够真实的恢复出这个![]() (在
(在![]() ),我们称这个为模型选择一致性,具体的细节已经超出了本书的范围。
),我们称这个为模型选择一致性,具体的细节已经超出了本书的范围。
在这一小节中,我们并不会去进行理论的分析,只是举一些小的例子。我们的模型如下,首先![]() ,我们的
,我们的![]() 是在这4096个中选择160个空填1或者-1。然后我们生成N=1024的随机矩阵
是在这4096个中选择160个空填1或者-1。然后我们生成N=1024的随机矩阵![]() (
(![]() )。最后我们生成有噪的线性模型
)。最后我们生成有噪的线性模型![]() ,其中
,其中![]() ,我们要从
,我们要从![]() 估计
估计![]() 。
。
看下图:
第一行是真实的![]() ,第二行是利用lasso的结果,第三行是基于lasso估计出来的支撑集再利用最小二乘估计出来了,第三个就是直接利用最小二乘估计出来的。我们明显看到第三个的结果更加的好。直接用lasso,系数的大小相比于真实的偏小,而最后一个完全体现不了稀疏性。
,第二行是利用lasso的结果,第三行是基于lasso估计出来的支撑集再利用最小二乘估计出来了,第三个就是直接利用最小二乘估计出来的。我们明显看到第三个的结果更加的好。直接用lasso,系数的大小相比于真实的偏小,而最后一个完全体现不了稀疏性。
那么为了进行模型额选择,我们就要选一个合适![]() ,我们可以用cv来做,但是cv有一个问题,在cv中我们看重的是模型恢复的精度,但是这意味着,一个不太稀疏的模型,恢复的精度会更高,所以用cv可能并不是一个好的选择。在13.6.2中我们可能会讨论一个更好的办法。
,我们可以用cv来做,但是cv有一个问题,在cv中我们看重的是模型恢复的精度,但是这意味着,一个不太稀疏的模型,恢复的精度会更高,所以用cv可能并不是一个好的选择。在13.6.2中我们可能会讨论一个更好的办法。
使用![]() 还有一个问题就是不够robust,可能数据稍微改变一下,就会导致稀疏性的选择有很大的不同,而相比于这个而言,贝叶斯的框架就很robust。在频率派当中,去近似后验的一个方法就是用bootstrap 进行对数据集进行重复的采样,这样可以得到近似的分布,这个方法称之为 stability selection。
还有一个问题就是不够robust,可能数据稍微改变一下,就会导致稀疏性的选择有很大的不同,而相比于这个而言,贝叶斯的框架就很robust。在频率派当中,去近似后验的一个方法就是用bootstrap 进行对数据集进行重复的采样,这样可以得到近似的分布,这个方法称之为 stability selection。
对于上面的booststrap方法,我们可以找一个阈值,比如90%,那么对于变量如果在我们的booststrap中,90%的数据集的结果都有它的话,就保留,我们称这个方法是 bootstrap lasso或者是 bolasso(我们的估计器可以用固定![]() 的lasso)。有文章证明了,在某些条件下,bolasso相比于vanilla lasso(应该是指一般意义的lasso?)是model selection consistent的。书上举了一个例子,我们这里就不说了。
的lasso)。有文章证明了,在某些条件下,bolasso相比于vanilla lasso(应该是指一般意义的lasso?)是model selection consistent的。书上举了一个例子,我们这里就不说了。
在bolasso里面,很明显我们可以用cv来进行![]() 的选择。还有一些启发式的方法,但是都不太好。
的选择。还有一些启发式的方法,但是都不太好。
13.3.6 拉普拉斯先验的线性模型的贝叶斯推理
对于贝叶斯的角度来说,我们进行估计的时候可以取后验期望也就是mean,正常来说,后验的均值很有可能是不稀疏的,但是mode是稀疏的。但是用后验均值会使得均方误差更小,对于spike and slab模型,如果我们使用拉普拉斯先验,那么后验均值的效果会更加的好。
13.4  正则化:算法
正则化:算法
在这一节中,我们简要回顾了一些可以用来解决l1正则化估计问题的算法。我们这里关注于线性回归模型的lasso,当然其实这个算法也可以推广到GLMs。请注意,机器学习的这一领域发展非常迅速,所以当您阅读本章时,下面的方法可能还不是最先进的(的确如此)。
13.4.1 坐标下降法
有时很难同时对所有变量进行优化,但很容易逐一进行优化。实际上,我们可以在其它的坐标都固定的情况下优化第j个坐标:
其中![]() 就是第j个位置为1,其余位置为0的向量。我们可以以一种确定的方式对坐标进行循环,也可以对它们进行随机采样,或者我们可以选择更新梯度最大的坐标。
就是第j个位置为1,其余位置为0的向量。我们可以以一种确定的方式对坐标进行循环,也可以对它们进行随机采样,或者我们可以选择更新梯度最大的坐标。
如果每个一维优化问题都可以解析求解,那么坐标下降法就显得特别有吸引力。例如shooting algorithm(Wu and Lange 2008)就是这样的算法,伪代码如下:
在(Yaun 2010)中,将其应用到了logistic回归当中,该方法计算速度最快,对于稀疏性很强的特征有不错的效果。
13.4.2 LARS和其它同伦方法
但是坐标下降法针对不是稀疏度非常大的数据,由于其是一次只更新一个坐标,所以这种情况下,它的收敛速度就会很慢。Active set方法每次更新很多的变量,但是它们却更加的复杂,因为它们要去确认哪一些变量要设置为0,哪一些可以自由更新。
一般来说,active set的方法每一次只会增加或者减少一个或者说很少的变量,因此如果初始的支撑集合离真实的支撑集合很远的话,那么收敛需要很长的时间。但是这个算法非常适合用来生成一系列关于正则化参数![]() 的解(初始化变量集合是空集),例如我们之前讲得生成正则化参数。为什么这么说呢,因为这类算法挖掘出了一个非常好的性质,那就是如果
的解(初始化变量集合是空集),例如我们之前讲得生成正则化参数。为什么这么说呢,因为这类算法挖掘出了一个非常好的性质,那就是如果![]() ,我们可以基于
,我们可以基于![]() 很快的计算出
很快的计算出![]() ,这个被称之为warm starting。实际上即使我们只想知道一个具体的
,这个被称之为warm starting。实际上即使我们只想知道一个具体的![]() ,假设称之为
,假设称之为![]() 的具体的解,我们使用warm starting(这样的方法叫做continuation method or homotopy method,计算一系列的解从
的具体的解,我们使用warm starting(这样的方法叫做continuation method or homotopy method,计算一系列的解从![]() 到
到![]() ),这也比我们直接使用
),这也比我们直接使用![]() 作为初始值要快的多(cold starting),尤其是
作为初始值要快的多(cold starting),尤其是![]() 非常小的时候。
非常小的时候。
在机器学习领域最著名的homotopy method可能就是LARS方法,即:least angle regression and shrinkage。这个方法可以对于任何一个![]() 很快的计算
很快的计算![]() 。
。
LARS的具体工作如下:首先算法开始于![]() ,例如我们只能找到一个与观测
,例如我们只能找到一个与观测![]() 最相关的变量,然后我们不停的降低
最相关的变量,然后我们不停的降低![]() 直到第二个变量的出现,即第二个变量与残差的相关性和第一个变量相当(残差即为
直到第二个变量的出现,即第二个变量与残差的相关性和第一个变量相当(残差即为![]() ),然后我们可以通过几何的方法很快的把这个解给解出来。那么我们的正则化路径很容易就跳到了下一个点,重复这样的操作,知道所有的变量都被加进来。
),然后我们可以通过几何的方法很快的把这个解给解出来。那么我们的正则化路径很容易就跳到了下一个点,重复这样的操作,知道所有的变量都被加进来。
经过网上的相关搜索,所谓LARS其实就是我们书上的LAR,least angle regression,这样的方法于上面的有什么不同呢,其实我在网上都没有搜到least angle regression and shrinkage,所以有点不太明白。所以这里我就只关注于LAR了,那么上面的方法我觉得就是一个一个加变量,并没有涉及到变量的remove,所以感觉就是LAR,对于LAR来说,他的计算速度是非常快的,大概是![]() ,LAR的搜索方式有点像greedy forward selection,方法的话有点像后面16.4.6提到的least square boosting。
,LAR的搜索方式有点像greedy forward selection,方法的话有点像后面16.4.6提到的least square boosting。
有很多人尝试希望将LARS方法延伸到一般的GLMs的![]() 正则化模型当中去,比如说logistic回归等。对于这样的问题,同样针对一个特定的
正则化模型当中去,比如说logistic回归等。对于这样的问题,同样针对一个特定的![]() ,所以我们用之前提到过的warm starting,去搜寻path。在Friedman 2010这篇文章中结合坐标下降和warm starting来计算GLMs的
,所以我们用之前提到过的warm starting,去搜寻path。在Friedman 2010这篇文章中结合坐标下降和warm starting来计算GLMs的![]() 正则化模型的path,并实现在一个叫做PMTK的package中。
正则化模型的path,并实现在一个叫做PMTK的package中。
13.4.3 proximal 和梯度投影方法
在这一节中,我们将寻求解决大规模问题的方法,在这些问题中,之前讲的homotopy方法可能会显得比较慢。并且这一节的方法可以拓展到除了![]() 的其它正则化,这一节的展示主要是基于(vandenberghe 2011 Yang 2010)。
的其它正则化,这一节的展示主要是基于(vandenberghe 2011 Yang 2010)。
考虑一个具有如下形式的凸目标:
![]()
其中![]() 是loss function,是凸的并且是可微的,
是loss function,是凸的并且是可微的,![]() 是正则函数,也是凸的,但是并不需要一定是可微的。
是正则函数,也是凸的,但是并不需要一定是可微的。
例如![]() 和
和![]() ,这就对应于我们之前将的BPDN问题。书上还举了一个lasso的例子,虽然lasso的标准形式是带约束的优化问题,但是其本质和1范数正则化其实是一样的。
,这就对应于我们之前将的BPDN问题。书上还举了一个lasso的例子,虽然lasso的标准形式是带约束的优化问题,但是其本质和1范数正则化其实是一样的。
在某些简单的情况中,比如说,假设![]() ,并且
,并且![]() ,那么这个时候,我们的目标函数就是
,那么这个时候,我们的目标函数就是![]() 。关于这个的最小化,我们就称之为关于凸函数
。关于这个的最小化,我们就称之为关于凸函数![]() 的proximal 算子
的proximal 算子![]() ,定义如下:
,定义如下:
直觉上,我们就是要找一个既使得![]() 足够小,同时也非常靠近
足够小,同时也非常靠近![]() 的这样一个向量。一般的,我们在一个迭代算法里面用该算子,即我们希望变量离上次的结果不要太远,即
的这样一个向量。一般的,我们在一个迭代算法里面用该算子,即我们希望变量离上次的结果不要太远,即![]() 更新为:
更新为:
那么我们要解决的关键问题如下:对于不同的正则化![]() ,如何有效的计算proximal 算子,以及我们如何把这个方法拓展到更一般的损失函数
,如何有效的计算proximal 算子,以及我们如何把这个方法拓展到更一般的损失函数![]() ,下面我们将讨论这一点。
,下面我们将讨论这一点。
13.4.3.1 proximal 算子
如果有![]() ,那么proximal 算子的结果是(componentwise)
,那么proximal 算子的结果是(componentwise)![]() ,这一点根据13.3.2是很容易得到的,将
,这一点根据13.3.2是很容易得到的,将![]() ,并且
,并且![]() 正好对应一个0.5的系数关系。(注意,这一节的符号用的非常差,自己看的时候要对应好,
正好对应一个0.5的系数关系。(注意,这一节的符号用的非常差,自己看的时候要对应好,![]() 要对应好)
要对应好)
如果有![]() ,那么proximal 算子的最终结果是:
,那么proximal 算子的最终结果是:![]() ,其中
,其中![]() 。关于这个的证明:首先假设每一个component是独立的,我们就关注第i个元素,那么如果激活了,那么就会正则项就会有
。关于这个的证明:首先假设每一个component是独立的,我们就关注第i个元素,那么如果激活了,那么就会正则项就会有![]() 惩罚,这时候要使得最小,很明显这一项必然于上一次的结果一样即:
惩罚,这时候要使得最小,很明显这一项必然于上一次的结果一样即:![]() ,这样loss函数才没有惩罚,如果不被激活,正则项就没有惩罚,loss的惩罚就是
,这样loss函数才没有惩罚,如果不被激活,正则项就没有惩罚,loss的惩罚就是![]() ,所以到底激活与否就看
,所以到底激活与否就看![]() 和
和![]() 哪个大,所以就是书上的结果。
哪个大,所以就是书上的结果。
如果![]() ,那么proximal 算子的结果就是进行投影操作,即:
,那么proximal 算子的结果就是进行投影操作,即:
对于一些凸集,投影操作是很容易计算的。例如,我们我们投影到一个广义的矩形当中,即![]() ,投影的结果就是:
,投影的结果就是:
投影到欧几里得球![]() 上,投影的结果就是:
上,投影的结果就是:
投影到1-范数![]() 的球上,投影的结果就是:
的球上,投影的结果就是:
![]()
如果![]() ,那么就有
,那么就有![]() ,否则
,否则![]() 就是下面这个式子的结果:
就是下面这个式子的结果:
整个的过程只需要![]() ,具体的阐述在Duchi et al. 2008。
,具体的阐述在Duchi et al. 2008。
13.4.3.2 proximal 梯度方法(我觉得这个算法应该算是比较核心的部分)
我们现在讨论如何在梯度下降过程中使用proximal算子,我们的基本思想就是估计![]() 的时候将loss函数,通过泰勒展开成二阶近似的形式(在
的时候将loss函数,通过泰勒展开成二阶近似的形式(在![]() 这一点展开),具体公式如下:
这一点展开),具体公式如下:
其中![]() ,
,![]() 是一个常数,下面会讨论,但是基于的准则就是泰勒展开,即
是一个常数,下面会讨论,但是基于的准则就是泰勒展开,即![]() 。
。
扔掉那些与![]() 无关的项,然后在同时乘上
无关的项,然后在同时乘上![]() ,那么上面的目标函数就可以写成proximal 算子的形式,即:
,那么上面的目标函数就可以写成proximal 算子的形式,即:
如果![]() ,这个就等价于梯度下降法;如果
,这个就等价于梯度下降法;如果![]() ,该方法就等价于投影的梯度下降法,如下图:
,该方法就等价于投影的梯度下降法,如下图:
这幅图展示了投影梯度下降法的过程,首先计算没有投影的更新值,然后把该值投影到规定的集合中。如果![]() ,就是之前也提到过的iterative soft thresholding方法。
,就是之前也提到过的iterative soft thresholding方法。
那么关于![]() ,我们该怎么选择呢,我们换个符号表示,即
,我们该怎么选择呢,我们换个符号表示,即![]() ,我们之前讲过
,我们之前讲过![]() 是用来近似损失函数汉森矩阵的,即:
是用来近似损失函数汉森矩阵的,即:![]() ,根据最小二乘的结果,我们有:
,根据最小二乘的结果,我们有:
上面的这个近似方法,我们称之为Barzilai-Borwein (BB)或者是spectral stepsize(Barzilai and Borwein 1988; Fletcher 2005; Raydan 1997)。这样的步长选择不仅在我们这个proximal的背景下有用,对于一般的梯度下降法,我们也可以这样选步长,尽管这并不是关于目标函数单调下降的,但是相比于标准的line serach的方法(关于线搜索可以百度相关知识,线搜索是单调的)这个方法会更加的快。
当我们将BB stepwise和iterative soft thresholding(对于![]()
![]() )的方法结合起来,同时我们再加上一个连续修改
)的方法结合起来,同时我们再加上一个连续修改![]() 的方法,我们就能得到一个快速解决BPDN问题的方法,叫做SpaRSA(我们这里叫ISTA),具体伪代码如下:
的方法,我们就能得到一个快速解决BPDN问题的方法,叫做SpaRSA(我们这里叫ISTA),具体伪代码如下:
那么为什么这个方法更快呢,因为对于大量稀疏的数据,利用闭式表达式,要全算完,是非常的慢的,但是这个初始化为全为0的状态的话,其实是更快的,当然这是我个人的理解。
13.4.3.3 Nesterov’s method
刚才我们的proximal 梯度下降法是基于上一个时刻的![]() 进行泰勒的二阶展开,有一个更加快速的版本就是不是基于上一个时刻的点展开的,具体如下:
进行泰勒的二阶展开,有一个更加快速的版本就是不是基于上一个时刻的点展开的,具体如下:
这个被称为 Nesterov’s method。
同样基于这个框架,我们能够得到FISTA算法,唯一的区别就是展开的点的区别。算法还是参照上面的伪代码。
13.4.4 EM 算法应用到lasso
在这一节中,我们介绍如何用EM算法解决lasso问题。我们的第一直觉一定会有疑惑,因为在lasso里面并没有隐变量。但是我们注意到之前我们说过lasso等价于我们使用了拉普拉斯分布,而之前我们也讲过,拉普拉斯分布其实可以看成是高斯分布的一个混合,即:
这里的gamma分布就是指数分布,前面第二章有提到过,那么拉普拉斯就可以看作基于方差的这样一个求和。那么对应的lasso的概率图模型就是:
那么对应的联合概率分布就是:
其中![]() ,并且我们同时还假设了
,并且我们同时还假设了![]() 已经标准化了以及
已经标准化了以及![]() (这一点从上面的式子应该不难理解),下面我们将上面的式子进行展开:
(这一点从上面的式子应该不难理解),下面我们将上面的式子进行展开:
下面我们将具体的看EM算法的整个过程是怎么样的。简单点来说,我们在E step的时候,就是需要去推理![]() 以及
以及![]() ,而M step的时候,我们去估计
,而M step的时候,我们去估计![]() 。我们最终估计的结果,和lasso估计器估计出来的是一样的。
。我们最终估计的结果,和lasso估计器估计出来的是一样的。
13.4.4.1 为什么使用EM?
在我们详细介绍EM算法之前,我们有必要问一问,为什么我们已经提出了那么多解决lasso的方法,为什么我们还要用EM算法来做呢?原因是潜变量视角带来了几个优点,例如:
- 可以用该方法去解robust linear regression或者是probit regression
- 在这里我们lasso模型中,对于方差的先验是用的gamma分布,其实我们还可以用其它的分布,后面的拓展部分,我们会具体的讲到。
- 在这样的框架下不仅可以计算MAP估计,同时也提供了能够计算完整后验的思路,我们称之为贝叶斯lasso(具体可以参考 Park and Casella 2008; Hans 2009)
13.4.4.2 目标函数
根据书上的公式13.88,我们的log似然可以简化为如下的形式(把与![]() 无关的项扔掉):
无关的项扔掉):
其中![]() 是
是![]() 的精度矩阵。
的精度矩阵。
(这里我觉得有些困惑,首先我们其实是要计算联合似然或者后验分布关于隐变量后验分布的期望,在这里我们的后验分布是:
然后后面我们得到隐变量的后验分布是 ,这就有一个问题,因为这个分布就是跟
,这就有一个问题,因为这个分布就是跟![]() 相关的,所以其实上面直接就把后验分布中与
相关的,所以其实上面直接就把后验分布中与![]() 扔掉我觉得是不合适的,我个人觉得这是一种计算上的近似以及简化了)
扔掉我觉得是不合适的,我个人觉得这是一种计算上的近似以及简化了)
13.4.4.3 E step
在E step里面,我们的关键就是去计算![]() ,那么怎么做呢,我们基于书上的练习13.8进行相关的计算:
,那么怎么做呢,我们基于书上的练习13.8进行相关的计算:
实际上,我们也可以推导出完整的后验,具体见(Park and Casella 2008):
因此有:
令![]() 来记录E step的结果。
来记录E step的结果。
另外一方面,我们也要计算![]() 的后验分布,这个比较容易,只要利用共轭先验的知识,我们就可以得到:
的后验分布,这个比较容易,只要利用共轭先验的知识,我们就可以得到:
13.4.4.4 M step
在M step中,我们就是要计算![]() ,这其实就是高斯先验的MAP估计,所以结果是:
,这其实就是高斯先验的MAP估计,所以结果是:![]() 。但是由于我们希望很多的
。但是由于我们希望很多的![]() ,所以我们会有很多的
,所以我们会有很多的![]() ,这样就会导致
,这样就会导致![]() 在取逆的时候可能会产生数值不稳定的现象。庆幸的是,我们可以对
在取逆的时候可能会产生数值不稳定的现象。庆幸的是,我们可以对![]() 进行奇异值分解,即:
进行奇异值分解,即:![]() ,具体如下:
,具体如下:
其中:
13.4.4.5 Caveat(警告)
对于lasso这个问题来说,是一个凸问题,所以我们应该总是能找到全局最优解,但是实际上在EM算法中并不是这样,假设我们真实的解![]() ,但是呢,如果我们在M step中设定
,但是呢,如果我们在M step中设定![]() ,那么在E step中,我们继续会设定
,那么在E step中,我们继续会设定![]() ,那么在M step中我们又会设定
,那么在M step中我们又会设定![]() ,依次循环往复,我们就一直走不出来。幸运的是,在仿真中这样的情况并不多见。
,依次循环往复,我们就一直走不出来。幸运的是,在仿真中这样的情况并不多见。
13.5 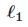 正则化:推广
正则化:推广
在这一节中,我们讨论关于标准的![]() 正则化的一些推广。
正则化的一些推广。
13.5.1 Group lasso
在标准化的![]() 正则化中,我们假设的是我们的参数和变量是一一对应的,所以如果说
正则化中,我们假设的是我们的参数和变量是一一对应的,所以如果说![]() ,那么我们的变量j就会被排除掉。但是在更加复杂的模型中,有可能对于一个变量我们有很多的参数和其相关。特别的,对于每一个变量j,我们有一个向量
,那么我们的变量j就会被排除掉。但是在更加复杂的模型中,有可能对于一个变量我们有很多的参数和其相关。特别的,对于每一个变量j,我们有一个向量![]() 来控制它。下面是一些具体的例子:
来控制它。下面是一些具体的例子:
- Multinomial logistic regression:每一个特征跟C个不同的权重系数相关,每一个对应一个类别。
- Linear regression with categorical inputs:Each scalar input is one-hot encoded into a vector of length C。
- 多任务学习:在多任务的学习中,我们可能有多个回归任务或者其它任务,对于不同的任务,我们的参数自然是不同的,但是我们的特征是一样的。
如果我们使用传统的![]() 正则化,即
正则化,即![]() ,那么我们的计算结果可能会导致
,那么我们的计算结果可能会导致![]() 中部分元素是0,这样的情况是需要避免的(这里我觉得如果对于多任务问题,其实某些任务是可以出现这样的情况的,这一点我并不理解我为什么要避免这样的情况,也许在有些应用中是要这样的)。
中部分元素是0,这样的情况是需要避免的(这里我觉得如果对于多任务问题,其实某些任务是可以出现这样的情况的,这一点我并不理解我为什么要避免这样的情况,也许在有些应用中是要这样的)。
基于上面的叙述,提出了这样的方法(后面会将一些东西表明为什么要这么干),我们将参数向量分成了G个组别。然后我们就要最小化如下的目标函数:
其中我们有:
如果NLL是最小平方的话,那么这个方法就称作group lasso。
对于更大的group,我们往往会使用更大的惩罚项,即![]() ,其中
,其中![]() 是group g中元素的个数。例如我们有两个group,即:
是group g中元素的个数。例如我们有两个group,即:![]() ,
,![]() ,那么目标就变为:
,那么目标就变为:
如果我们的惩罚项是二范数的平方的话,那么我们的模型就等价于ridge 回归了,由于:
通过使用平方根,我们正在惩罚包含组权重向量的球的半径:半径小的唯一方法是所有元素都很小。因此,平方根导致组稀疏性。
关于这个方法的一个变体就是将2范数替换为无穷范数,如下:
书上举了一个简单的例子,就是一个简单的线性模型,但是![]() 的维度很高,
的维度很高,![]() ,我们分别用标准的lasso和分成64组的group lasso以及无穷范数的group lasso。具体的图如下:
,我们分别用标准的lasso和分成64组的group lasso以及无穷范数的group lasso。具体的图如下:
这个图我们还不太能够看出group的优点,但是如果我们的![]() 生成是如下的方式,我们就很容易看出优势:
生成是如下的方式,我们就很容易看出优势:
13.5.1.1 group lasso的GSM解释
Group lasso 其实相当于对于如下的先验进行MAP估计:
而这个先验也可以写成GSM的形式,即:
其中![]() 是组别g的大小。我们可以看到,每一个group对应于一个方差,同时这个方差的先验是一个gamma先验,它的shape参数是由group的大小决定的,比例参数是由
是组别g的大小。我们可以看到,每一个group对应于一个方差,同时这个方差的先验是一个gamma先验,它的shape参数是由group的大小决定的,比例参数是由![]() 控制的。下图显示了之前的两个组别的例子的概率图模型:
控制的。下图显示了之前的两个组别的例子的概率图模型:
我们可以看到,这个GSM的参数相比于之前的拉普拉斯分布要更加的复杂,这也就体现了我们之前为什么要用EM去理解这个模型。
上图也一定程度上表明了这个算法为什么是叫做group的,因为我们可以根据图上看到,如果![]() 很小,那么就会导致
很小,那么就会导致![]() 很小,所以进一步
很小,所以进一步![]() 也会比较小,反之亦然,所以每一个组的权重大小是息息相关的。
也会比较小,反之亦然,所以每一个组的权重大小是息息相关的。
13.5.1.2 group lasso的算法
关于解group lasso问题,我们也有一些算法,下面我们简单介绍两个。第一个方法就是基于13.4.3讨论过的proximal gradient descent方法。因为我们的正则项是分开的,即![]() ,所以说我们的问题可以分解为G个完全不相关的独立的proximal 算子,即:
,所以说我们的问题可以分解为G个完全不相关的独立的proximal 算子,即:
其中![]() 。如果说
。如果说![]() ,(Combettes and Wajs 2005)可以表明,我们的proximal 算子就是
,(Combettes and Wajs 2005)可以表明,我们的proximal 算子就是![]() ,其中
,其中![]() 是一个二范数球。使用书上的公式13.74,如果
是一个二范数球。使用书上的公式13.74,如果![]() ,那么我们就有
,那么我们就有![]() ,否则的话,我们就有:
,否则的话,我们就有:
另一个方法就是EM算法了,因为我们刚才都说过group lasso的概率模型,而且是GSM的,所以利用EM算法是个不错的选择。这里方法基本上和标准的lasso没有什么本质区别,关于![]() 的更新跟之前是一摸一样的,没有区别,主要的区别就是后验更新,具体如下:
的更新跟之前是一摸一样的,没有区别,主要的区别就是后验更新,具体如下:
13.5.2 Fused lasso
在一些问题中呢,我们有两点希望,一个是希望相邻的系数之间会比较相似或者说接近,另外呢有大量的系数是稀疏的,根据这两点的要求,我们将会引出一个叫做fused lasso的模型,该模型的具有如下的先验:
为了展示的简单起见,我们就假设![]() ,我们的目标函数就可以写为(联合似然):
,我们的目标函数就可以写为(联合似然):
这里不知道为什么![]() 没了,可能计算消掉了,或者看作已知的了。
没了,可能计算消掉了,或者看作已知的了。
甚至这里我们鄙视基于链式的,而是基于一个更加复杂的图模型的,那么目标函数就是:
这个称之为graph-guided fused lasso。
13.5.2.1 用GSM去解释fused lasso
有人证明了,其实fused lasso 模型等价于如下的GSM,即:
其中![]() ,
,![]() 是一个三对角矩阵,其中:
是一个三对角矩阵,其中:
关于这个lasso本身,就简单说一下,大概知道有这么个方法,以及模型是什么样的,具体理解暂时就先不涉及了。
13.5.2.2 fused lasso的算法
可以用EM算法去做。
13.5.3 Elastic net(ridge 和 lasso 的结合)
尽管lasso作为变量的选择的一种方法,已经比较不错了,但是它还是会有一些问题,如下:
- 如果有一组变量,他们是高度的相关的,那么如果用lasso的话,我们可能只会选择其中的一个(可能是任意的一个)。事实上一个更好的解决方法是,我们知道这个模型的group情况,然后用group lasso去解会更好,但是事实上,我们并不知道这个group的结构。
- 如果说
 ,那么利用lasso的话,最多只能选择其中的N个变量。
,那么利用lasso的话,最多只能选择其中的N个变量。 - 而针对
 ,但是有很多的变量是相关的,我们经验的发现利用ridge回归的预测性能要比lasso的要好(这一点其实前面有说到过)。
,但是有很多的变量是相关的,我们经验的发现利用ridge回归的预测性能要比lasso的要好(这一点其实前面有说到过)。
Zou和Hastie提出了一种称为elastic net的方法,它是lasso和ridge回归之间的混合体,它解决了所有上面这些问题。
它之所以被称为“弹性网”,因为它“像一个可伸缩的渔网,保留了所有的大鱼”(Zou和Hastie 2005)。
13.5.3.1 标准的版本
在标准的版本下,定义的目标函数如下:
![]()
我们可以看到,这个函数是严格凸的(假设![]() ),所以其必然只有一个全局最优解。
),所以其必然只有一个全局最优解。
在Zou和Hastie 2005中,表明对于![]() 的严格凸的惩罚项会导致grouping effect,这意味这那些比较相关的系数,他们的对应的参数的估计值会比较接近。但是lasso完全不是这样,在lasso中,相关性很强的,只有一个能够留下来。
的严格凸的惩罚项会导致grouping effect,这意味这那些比较相关的系数,他们的对应的参数的估计值会比较接近。但是lasso完全不是这样,在lasso中,相关性很强的,只有一个能够留下来。
13.5.3.2 标准的elastic net的算法
我们通过比较简单的变量代换,很容易得到,其实elastic net可以被转化为lasso(当然数据不一样了)。具体定义如下:
其中![]() ,以及那么我们的问题就变为:
,以及那么我们的问题就变为:
![]()
最终的结果就是![]() 。
。
对于lasso问题,我们可以用LARS在解决这个问题,这个方法称作LARS-EN算法。如果我们在包括了m个变量之后就截至,那么代价就是![]() 。并且注意到在这个算法中,我们是可以选择D个的,因为
。并且注意到在这个算法中,我们是可以选择D个的,因为![]() 的秩是D。这一点就是我们之前说的第二个问题。
的秩是D。这一点就是我们之前说的第二个问题。
对于这个问题里面的![]() 和
和![]() ,可以用CV的方法去求解。
,可以用CV的方法去求解。
13.5.3.3 改进的版本
然而,我们发现。除非我们的模型非常接近纯的lasso或者ridge,标准的elastic net的效果并不好,直觉上来说就是收缩太多了,在2范数惩罚项中,我们需要收缩,在1范数惩罚项中又要进行收缩,所以在改进的版本中,我们对2范数这一块不进行收缩,我们的估计结果是![]() ,后面这个就是书上公式13.124的结果。我们称之为改正的估计。
,后面这个就是书上公式13.124的结果。我们称之为改正的估计。
其实我们对13.124进行展开,并稍做修改,那么我们改正的估计结果其实就是:
我们记![]() ,我们可以看到,其实我们就是把原来数据构成的协方差矩阵往单位阵上进行靠拢,看上去就是对协方差矩阵也进行了正则化。
,我们可以看到,其实我们就是把原来数据构成的协方差矩阵往单位阵上进行靠拢,看上去就是对协方差矩阵也进行了正则化。
13.5.3.4 elastic net 的GSM解释
在GSM概率模型下,elastic net 的先验模型很容易看出来就是:
就是一个高斯分布和拉普拉斯分布的乘积。同时在(kyung 2010)可以写成多层先验的形式:
同样我们可以通过EM算法来做。
13.6 非凸的正则化
尽管拉普拉斯先验最终是去解一个凸优化问题,但是从统计学的角度,这个先验并不是理想的。主要有两个问题,一个是在0这个点,它的概率密度还不够高,这就导致它并不能完美的抑制噪声。另一个问题就是它没有在大值上设置足够多的概率密度,所以相对于信号来说,它可能会导致相关系数的收缩。
那么要解决这个问题,我们就要找一个更加灵活的先验,该先验在0处有更高的峰,同时也有更重的尾巴。尽管在这种情况下,我们可能找不到全局最优解,只能找到局部最优的解,但是这种非凸的方法无论是在估计的精度还是检测相关的变量上面,都比使用拉普拉斯先验要好。下面我们给出一些例子。
13.6.1 Bridge回归
一个很自然的关于![]() 正则化的推广就是bridge regression(Frank and Friedman 1993),具有如下的形式:
正则化的推广就是bridge regression(Frank and Friedman 1993),具有如下的形式:
其中![]() 。这对应于我们进行MAP估计的时候使用exponential power distribution 作为先验,即:
。这对应于我们进行MAP估计的时候使用exponential power distribution 作为先验,即:
如果我们让b=2,那么这个分布就是高斯分布,对应于ridge回归。如果我们让b=1,那么这个分布就是拉普拉斯分布,对应于lasso回归。如果设定b=0,那就对应于![]() 回归。
回归。
而如果b<1,那么目标函数就不是凸的了,以及如果b>1,那么我们的目标函数就不会导致解是稀疏的。下图我们将展示不同的b所带来的不同的效果:
b分别等于2,1,0.4。并且我们假设![]() ,上面是先验的图形,后面是观察到一个数据的后验,我们可以看到ridge是没有稀疏性的,lasso有一个纵坐标的稀疏解,而b=0.4则对应于横坐标和纵坐标的两个稀疏解。
,上面是先验的图形,后面是观察到一个数据的后验,我们可以看到ridge是没有稀疏性的,lasso有一个纵坐标的稀疏解,而b=0.4则对应于横坐标和纵坐标的两个稀疏解。
13.6.2 多层的自适应lasso
我们之前讲过关于lasso的一个问题就是它的估计是有偏的,这是因为它要一个比较大的![]() 来保证解的一定稀疏性。但是这样的话也会影响到其余的权重的问题。所以可能我们对于不同的参数使用不同的惩罚参数可能会比较好。如果我们通过CV来确定这D个惩罚项参数的话,肯定是不现实的,但是在贝叶斯的框架下,这并不是什么难事,我们进行如下的概率模型的建立:
来保证解的一定稀疏性。但是这样的话也会影响到其余的权重的问题。所以可能我们对于不同的参数使用不同的惩罚参数可能会比较好。如果我们通过CV来确定这D个惩罚项参数的话,肯定是不现实的,但是在贝叶斯的框架下,这并不是什么难事,我们进行如下的概率模型的建立:
![]()
其概率图模型如下:
我们称这个模型叫做多层的自适应lasso模型(hierarchical adaptive lasso),这个方法的估计结果往往比直接用lasso要好,因为它不仅能够很好的挑选出合适的变量,并且估计的精度也非常的高。下面我们将将一下怎么用EM算法对这个模型进行估计。
13.6.2.1 将EM算法应用到HAL
由于我们知道,inverse Gamma 是拉普拉斯分布的共轭先验,所以在E step中,对于![]() ,我们的后验分布其实就是:
,我们的后验分布其实就是:
![]()
而在E step中,关于变量![]() 的估计是和标准的lasso是一样的。
的估计是和标准的lasso是一样的。
![]() 的先验具有如下的形式:
的先验具有如下的形式:
其实就是若干个拉普拉斯分布的相乘。
因此我们的M step就是去优化:
(这里类似于lasso EM中,把与![]() 无关的那些项全部扔掉了,所以剩下了这些项)
无关的那些项全部扔掉了,所以剩下了这些项)
所以我们的期望就是:
这一点其实并不是很难。
所以我们的M step就是变成了如下的问题:
这个书上写的也不对,对于![]() 求期望的这一项也丢了,不过只是在
求期望的这一项也丢了,不过只是在![]() 前面加一个常数项就好了。那么对于这个问题,我们就可以用标准的解lasso的方法去做(比如 LARS)。我们可以注意到如果上一次迭代估计出来的系数
前面加一个常数项就好了。那么对于这个问题,我们就可以用标准的解lasso的方法去做(比如 LARS)。我们可以注意到如果上一次迭代估计出来的系数![]() ,这个时候尺度因子
,这个时候尺度因子![]() 就会很小,所以很大的系数不会得到很大的惩罚。相反一样,上一轮估计出来很小的系数也不会被惩罚的很重,
就会很小,所以很大的系数不会得到很大的惩罚。相反一样,上一轮估计出来很小的系数也不会被惩罚的很重,![]() 最大也就是
最大也就是![]() 。所以在这个方法下,我们估计出来的结果往往都更加的稀疏同时偏差也更小。
。所以在这个方法下,我们估计出来的结果往往都更加的稀疏同时偏差也更小。
13.6.2.2 理解HAL的行为
如果我们将![]() 通过积分积没了,那么我们就可以得到如下的边缘分布:
通过积分积没了,那么我们就可以得到如下的边缘分布:
通过这种方式,我们能够更好的去理解HLA算法本身。这是一个广义t分布的一个例子,定义如下:
其中c是尺度参数(控制着稀疏度),a则是跟自由度相关的。当![]() ,就是对应着标准的学生t分布。当
,就是对应着标准的学生t分布。当![]() ,对应的就是指数幂分布。当
,对应的就是指数幂分布。当![]() ,我们就得到了拉普拉斯分布。在现在这个模型的背景下,其具体的参数对应着:
,我们就得到了拉普拉斯分布。在现在这个模型的背景下,其具体的参数对应着:
![]()
![]()
从这一点出发的话,我们的惩罚项就会具有如下的形式:
其中![]() 就是调整参数。我们可以画二维的图,具体如下:
就是调整参数。我们可以画二维的图,具体如下:
相比于书上的图13.3(a)的菱形图案,这个更像是一个star形状。这样的形状稀疏性要更加的强,但是这个很明显不是凸的。
好的,如果我们把上面这个引入到线性回归中,并且我们假设我们的设计矩阵![]() 是正交的。在这样的情况下,我们的目标函数就是:
是正交的。在这样的情况下,我们的目标函数就是:
其中![]() 以及
以及![]() ,这一点的话还是比较容易计算的。那么相应的我们的MAP计算结果就是:
,这一点的话还是比较容易计算的。那么相应的我们的MAP计算结果就是:
我们看下面的图:
左边就是两条线,虚线就是mle的结果,实线就是lasso的结果。而我们看右边的图就是HAL的结果。
13.6.3 其它多层的先验
另外我们还有很多促使稀疏的先验,具体如下表:
一个比较有趣的例子就是improper Nonmal-Jeffreys 先验。在这个模型中,对于方差我们使用了一个无信息的Jeffreys先验,其中![]()
![]() ,那么边缘的结果形式如下:
,那么边缘的结果形式如下:![]() 。
。
13.7 自动关联决策(Automatic relevance determination,ARD)/稀疏贝叶斯学习(Sparse Bayesian learning,SBL)
目前我们所考虑的这些方法关于![]() 的先验都具有如下的形式
的先验都具有如下的形式![]() (除了spike-and-slab 方法以外)。并且在之前的模型中,所有的先验都可以用GSM的方式来理解,即可以看成是若干个高斯分布
(除了spike-and-slab 方法以外)。并且在之前的模型中,所有的先验都可以用GSM的方式来理解,即可以看成是若干个高斯分布![]() 基于方差的混合,关于
基于方差的混合,关于![]() 的分布的具体形式可以看我们上面的表。
的分布的具体形式可以看我们上面的表。
通过引入这样的隐变量,我们的模型可以表示成如下的形式:![]() 。然后我们可以用EM算法进行MAP估计。在E step中,我们需要推理
。然后我们可以用EM算法进行MAP估计。在E step中,我们需要推理![]() ,在M step中,我们通过
,在M step中,我们通过![]() 以及
以及![]() 的分布来估计
的分布来估计![]() 。我们的混合其实不仅仅可以用高斯的,也可以用拉普拉斯的混合,这样在M step中对应的objective function 就会不一样。同时我们还会考虑使用贝叶斯推理的方法,而不是直接进行MAP估计。(当然其实我们的HAL并不是这样做的,在HAL中又引入了新的隐变量)。
。我们的混合其实不仅仅可以用高斯的,也可以用拉普拉斯的混合,这样在M step中对应的objective function 就会不一样。同时我们还会考虑使用贝叶斯推理的方法,而不是直接进行MAP估计。(当然其实我们的HAL并不是这样做的,在HAL中又引入了新的隐变量)。
在这一节中,我们使用第二类型的ML估计(经验贝叶斯),在该方法中,我们需要将![]() 通过积分积掉,然后最大化关于
通过积分积掉,然后最大化关于![]() 的边缘似然。我们下面将会将怎么去实现这一个过程。有了这个方差
的边缘似然。我们下面将会将怎么去实现这一个过程。有了这个方差![]() 的估计值之后,我们将其插入到后验分布中,通过计算后验分布权重
的估计值之后,我们将其插入到后验分布中,通过计算后验分布权重![]() 的均值,令人感到惊喜的是,最终的结果是稀疏的。
的均值,令人感到惊喜的是,最终的结果是稀疏的。
在神经网络的背景下,这个方法叫做自动关联决策(ARD),我们在这一章中只考虑线性模型,我们的方法就叫做稀疏贝叶斯学习(SBL)。通过将ARD\SBL的基函数进行拓展,会得到后面14章讲到的关联向量机器。
13.7.1 线性回归的ARD
我们这一章中,我们重点考虑的就是线性回归模型。将ARD应用到GLMs中,需要使用拉普拉斯近似。(关于拉普拉斯近似8.4.1讲到过,比较简单的版本就是将某个分布近似为高斯分布)当我们提到ARD\SBL时,我们就会进行如下的设定,即:
其中![]() ,
,![]() 以及
以及![]() 。那么我们的边缘似然可以通过如下的方式计算得到:
。那么我们的边缘似然可以通过如下的方式计算得到:
其中![]() 。
。
对于这个spike and slab模型中的边缘似然,即公式13.13,两者有很大的相似性。我们对目标取一个log,目标就变成了:
为了正则化这个问题,我们给每一个参数一个共轭先验,即![]() ,
,![]() 。那么调整过的目标就变成:
。那么调整过的目标就变成:
我们可以对参数![]() 进行贝叶斯推理分析。然而,如果我们使用点估计的话,我们就要使用improper的先验,即
进行贝叶斯推理分析。然而,如果我们使用点估计的话,我们就要使用improper的先验,即![]()
![]() ,这样的情况下,稀疏度是最大的。
,这样的情况下,稀疏度是最大的。
后面我们将会讲到如和去优化![]() 从而得到相应的估计值。这个模型从表面方法上其实是和spike and slab是非常像的,但是实际上,这个模型的local optimal点要比
从而得到相应的估计值。这个模型从表面方法上其实是和spike and slab是非常像的,但是实际上,这个模型的local optimal点要比![]() 目标函数要少很多,所以其实优化起来是更加简单的。
目标函数要少很多,所以其实优化起来是更加简单的。
一旦我们估计除了![]() ,那么我们就可以计算的到参数
,那么我们就可以计算的到参数![]() 的后验分布,即:
的后验分布,即:
我们计算![]() 的后验,同时鼓励稀疏性,这就是为什么这个方法叫做稀疏贝叶斯学习。尽管如此,由于有许多方法是稀疏的和贝叶斯的,所以即使在线性模型上下文中,我们也用ARD这个名称。
的后验,同时鼓励稀疏性,这就是为什么这个方法叫做稀疏贝叶斯学习。尽管如此,由于有许多方法是稀疏的和贝叶斯的,所以即使在线性模型上下文中,我们也用ARD这个名称。
13.7.2 什么时候稀疏?
如果![]() ,那么就相当于做最大似然估计
,那么就相当于做最大似然估计![]() ,因为高斯分布的精度参数趋向于0。但是如果
,因为高斯分布的精度参数趋向于0。但是如果![]() ,那么我们的先验就会非常的确定
,那么我们的先验就会非常的确定![]() ,因此我们的特征j就是不相关的。这样的话后验的均值就是
,因此我们的特征j就是不相关的。这样的话后验的均值就是![]() ,这样的情况下,不相关的参数就会完全被关闭。
,这样的情况下,不相关的参数就会完全被关闭。
下面我们基于Tipping 2001给出一个直觉上的感受,为什么在ML-Ⅱ中会鼓励不相关的特征的![]() 。考虑一个只有两个样本的一维的线性回归。即
。考虑一个只有两个样本的一维的线性回归。即![]() 。我们假设我们的特征与最终的
。我们假设我们的特征与最终的![]() 是不相关的,所以
是不相关的,所以![]() 的方向和
的方向和![]() 的方向是垂直的。那么当我们改变参数
的方向是垂直的。那么当我们改变参数![]() 时,我们下面来看一下边缘似然会怎么样。我们的边缘似然的具体形式是:
时,我们下面来看一下边缘似然会怎么样。我们的边缘似然的具体形式是:![]() ,其中:
,其中:
如果![]() 是有限的,那么我们的后验就是沿着
是有限的,那么我们的后验就是沿着![]() 方向的长椭形的。如下面的(a)图:
方向的长椭形的。如下面的(a)图:
然而如果![]() ,那么
,那么![]() ,
,![]() 就是一个球形的形状,如上面的(b)。如果
就是一个球形的形状,如上面的(b)。如果![]() 保持是一个常数的话,那么后者的话对于我们的观测到的向量
保持是一个常数的话,那么后者的话对于我们的观测到的向量![]() 会赋予更高的概率密度。所以这个解是更好的。
会赋予更高的概率密度。所以这个解是更好的。
13.7.3 与MAP估计之间的联系
ARD看上去跟我们这一章前面所学习的MAP方法有所不同。实际上,在ARD中,我们没有积分掉![]() 而去优化
而去优化![]() ,我们是恰恰相反的操作。这样做有什么好处呢,因为我们在进行
,我们是恰恰相反的操作。这样做有什么好处呢,因为我们在进行![]() 的估计时,我们使用的是所有特征的数据,并不仅仅是特征j,所以我们的
的估计时,我们使用的是所有特征的数据,并不仅仅是特征j,所以我们的![]() 就不是能像之前那样写成连乘的形式的,他是取决于所有数据
就不是能像之前那样写成连乘的形式的,他是取决于所有数据![]() 。在Wipf and Nagarajan 2007中,表明ARD可以写成如下的MAP估计问题:
。在Wipf and Nagarajan 2007中,表明ARD可以写成如下的MAP估计问题:
进一步,Wipf and Nagarajan 2007; Wipf et al. 2010证明了使用non-factorial的先验的MAP估计在某些方面要比使用factorial先验的MAP估计要好:non-factorial 目标总是比 factorial目标具有更少的local mnimum点,但是呢它的global optimum又和使用![]() 是一样的,而使用
是一样的,而使用![]() 正则化是达不到这样的效果的。
正则化是达不到这样的效果的。
13.7.4 ARD的一些算法*
在这一节中,我们回顾一下一些不同的算法来实现ARD。
13.7.4.1 EM算法
最简单的实现SBL\ARD算法的方法就是EM算法。期望完整数据的似然是:
其中![]() 是利用公式13.158计算得到的。这里因为
是利用公式13.158计算得到的。这里因为![]() 的后验分布是已知的,如公式13.156以及均值和方差都是已知的,所以直接带入计算就可以得到现在的结果。
的后验分布是已知的,如公式13.156以及均值和方差都是已知的,所以直接带入计算就可以得到现在的结果。
假设我们对于![]() 使用先验
使用先验![]() ,同时对
,同时对![]() 使用先验
使用先验![]() ,那么惩罚的目标函数就是:
,那么惩罚的目标函数就是:
如果![]() ,以及
,以及![]() ,那么更新就变成了:
,那么更新就变成了:
关于![]() 的更新如下:
的更新如下:
13.7.4.2 不动点算法(关于这个算法的推导我暂时还没有看懂,但是书上的结论肯定是有问题的)
一个更加快速和直接的方法就是直接去优化公式13.155的目标:
13.7.4.3 迭代再加权的![]() 算法
算法
13.8 稀疏编码*