一、定义
优先级队列有很多种实现方式。其中使用“堆”来实现“优先队列”是最常见的,堆的底层是完全二叉树的形式。
上述是一个小顶堆(最小堆)的示意图
最小堆是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。
二、API
2.1 上浮和下沉
堆的操作中,最重要的就是堆元素的上浮和下沉操作:
-
上浮(siftup)
在堆中插入元素后(完全二叉树的最右下方插入),需要进行上浮操作,重新使得堆有序。
private void swim(int k) {
while (k > 1 && (a[k]>a[k/2])) {
exch(k, k/2); //交换元素
k = k/2;
}
}
-
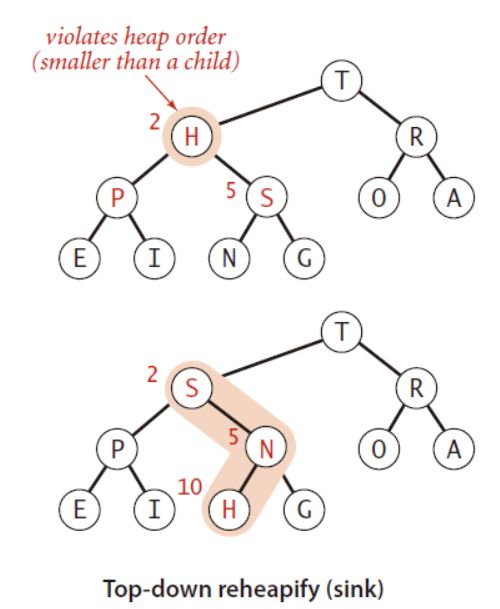
下沉(siftdown)
当删除一个堆元素(堆顶)时,首先将堆顶元素与最右下方元素交换,然后删除。此时堆顶元素需要进行下沉操作,重新使得堆有序。
private void sink(int k) {
while (2*k <= n) {
//j指向k的较小的子结点
int j = 2*k;
if (j < n && less(j, j+1)) j++;
if (!less(k, j)) break;
swap(k, j);
k = j;
}
}
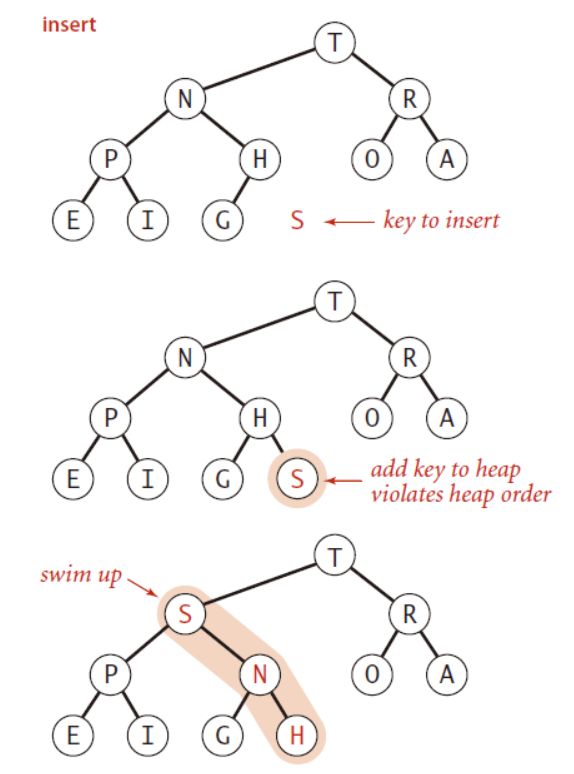
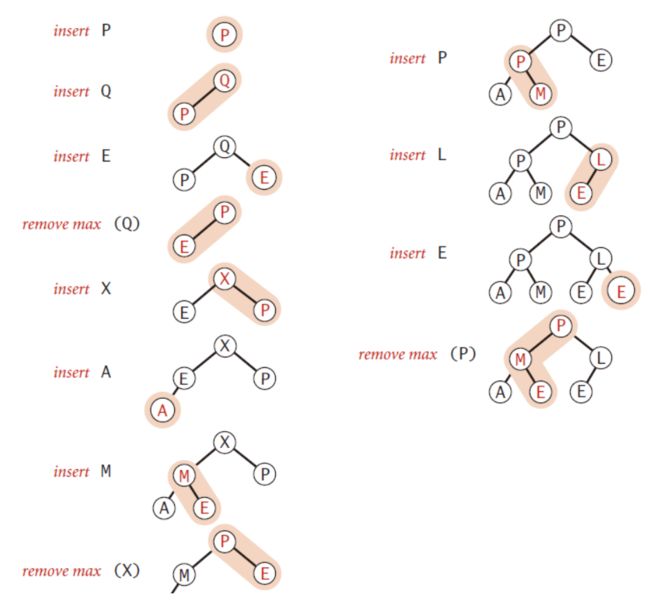
2.2 插入元素
新增元素添加到树的底层最右侧,然后上浮。
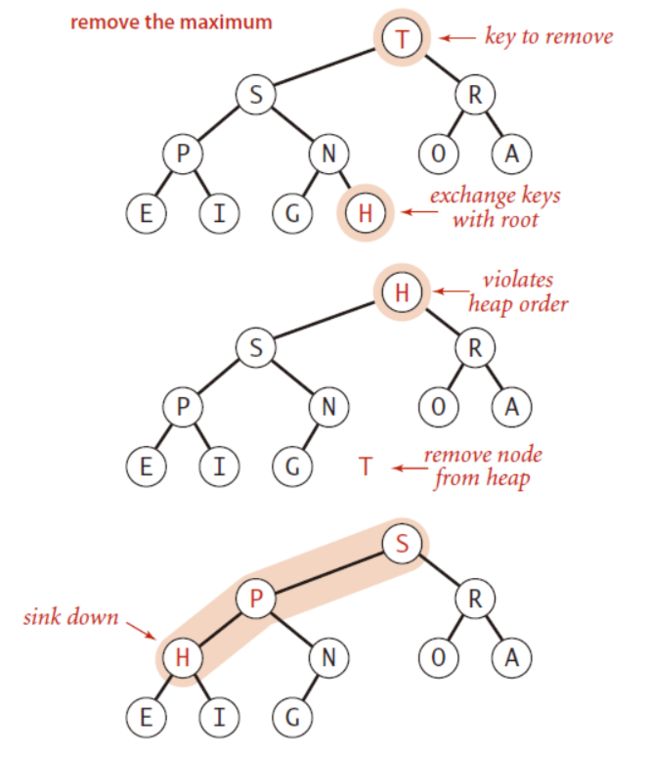
2.3 删除最大元素
将树的最后一个元素与第一个元素交换,删除最后一个元素,然后从堆顶开始下沉。
三、完整实现
3.1 大顶堆
public class MaxPQ implements Iterable {
private Key[] pq; // store items at indices 1 to n
private int n; // number of items on priority queue
private Comparator comparator; // optional comparator
/**
* Initializes an empty priority queue with the given initial capacity.
*
* @param initCapacity the initial capacity of this priority queue
*/
public MaxPQ(int initCapacity) {
pq = (Key[]) new Object[initCapacity + 1];
n = 0;
}
/**
* Initializes an empty priority queue.
*/
public MaxPQ() {
this(1);
}
/**
* Initializes an empty priority queue with the given initial capacity,
* using the given comparator.
*
* @param initCapacity the initial capacity of this priority queue
* @param comparator the order in which to compare the keys
*/
public MaxPQ(int initCapacity, Comparator comparator) {
this.comparator = comparator;
pq = (Key[]) new Object[initCapacity + 1];
n = 0;
}
/**
* Initializes an empty priority queue using the given comparator.
*
* @param comparator the order in which to compare the keys
*/
public MaxPQ(Comparator comparator) {
this(1, comparator);
}
/**
* Initializes a priority queue from the array of keys.
* Takes time proportional to the number of keys, using sink-based heap construction.
*
* @param keys the array of keys
*/
public MaxPQ(Key[] keys) {
n = keys.length;
pq = (Key[]) new Object[keys.length + 1];
for (int i = 0; i < n; i++)
pq[i+1] = keys[i];
for (int k = n/2; k >= 1; k--)
sink(k);
assert isMaxHeap();
}
/**
* Returns true if this priority queue is empty.
*
* @return {@code true} if this priority queue is empty;
* {@code false} otherwise
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Returns the number of keys on this priority queue.
*
* @return the number of keys on this priority queue
*/
public int size() {
return n;
}
/**
* Returns a largest key on this priority queue.
*
* @return a largest key on this priority queue
* @throws NoSuchElementException if this priority queue is empty
*/
public Key max() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
// helper function to double the size of the heap array
private void resize(int capacity) {
assert capacity > n;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= n; i++) {
temp[i] = pq[i];
}
pq = temp;
}
/**
* Adds a new key to this priority queue.
*
* @param x the new key to add to this priority queue
*/
public void insert(Key x) {
// double size of array if necessary
if (n == pq.length - 1) resize(2 * pq.length);
// add x, and percolate it up to maintain heap invariant
pq[++n] = x;
swim(n);
assert isMaxHeap();
}
/**
* Removes and returns a largest key on this priority queue.
*
* @return a largest key on this priority queue
* @throws NoSuchElementException if this priority queue is empty
*/
public Key delMax() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];
exch(1, n--);
sink(1);
pq[n+1] = null; // to avoid loiterig and help with garbage collection
if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
assert isMaxHeap();
return max;
}
/***************************************************************************
* Helper functions to restore the heap invariant.
***************************************************************************/
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
private void sink(int k) {
while (2*k <= n) {
int j = 2*k;
if (j < n && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
/***************************************************************************
* Helper functions for compares and swaps.
***************************************************************************/
private boolean less(int i, int j) {
if (comparator == null) {
return ((Comparable) pq[i]).compareTo(pq[j]) < 0;
}
else {
return comparator.compare(pq[i], pq[j]) < 0;
}
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
// is pq[1..N] a max heap?
private boolean isMaxHeap() {
return isMaxHeap(1);
}
// is subtree of pq[1..n] rooted at k a max heap?
private boolean isMaxHeap(int k) {
if (k > n) return true;
int left = 2*k;
int right = 2*k + 1;
if (left <= n && less(k, left)) return false;
if (right <= n && less(k, right)) return false;
return isMaxHeap(left) && isMaxHeap(right);
}
/**
* Returns an iterator that iterates over the keys on this priority queue
* in descending order.
* The iterator doesn't implement {@code remove()} since it's optional.
*
* @return an iterator that iterates over the keys in descending order
*/
public Iterator iterator() {
return new HeapIterator();
}
private class HeapIterator implements Iterator {
// create a new pq
private MaxPQ copy;
// add all items to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
if (comparator == null) copy = new MaxPQ(size());
else copy = new MaxPQ(size(), comparator);
for (int i = 1; i <= n; i++)
copy.insert(pq[i]);
}
public boolean hasNext() { return !copy.isEmpty(); }
public void remove() { throw new UnsupportedOperationException(); }
public Key next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMax();
}
}
}
3.2 小顶堆
public class MinPQ implements Iterable {
private Key[] pq; // store items at indices 1 to n
private int n; // number of items on priority queue
private Comparator comparator; // optional comparator
/**
* Initializes an empty priority queue with the given initial capacity.
*
* @param initCapacity the initial capacity of this priority queue
*/
public MinPQ(int initCapacity) {
pq = (Key[]) new Object[initCapacity + 1];
n = 0;
}
/**
* Initializes an empty priority queue.
*/
public MinPQ() {
this(1);
}
/**
* Initializes an empty priority queue with the given initial capacity,
* using the given comparator.
*
* @param initCapacity the initial capacity of this priority queue
* @param comparator the order in which to compare the keys
*/
public MinPQ(int initCapacity, Comparator comparator) {
this.comparator = comparator;
pq = (Key[]) new Object[initCapacity + 1];
n = 0;
}
/**
* Initializes an empty priority queue using the given comparator.
*
* @param comparator the order in which to compare the keys
*/
public MinPQ(Comparator comparator) {
this(1, comparator);
}
/**
* Initializes a priority queue from the array of keys.
*
* Takes time proportional to the number of keys, using sink-based heap construction.
*
* @param keys the array of keys
*/
public MinPQ(Key[] keys) {
n = keys.length;
pq = (Key[]) new Object[keys.length + 1];
for (int i = 0; i < n; i++)
pq[i+1] = keys[i];
for (int k = n/2; k >= 1; k--)
sink(k);
assert isMinHeap();
}
/**
* Returns true if this priority queue is empty.
*
* @return {@code true} if this priority queue is empty;
* {@code false} otherwise
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Returns the number of keys on this priority queue.
*
* @return the number of keys on this priority queue
*/
public int size() {
return n;
}
/**
* Returns a smallest key on this priority queue.
*
* @return a smallest key on this priority queue
* @throws NoSuchElementException if this priority queue is empty
*/
public Key min() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
// helper function to double the size of the heap array
private void resize(int capacity) {
assert capacity > n;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= n; i++) {
temp[i] = pq[i];
}
pq = temp;
}
/**
* Adds a new key to this priority queue.
*
* @param x the key to add to this priority queue
*/
public void insert(Key x) {
// double size of array if necessary
if (n == pq.length - 1) resize(2 * pq.length);
// add x, and percolate it up to maintain heap invariant
pq[++n] = x;
swim(n);
assert isMinHeap();
}
/**
* Removes and returns a smallest key on this priority queue.
*
* @return a smallest key on this priority queue
* @throws NoSuchElementException if this priority queue is empty
*/
public Key delMin() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
Key min = pq[1];
exch(1, n--);
sink(1);
pq[n+1] = null; // to avoid loiterig and help with garbage collection
if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
assert isMinHeap();
return min;
}
/***************************************************************************
* Helper functions to restore the heap invariant.
***************************************************************************/
private void swim(int k) {
while (k > 1 && greater(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
private void sink(int k) {
while (2*k <= n) {
int j = 2*k;
if (j < n && greater(j, j+1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
/***************************************************************************
* Helper functions for compares and swaps.
***************************************************************************/
private boolean greater(int i, int j) {
if (comparator == null) {
return ((Comparable) pq[i]).compareTo(pq[j]) > 0;
}
else {
return comparator.compare(pq[i], pq[j]) > 0;
}
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
// is pq[1..N] a min heap?
private boolean isMinHeap() {
return isMinHeap(1);
}
// is subtree of pq[1..n] rooted at k a min heap?
private boolean isMinHeap(int k) {
if (k > n) return true;
int left = 2*k;
int right = 2*k + 1;
if (left <= n && greater(k, left)) return false;
if (right <= n && greater(k, right)) return false;
return isMinHeap(left) && isMinHeap(right);
}
/**
* Returns an iterator that iterates over the keys on this priority queue
* in ascending order.
*
* The iterator doesn't implement {@code remove()} since it's optional.
*
* @return an iterator that iterates over the keys in ascending order
*/
public Iterator iterator() {
return new HeapIterator();
}
private class HeapIterator implements Iterator {
// create a new pq
private MinPQ copy;
// add all items to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
if (comparator == null) copy = new MinPQ(size());
else copy = new MinPQ(size(), comparator);
for (int i = 1; i <= n; i++)
copy.insert(pq[i]);
}
public boolean hasNext() { return !copy.isEmpty(); }
public void remove() { throw new UnsupportedOperationException(); }
public Key next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMin();
}
}
}
四、性能分析
- 时间复杂度
插入操作:O(lgN)
删除操作:O(lgN)
建堆:O(NlgN) - 空间复杂度
O(N)