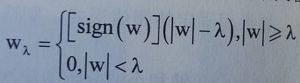小波图像去噪及matlab实例
图像去噪
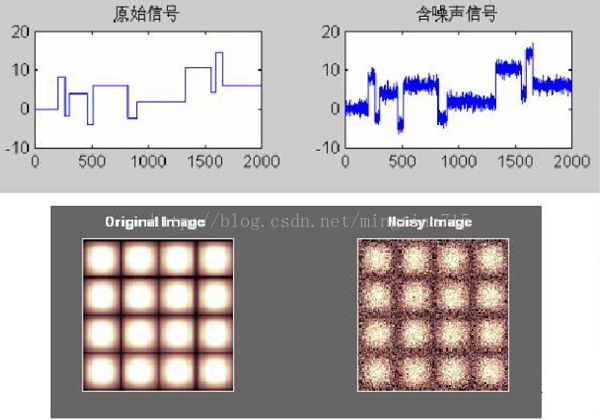
图像去噪是信号处理的一个经典问题,传统的去噪方法多采用平均或线性方法进行,常用的是维纳滤波,但是去噪效果不太好(
维纳滤波在图像复原中的作用
)。
小波去噪
随着小波理论的日益完善,其以自身良好的时频特性在图像去噪领域受到越来越多的关注,开辟了用非线性方法去噪的先河。具体来说,小波能够去噪主要得益于小波变换有如下特点:
(1)低熵性。小波系数的稀疏分布,使图像变换后的熵降低。
意思是对信号(即图像)进行分解后,有更多小波基系数趋于0(噪声),而信号主要部分多集中于某些小波基,采用阈值去噪可以更好的保留原始信号。
(2)多分辨率特性。由于采用了多分辨方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等(例如0-1突变是傅里叶变化无法合理表示的),可以在不同分辨率下根据信号和噪声的分布来消除噪声。
(3)去相关性。小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪。
(4)基函数选择灵活。小波变换可灵活选择基函数,也可根据信号特点和去噪要求选择多带小波和小波包等(小波包对高频信号再次分解,可提高时频分辨率),对不同场合,选择不同小波基函数。
根据基于小波系数处理方式的不同,常见去噪方法可分为三类:
(1)基于小波变换模极大值去噪(信号与噪声模极大值在小波变换下会呈现不同变化趋势)
(2)基于相邻尺度小波系数相关性去噪(噪声在小波变换的各尺度间无明显相关性,信号则相反)
(3)基于小波变换阈值去噪
小波阈值去噪是一种简单而实用的方法,应用广泛,因此重点介绍。
阈值函数选择
阈值处理函数分为软阈值和硬阈值,设w是小波系数的大小,wλ是施加阈值后小波系数大小,λ为阈值。
(1)硬阈值
当小波系数的绝对值小于给定阈值时,令其为0,而大于阈值时,保持其不变,即:
(2)软阈值
当小波系数的绝对值小于给定阈值时,令其为0,大于阈值时,令其都减去阈值,即:
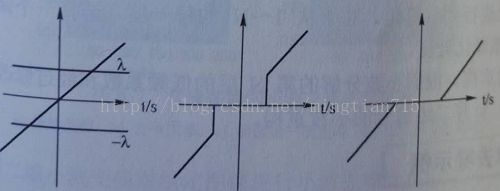
如下图,分别是原始信号,硬阈值处理结果,软阈值处理结果。硬阈值函数在|w| = λ处是不连续的,容易造成去噪后图像在奇异点附近出现明显的伪吉布斯现象。
阈值大小的选取
阈值的选择是离散小波去噪中最关键的一部。在去噪过程中,小波阈值λ起到了决定性作用:如果阈值太小,则施加阈值后的小波系数将包含过多的噪声分量,达不到去噪的效果;反之,阈值太大,则去除了有用的成分,造成失真。小波阈值估计方法很多,这里暂不介绍。
小波去噪实现步骤
(1)二维信号的小波分解。选择一个小波和小波分解的层次N,然后计算信号s到第N层的分解。
(2)对高频系数进行阈值量化。对于从1~N的每一层,选择一个阈值,并对这一层的高频系数进行软阈值量化处理。
(3)二维小波重构。根据小波分解的第N层的低频系数和经过修改的从第一层到第N的各层高频系数,计算二维信号的小波重构
Matlab函数介绍
(1)wavedec2函数
该函数用于对多尺度二维小波进行分解,其常用调用格式:
[C,S] = wavedec2(X,N,'wname'):用小波函数wname对信号X在尺度N上的二维分解,N是严格正整数。
(2)wrcoef2函数
该函数用于对二维小波系数进行单支重构,其调用格式:
X = wrcoef2('type',C,S,'wname',N):用指定的小波函数wname进行N尺度重构。当type = 'a'时,仅对信号的低频部分进行重构,此时N可以为0;当type = 'h'(或'v'/'d')时,对信号(水平、垂直、对角)的高频进行重构,N为严格正整数。
(3)wthcoef2函数
该函数用于对二维信号的小波系数阈值进行处理,常用调用格式:
NC = wthcoef2('type',C,S,N,T,SORH):返回经过小波分解结构[C,S]进行处理后的新的小波分解向量NC,[NC,S]即构成一个新的小波分解结构。N是一个包含高频尺度的向量,T是相应的阈值,且N和T长度须相等。返回'type'(水平、垂直、对角线)方向的小波分解向量NC。参数SORH用来对阈值方式进行选择,当SORH = 's'时,为软阈值,当SORH = 'h'时,为硬阈值。
小波去噪Matlab实例
clear all;
load facets;
subplot(2,2,1);image(X);
colormap(map);
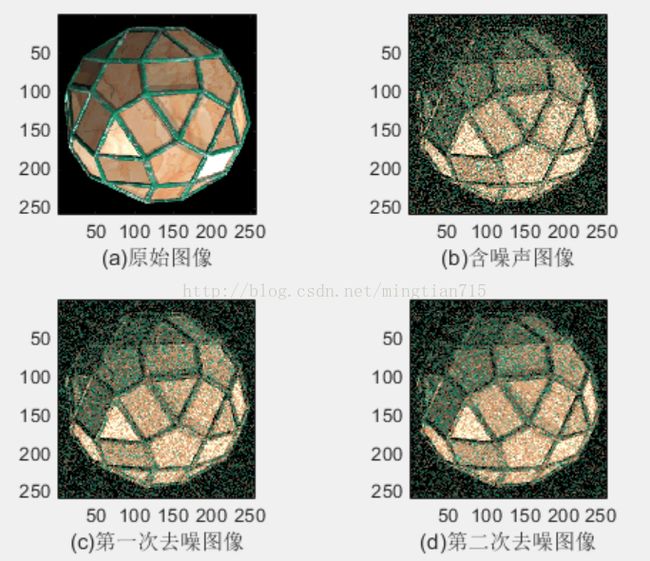
xlabel('(a)原始图像');
axis square
%产生含噪声图像
init = 2055615866;
randn('seed',init);
x = X + 50*randn(size(X));
subplot(2,2,2);image(x);
colormap(map);
xlabel('(b)含噪声图像');
axis square
%下面进行图像的去噪处理
%用小波函数coif3对x进行2层小波分解
[c,s] = wavedec2(x,2,'coif3');
%提取小波分解中第一层的低频图像,即实现了低通滤波去噪
%设置尺度向量
n = [1,2];
%设置阈值向量p
p = [10.12,23.28];
%对三个方向高频系数进行阈值处理
nc = wthcoef2('h',c,s,n,p,'s');
nc = wthcoef2('v',nc,s,n,p,'s');
nc = wthcoef2('d',nc,s,n,p,'s');
%对新的小波分解结构[c,s]进行重构
x1 = waverec2(nc,s,'coif3');
subplot(2,2,3);image(x1);
colormap(map);
xlabel('(c)第一次去噪图像');
axis square
%对nc再次进行滤波去噪
xx = wthcoef2('v',nc,s,n,p,'s');
x2 = waverec2(xx,s,'coif3');
subplot(2,2,4);image(x2);
colormap(map);
xlabel('(d)第二次去噪图像');
axis square
由于例子简单,处理效果一般,但可以明显地看出高频噪声得到了抑制