图像滤波函数imfilter函数的应用及其扩展
一)认识imfilter函数
imfilter函数叫做实现线性空间滤波函数,主要功能可以实现多维数组的滤波,在图像领域就是对图像进行滤波。
滤波是一个统一的概念,在图像领域,图像的去除噪声点,图像提取边缘,图像平滑、模糊、增强等等都可以看成滤波。
用法:B = imfilter(A,H)
B = imfilter(A,H,option1,option2,…)
或写作 :
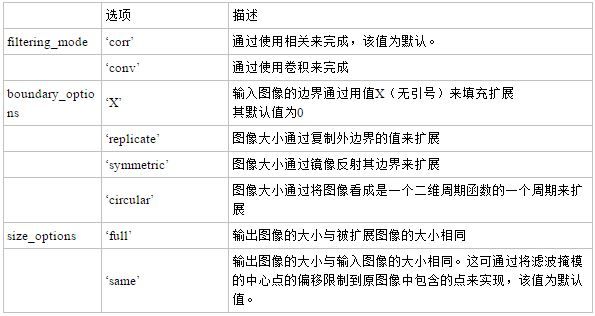
B = imfilter(f, w, filtering_mode, boundary_options, size_options);
(更详细的在matlab环境下help查询imfilter函数)这里贴出来help的文件如下:
二)认识模板H
可以说imfilter函数的精髓就是对于模板H的构造,H的不同决定了你的实现效果不同,那么什么是模板呢?举个例子,假如现在要提取图像的噪声点,我们知道,既然是噪声点,那么噪声点的像素值与其周围的点的像素值都应该相差很远才对,这里选取噪声点的上下左右四个方向,每个方向上用噪声点的值减去对应方向的值,将这四个差的绝对值相加起来,如果这个值越大,是不是说明这个点越是噪声点了,那么上述的这个过程可以用一个模板来计算,这个模板就是:
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
用这个模板去对图像滤波就可以得到噪声(当然也可以得到边缘,因为边缘也符合这个特性吧),比如下图所示:

该图就是经过模板H = [0 -1 0;-1 4 -1;0 -1 0]滤波而来的,相应的matlab代码就是imfilter(I,H);
其实这个滤波函数的操作方式很简单,对于一个图像的一个像素点的操作,首先看看模板大小,比如3*3,然后提取出这个像素点附近的3*3领域的9个像素点,将这9个像素点依次对应的与模板中的数字相乘,在把乘的所有值相加(很显然就会出现正负了,不一定都是正值),把这个和作为该像素点滤波后的值,那么图像中每个像素点都进行这个操作后,就得到一副与原始图像大小相同的滤波图像了,比如上面这幅图。
由上可知模板对于图像滤波功能的重要性。像上述的一个模板,这个模板也被称为拉普拉斯模板,类似的还有边缘检测算子,canny算子,sobel算子等等,相关介绍:
http://www.kongzhi.net/cases/caseview.php?id=2368
比如说边缘检测竖线的算子就可以表示为H = [-1 2 -1;-1 2 -1;-1 2 -1],得到的结果就如下所示:

三)一个问题
到这可能有人思考到,既然这个算子对像素点的处理是该像素点的附近像素点的一个加权和,那么对于一副图像的边缘怎么办?还是说3*3模板,现在要对最左边、最上边的那个像素点处理怎么办?它的上边、左边没有像素点了呀,这就涉及到扩充边缘了,也就是imfilter函数里面的boundary_options参数,matlab的扩充方式有如上的3中方式,复制边界、镜像边界、按周期扩充,像复制边界,就是讲边界点复制到没有的边界,加入100*100的图像,使用3*3的模板,那么复制边界后的图像就是102*102的图像了,这就引除了imfilter的第三个参数size_options,这个参数决定输出的图像是与原图像大小的呢还是扩充边界的呢,一般情况下,默认输出原图像大小的,也就是102*102的图像在输出时又会去掉所加的边界,重新变成100*100的图像。 当然,关于边界的处理问题,也可以自己编程去扩充,生成一个大一点的图像去储存起来,然后把边界点复制过去。四)关于imfilter的应用扩展
对于imfilter函数的应用远不止于滤波,其实对于H的构造可以快速实现很多复杂的操作,尤其是对于整幅图像来说(并且会涉及到边界问题的时候)。
一个简单的例子,假设现在一副图像,我们要提取图像中每个像素点的特征值,这个特征值包括四个特征(灰度值、像素点横向梯度、像素点纵向梯度、像素点的领域内方差),各个特征的计算方式如下所示:
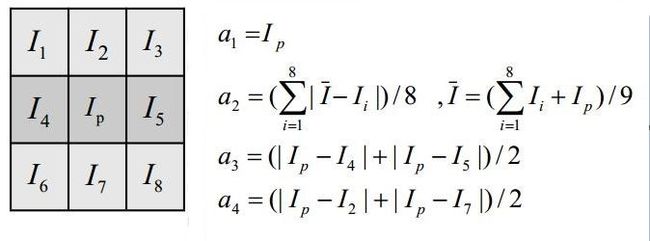
当需要求所有像素点的这四个特征的时候怎么办?一种方法直接按照公式给的求解,编程实现这四个特征也很简单,然后对于每一个像素点来一个for循环。这样带来两个问题:(1)你的边界点怎么办?边界点的上下左右总有个方向没有像素点吧,这个时候你必须去扩充边界才能继续。(2)我们知道for循环耗时耗力,对于matlab这个矩阵实验室来说,对矩阵整体操作最好不过了,速度快,最忌讳的就是在matlab中去大量使用for循环,用起来慢死你(某些问题)。
这里我们就采用滤波函数imfilter来分解实现上述四个特征的求解过程,使得计算的速度加快并且简单。特征a1不要说,就是原始图像。最麻烦的特征a2,a2为领域类方差,首先得求解该3*3领域内均值,就是该领域内的所有像素点求和再求平均,这就需要均值个模板:
model = 1/9*[1 1 1;1 1 1;1 1 1];
F2_mean = imfilter(img,model,'replicate');边界的扩充方式采用复制的方式,默认生成大小与原图像一样大的。然后是均值与领域内的像素点相减求和再求均值,那么首先得把领域内的像素点都调整到中心点位置,这就需要8个模板了,相应的程序:
model_1 = [-1 0 0;0 0 0;0 0 0];F2_1 = imfilter(img,model_1,'replicate');
model_2 = [0 -1 0;0 0 0;0 0 0];F2_2 = imfilter(img,model_2,'replicate');
model_3 = [0 0 -1;0 0 0;0 0 0];F2_3 = imfilter(img,model_3,'replicate');
model_4 = [0 0 0;-1 0 0;0 0 0];F2_4 = imfilter(img,model_4,'replicate');
model_5 = [0 0 0;0 0 -1;0 0 0];F2_5 = imfilter(img,model_5,'replicate');
model_6 = [0 0 0;0 0 0;-1 0 0];F2_6 = imfilter(img,model_6,'replicate');
model_7 = [0 0 0;0 0 0;0 -1 0];F2_7 = imfilter(img,model_7,'replicate');
model_8 = [0 0 0;0 0 0;0 0 -1];F2_8 = imfilter(img,model_8,'replicate');
F2=0.125*(abs(F2_mean+F2_1)+abs(F2_mean+F2_2)+abs(F2_mean+F2_3)+abs(F2_mean+F2_4)+...
abs(F2_mean+F2_5)+abs(F2_mean+F2_6)+abs(F2_mean+F2_7)+abs(F2_mean+F2_8));得到的F2就是整幅图像的a2特征了,可以看到没有循环,不用自己去设计边界扩充,速度还特别的快。
接着是a3与a4特征,这两个特征也比较简单,如下:
F3 = 0.5*(abs(img + F2_4) + abs(img + F2_5));
F4 = 0.5*(abs(img + F2_2) + abs(img + F2_7));至此,像素点的这四个特征就差不多了,可以看到imfilter函数还是非常强大的,尤其是对于所有像素点的整体操作的时候(而且图像方面一般都是整体操作),不过是通常用的边缘提取、滤波等等原图,对于其他问题,只要能够分解为简单的加和问题,都可以方便的用imfilter来求解。