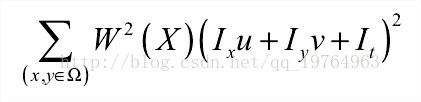Lucas-Kanade光流法
1. 光流的概念
•空间运动物体在观察成像平面上的像素运动的瞬时速度
2. 光流法的原理
•利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系,从而计算出相邻帧之间物体的运动信息,即光流
光流的分类:稠密光流与稀疏光流(Lucus-Kanade算法)
3. L-K光流
Lucas-Kanada最初于1981年提出,该算法假设在一个小的空间邻域内运动矢量保持恒定,使用加权最小二乘法估计光流。由于该算法应用于输入图像的一组点上时比较方便,因此被广泛应用于稀疏光流场。
4. 三个假设
假设一:场景中物体被跟踪的部分亮度保持不变
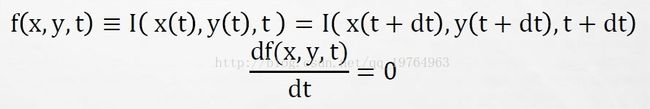
假设二:运动相对于帧率是缓慢、连贯的数学表达指的是在上连续,可导
假设三:相邻的点保持近邻δ邻域内所有像素点的速度(U,V)相等
由假设二,对假设一应用偏微分链式法则,则得到L-K算法核心的数学描述公式:
5. 图像金字塔的引入L-K算法
对于大多数30Hz摄像机,大而不连贯的运动较多,所以LK光流法在实际中的跟踪效果不好,通常一个大的窗口来捕获大的运动,但往往违背运动连贯的假设,故引入图像金字塔。
在图像金字塔的最高层计算光流,用得到的运动估计结果作为下一层金字塔的起始点,重复这个过程直到到达金字塔的最底层。这样将不满足运动假设的可能性降到最小从而实现对更快和更长的运动的跟踪。
6. 计算方法
在一个小的邻域内,我们通过对下式的加权平方和最小化来估计V,
Lucas–Kanade算法:
这个算法是最常见,最流行的。它计算两帧在时间t 到t +δt之间每个每个像素点位置的移动。 由于它是基于图像信号的泰勒级数,这种方法称为差分,这就是对于空间和时间坐标使用偏导数。
图像约束方程可以写为I(x,y,z,t)= I(x + δx,y + δy,z + δz,t + δt)
I(x, y,z, t) 为在(x,y,z)位置的体素。
我们假设移动足够的小,那么对图像约束方程使用泰勒公式,我们可以得到:
![I(x+\delta x,y+\delta y,z+\delta z,t+\delta t) = I(x,y,z,t) + \frac{\partial I}{\partial x}\delta x+\frac{\partial I}{\partial y}\delta y+\frac{\partial I}{\partial z}\delta z+\frac{\partial I}{\partial t}\delta t+H.O.T.]()
H.O.T. 指更高阶,在移动足够小的情况下可以忽略。从这个方程中我们可以得到:
或者
我们得到:
Vx,Vy,Vz分别是I(x,y,z,t)的光流向量中x,y,z的组成。 ,
,
和
则是图像在(x,y,z,t)这一点向相应方向的差分。
所以
IxVx + IyVy + IzVz= − It。
写做:
这个方程有三个未知量,尚不能被解决,这也就是所谓光流算法的光圈问题。那么要找到光流向量则需要另一套解决的方案。而Lucas-Kanade算法是一个非迭代的算法:
假设流(Vx,Vy,Vz)在一个大小为m*m*m(m>1)的小窗中是一个常数,那么从像素1...n, n = m3中可以得到下列一组方程:
三个未知数但是有多于三个的方程,这个方程组自然是个超定方程,也就是说方程组内有冗余,方程组可以表示为:
记作:
为了解决这个超定问题,我们采用最小二乘法:
or
得到:
其中的求和是从1到n。
这也就是说寻找光流可以通过在四维上图像导数的分别累加得出。我们还需要一个权重函数W(i, j,k), 来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的,
这个算法的不足在于它不能产生一个密度很高的流向量,例如在运动的边缘和黑大的同质区域中的微小移动方面流信息会很快的褪去。它的优点在于有噪声存在的鲁棒性还是可以的。
补充:opencv里实现的看上去蛮复杂,现在还不是太明白。其中LK经典算法也是迭代法,是由高斯迭代法解线性方程组进行迭代的。
参考文献:Lucas B and Kanade T. An Iterative Image RegistrationTechnique with an Application to Stereo Vision. Proc. Of 7th InternationalJoint Conference on Artificial Intelligence (IJCAI), pp.674-679.是81年发表的。
opencv中实现的是84年发表的算法,
参考文献:Bruce D. Lucas,"Generalized Image Matching by the Method of Differences," doctoraldissertation, tech. report , Robotics Institute, Carnegie Mellon University,July, 1984
这篇论文是收费的,一直都没下到还。