JavaScript数据结构之 —— 10排序算法和搜索算法

排序算法

开始排序算法之前，我们先创建一个数组来表示待排序和搜索的数据结构：

function ArrayList(){
	var array = []; //存储
	this.insert = function(item){ //添加元素
		array.push(item);
	};
	this.toString= function(){ //方便查看数组输出结果
		return array.join();
	};
}

网上找的一张图:

冒泡排序

人们开始学习排序算法时，通常都先学冒泡算法，因为它在所有排序算法中最简单。然而，从运行时间的角度来看，冒泡排序是最差的一个，接下来你会知晓原因。

冒泡排序比较任何两个相邻的项，如果第一个比第二个大，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样，冒泡排序因此得名。
实现冒泡排序：

this.bubbleSort = function(){
	var length = array.length; // 存储数组长度
	for (var i=0; i<length; i++){ // 外循环：每一项进行一轮排序
		for (var j=0; j<length-1; j++ ){ //从第一项到倒数第二项
			if (array[j] > array[j+1]){ //相邻项比较，前项大就交换位置
				swap(j, j+1); 
			}
		}
	}
};

// 声明一个交换函数
var swap = function(index1, index2){
	var aux = array[index1]; // 用一个中间值来存储某一交换项的值
	array[index1] = array[index2];
	array[index2] = aux;
};

改进后的冒泡排序：

this.modifiedBubbleSort = function(){
	var length = array.length;
	for (var i=0; i<length; i++){
		for (var j=0; j<length-1-i; j++ ){ 
		// 因为每一轮排序，都会将一个最大的放到最后
		// 如果从内循环减去外循环中已跑过的轮数
		// 就可以避免内循环中所有不必要的比较
			if (array[j] > array[j+1]){
				swap(j, j+1);
			}
		}
	}
};

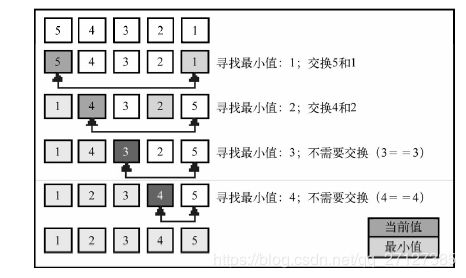
改进后的排序效果如下图，注意已经在正确位置上的数字没有被比较。即便我们做了这个小改变，改进了一下冒泡排序算法，但我们还是不推荐该算法，它的复杂度是O(n2)。：

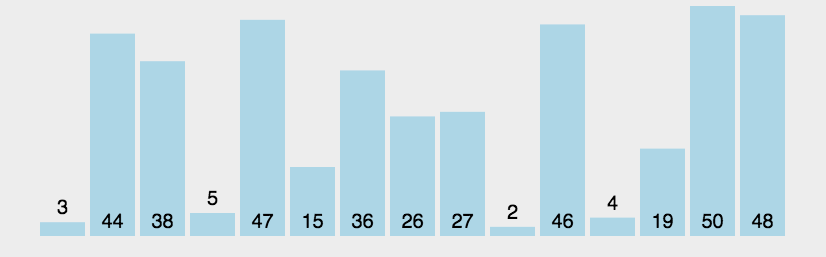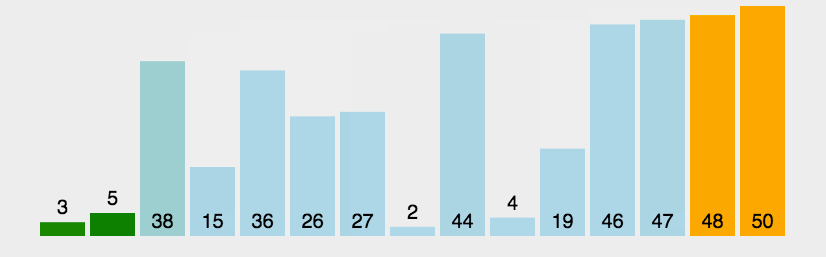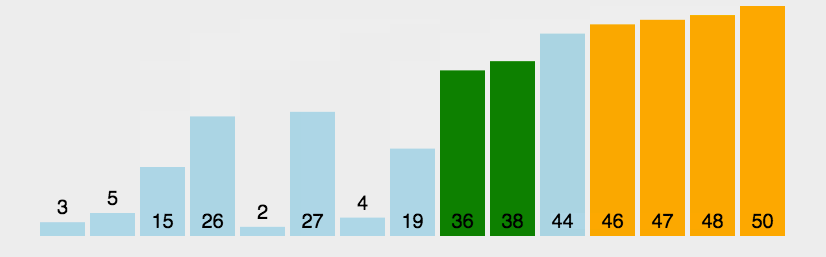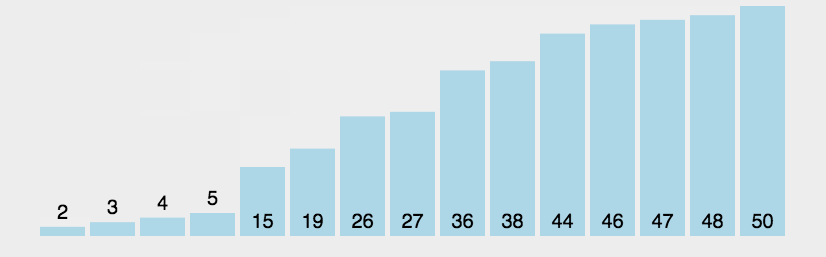
选择排序

选择排序大致的思路是找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。

this.selectionSort = function(){
	var length = array.length, 
	indexMin;
	for (var i=0; i<length-1; i++){ // 外层循环比较次数
		indexMin = i; //存储本轮最小值
		for (var j=i; j<length; j++){ // 获取剩下元素的最小值
			if(array[indexMin]>array[j]){ 
			// 比较并保证 indexMin 为最小值的下标
				indexMin = j; 
			}
		}	
		if (i !== indexMin){ // 本轮第一个，存储为本轮最小值
			swap(i, indexMin);
		}
	}
};

选择排序看起来比冒泡简单些，不过同样也是一个复杂度为O(n2)的算法。和冒泡排序一样，它包含有嵌套的两个循环，这导致了二次方的复杂度。

插入排序

插入排序每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序了，接着，它和第二项进行比较，第二项是应该待在原位还是插到第一项之前呢？这样，头两项就已正确排序，接着和第三项比较（它是该插入到第一、第二还是第三的位置呢？），以此类推。

this.insertionSort = function(){
	var length = array.length, 
	j, temp;
	for (var i=1; i<length; i++){ // 外层循环比较第 i 项
		j = i; 
		temp = array[i]; // 存储临时变量
		while (j>0 && array[j-1] > temp){ 
		// 前一位如果大于当前位，就把前一位的值放到当前位置
			array[j] = array[j-1]; 
			j--;
		}
		// 最后把临时变量放进比较结束后最前面的位置
		array[j] = temp; 
	}
};

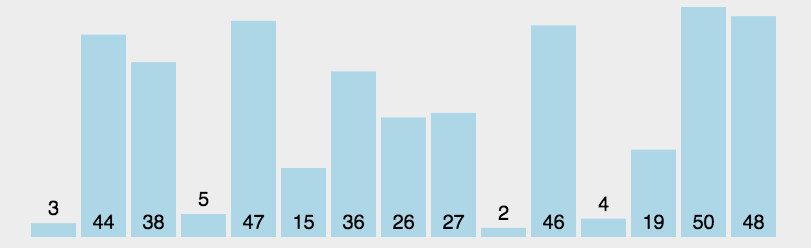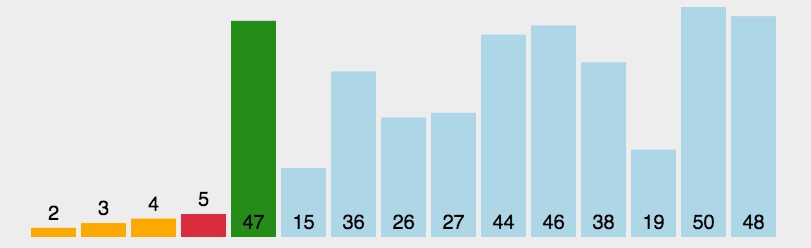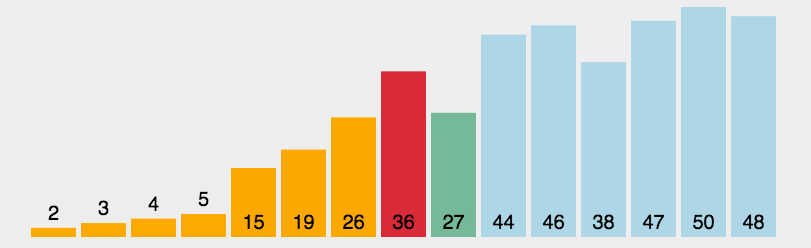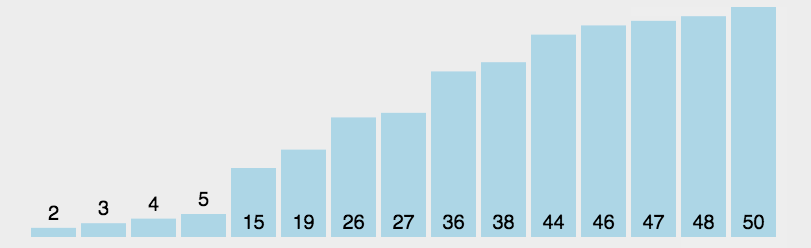
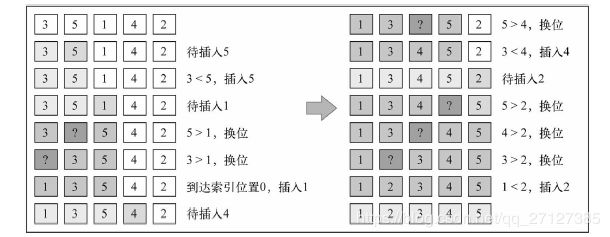
看个图以便理解：
这些值将被插入排序算法按照下面形容
的步骤进行排序。
(1) 3已被排序，所以我们从数组第二个值5开始。3比5小，所以5待在原位（数组的第二位）。3和5排序完毕。
(2) 下一个待排序和插到正确位置上去的值是1（目前在数组的第三位）。5比1大，所以5被移至第三位去了。我们得分析1是否应该被插入到第二位——1比3大吗？不，所以3被移到第二位去了。接着，我们得证明1应该插入到数组的第一位上。因为0是第一个位置且没有负数位，所以1必须被插入到第一位。1、3、5三个数字已经排序。。。以此类推。

排序小型数组时，此算法比选择排序和冒泡排序性能要好。

归并排序

归并排序是第一个可以被实际使用的排序算法。前三个排序算法性能不好，但归并排序性能不错，其复杂度为O(nlogn)。

其思想是将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

this.mergeSort = function(){
	array = mergeSortRec(array);
};

var mergeSortRec = function(array){
	var length = array.length;
	if(length === 1) { 
	// 由于算法是递归的，我们需要一个停止条件
	// 在这里此条件是判断数组的长度是否为1
		return array; 
	}
	// 如果数组长度比1大，那么我们得将其分成小数组。
	// 为此，首先得找到数组的中间位,
	// 找到后我们将数组分成两个小数组，分别叫作left和right
	var mid = Math.floor(length / 2), 
	left = array.slice(0, mid), 
	right = array.slice(mid, length); 
	return merge(mergeSortRec(left), mergeSortRec(right)); 
};

下面的步骤是调用merge函数负责合并和排序小数组来产生大数组，直到回到原始数组并已排序完成。为了不断将原始数组分成小数组，我们得再次对left数组和right数组
递归调用mergeSortRec，并同时作为参数传递给merge函数。

var merge = function(left, right){
	var result = [], // 存储结果的数组
	il = 0,
	ir = 0;
	while(il < left.length && ir < right.length) { 
	// 左右两个数组都有值存在，就挨个比较左右两个数组的元素
	// 取出最小值，push 到本轮数组中
	// 直到有一个数组的所有元素都被取出
		if(left[il] < right[ir]) {
			result.push(left[il++]); 
		} else{
			result.push(right[ir++]); 
		}
	}
	// 如果左侧数组剩余元素，就取出它剩下的元素，放到新数组中
	while (il < left.length){ 
		result.push(left[il++]);
	}
	while (ir < right.length){ 
		result.push(right[ir++]);
	}
	return result; // 返回排序后的新数组
};

merge函数接受两个数组作为参数，并将它们归并至一个大数组。排序发生在归并过程中。
首先，需要声明归并过程要创建的新数组以及用来迭代两个数组（left和right数组）所需的两个变量。迭代两个数组的过程中，我们比较来自left数组的项是否比来自right
数组的项小。如果是，将该项从left数组添加至归并结果数组，并递增迭代数组的控制变量；否则，从right数组添加项并递增相应的迭代数组的控制变量。接下来，将left
数组或者right数组所有剩余的项添加到归并数组中。最后，将归并数组作为结果返回。

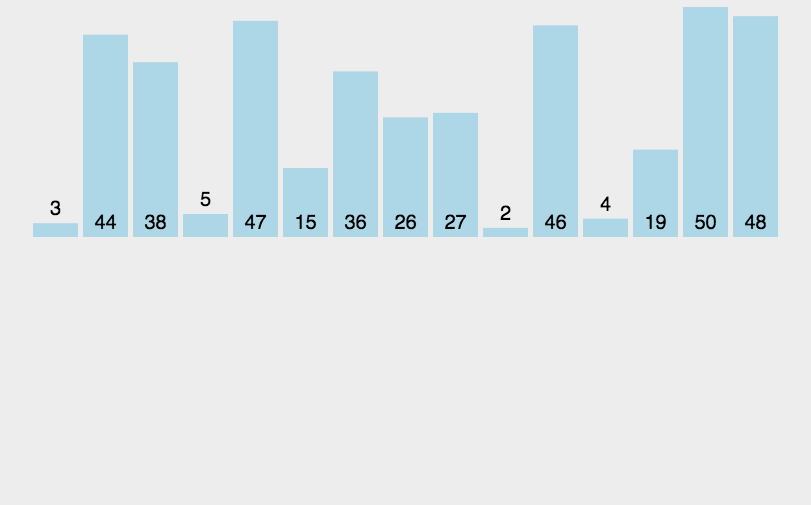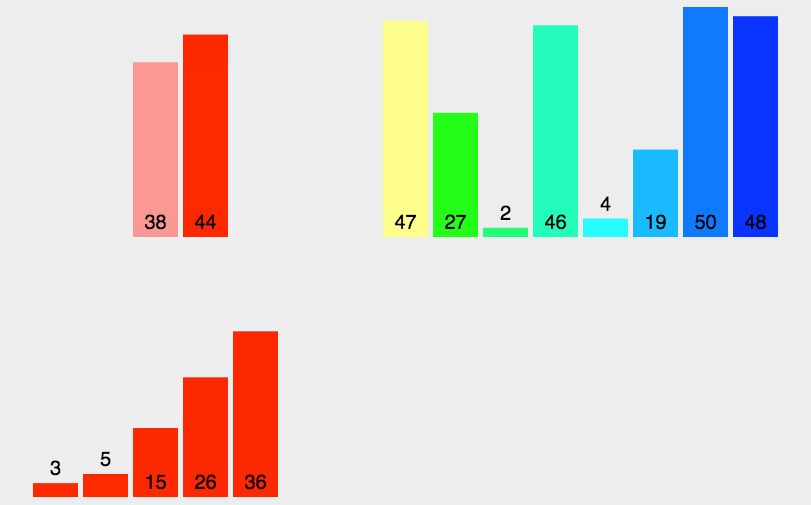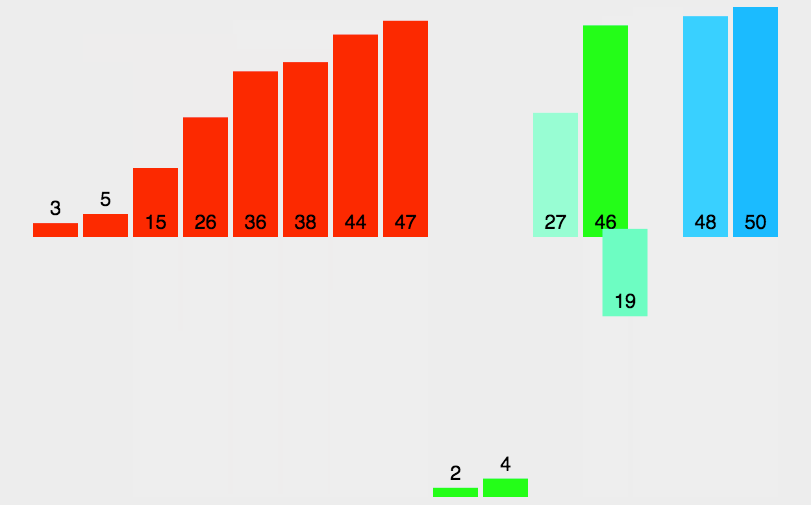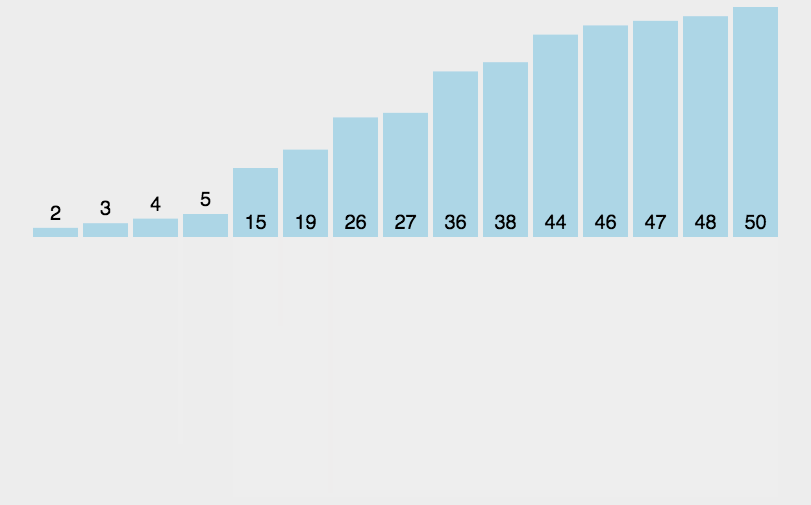
算法首先将原始数组分割直至只有一个元素的子数组，然后开始归并。归并过程也会完成排序，直至原始数组完全合并并完成排序。

快速排序

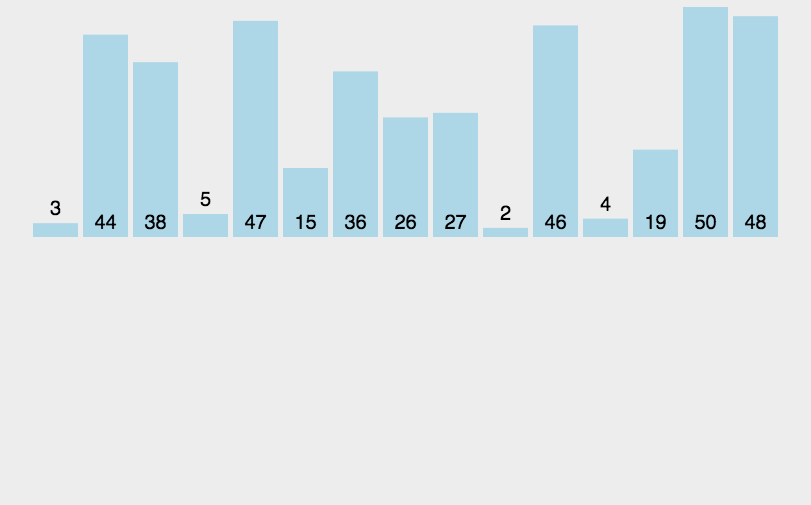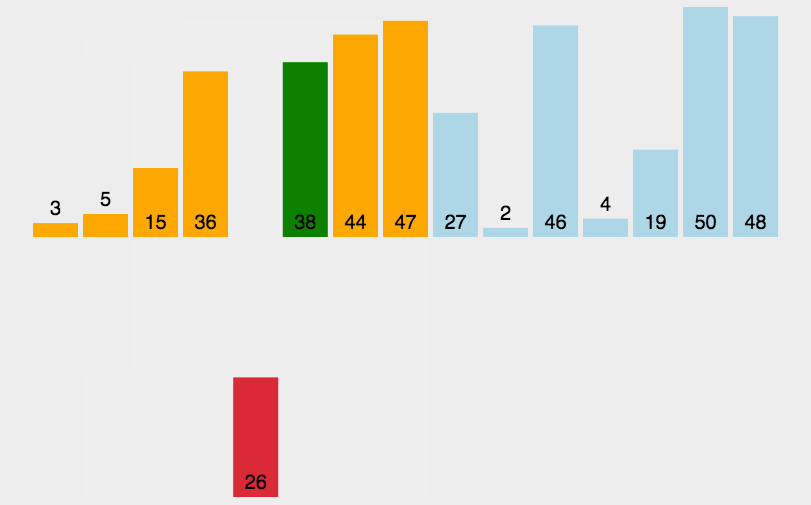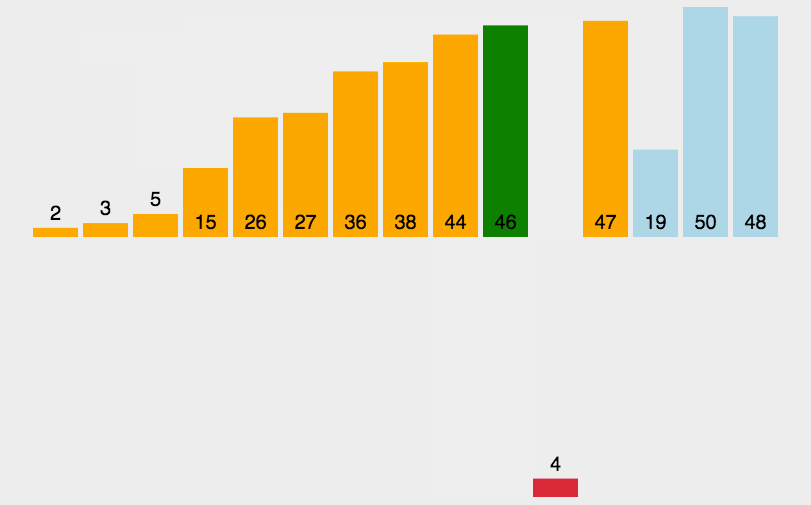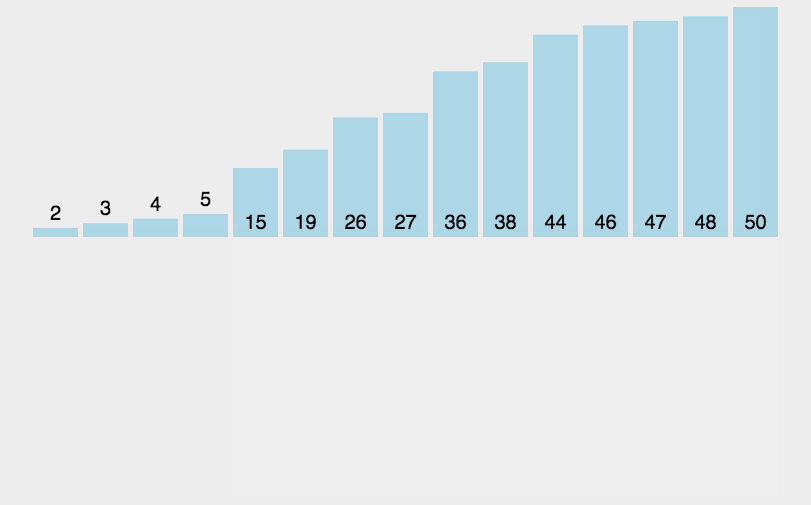
这个算法首先要在列表中选择一个元素作为基准值（pivot）。数据排序围绕基准值进行，
将列表中小于基准值的元素移到数组的前面，将大于基准值的元素移到数组的后面。
实现过程如下：
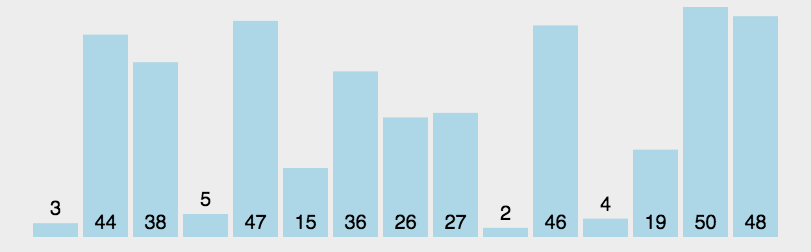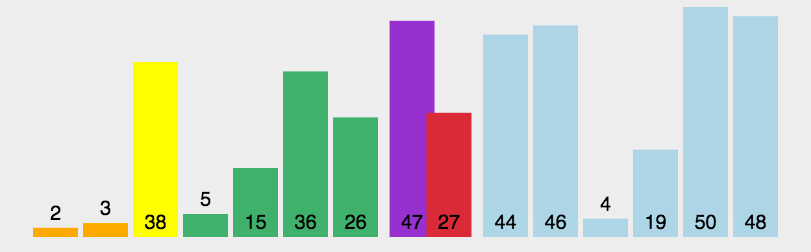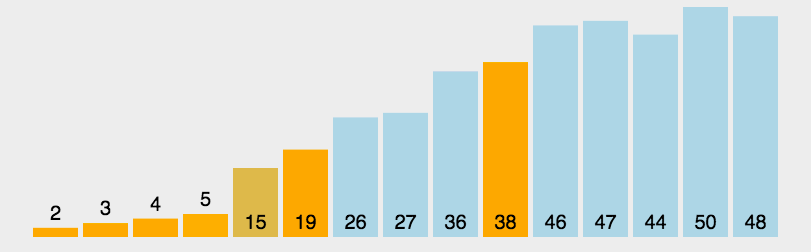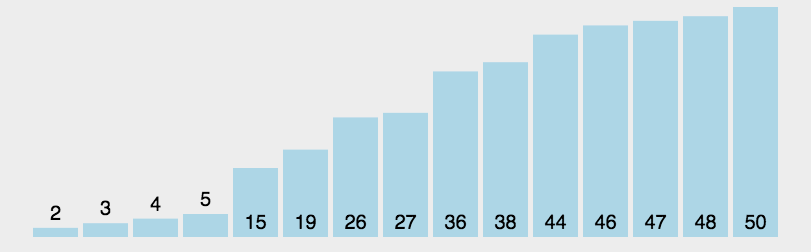
(1) 选择一个基准元素，将列表分隔成两个子序列；
(2) 对列表重新排序，将所有小于基准值的元素放在基准值的前面，所有大于基准值的元
素放在基准值的后面；
(3) 分别对较小元素的子序列和较大元素的子序列重复步骤 1 和 2。

function qSort(list) {
	if (list.length == 0 || list.length == 1) {
	// 如果数组长度为零或一，就不需要排序，直接返回
		return list;
	}
	// 创建左右数组用来存数据
	var left = [],right = [];
	// 设置基准值
	var pivot = list[0]; 
	for (var i = 1; i < list.length; i++) {
		if (list[i] < pivot) {
			left.push(list[i]);
		} else {
			right.push(list[i]);
		}
	}
	// 左右两个数组分别调用这个函数
	// 然后把所有的值组合成一个数组
	// 排序完成
	return qSort(left).concat(pivot, qSort(right));
}

测试排序效果：

for (var i = 0; i < 10; ++i) {
	a[i] = Math.floor((Math.random()*100)+1);
}
console.log('排序前：',a);
console.log('排序后：',qSort(a));

搜索算法

在列表中查找数据有两种方式：顺序查找和二分查找。顺序查找适用于元素随机排列的列表；二分查找适用于元素已排序的列表。二分查找效率更高，但是你必须在进行查找之前花费额外的时间将列表中的元素排序。

顺序搜索

顺序查找，有时也被称为线性查找。从列表的第一个元素开始循环，然后逐个与要查找的数据进行比较。如果匹配到了，则结束查找。如果到了列表的结尾也没有匹配到，那么这个数据就不存在于这个列表中。

function seqSearch(arr, data) {
	for (var i = 0; i < arr.length; ++i) {
		if (arr[i] == data) {
			return i;
		}
	}
	return false;
}

查找最小值
第一个元素作为最小值，遍历过程中，遇到更小值就替换它

function findMin(arr) {
	var min = arr[0];
	for (var i = 1; i < arr.length; ++i) {
		if (arr[i] < min) {
			min = arr[i];
		}
	}
	return min;
}

二分查找

(1) 选择数组的中间值。
(2) 如果选中值是待搜索值，那么算法执行完毕（值找到了）。
(3) 如果待搜索值比选中值要小，则返回步骤1并在选中值左边的子数组中寻找。
(4) 如果待搜索值比选中值要大，则返回步骤1并在选种值右边的子数组中寻找。

function binSearch(arr, data) {
	this.quickSort(); // 开始之前先排序
	
	// 边界指针
	var low = 0, high = array.length - 1, 
	mid, element;

	// 边界重合了都没查到就返回 -1
	while (low <= high){ 
		// 取中间值作为比较值和分割点
		mid = Math.floor((low + high) / 2); 
		element = array[mid]; 
		if (element < item) { 
			low = mid + 1; // 更新下边界
		} else if (element > item) { 
			high = mid - 1; // 更新上边界
		} else {
			return mid; // 不大不小正正好
		}
	}
	return -1; //{12}
}