Forward and Backward Information Retention for Accurate Binary Neural Networks
Forward and Backward Information Retention for Accurate Binary Neural Networks
文章目录
- Forward and Backward Information Retention for Accurate Binary Neural Networks
- Introduction
- Preliminaries
- Information Retention Network
- Libra Parameter Binarization in Forward Propagation
- Error Decay Estimator in Backward Propagation
- Experiments
- Summary
文章链接
代码链接
Introduction
作者认为，二值网络的精度损失主要在于limited representation ability and discreteness of binarization，这就导致了在前向和反向过程中巨大的信息损失。同时，由于在前向过程中，权重和激活值被限制在两个值，因此表达能力大大下降，反向过程中，直接的STE求导方法会导致梯度不准确的问题。针对以上问题，之前的一些做法经常忽略离开训练的不同stage带来的差异，训练的早期阶段，网络需要一个很强的参数更新能力，在后期阶段，准确的梯度方向就更为重要(梯度匹配)。
针对以上的问题，作者从信息流的角度出发，提出了Information Retention Network (IR-Net)，主要解决上面说的前传和反传中出现的两个问题。
- 在前向过程中引入了Libra Parameter Binarization (Libra-PB)，通过最大化量化参数的熵、最小化量化误差，来减小前向过程中信息的损失，从而保证特征的多样性
- 在反向过程中，引入Error Decay Estimator (EDE)来计算梯度，让梯度在训练的不同阶段都能够计算地更为准确
Preliminaries
一般激活值的计算方法为 z = w T a z = w^{T}a z=wTa式中 w ∈ R n w \in \mathbb{R}^{n} w∈Rn表示网络的权重， a ∈ R n a \in \mathbb{R}^{n} a∈Rn表示网络某一层的输入。对于二值网络，则是 Q x ( x ) = a B x Q_{x}(\texttt{x})=a\texttt{B}_{\texttt{x}} Qx(x)=aBx其中， x \texttt{x} x表示浮点参数，包括浮点的权重 w w w和激活值 a a a， B x ∈ { − 1 , + 1 } n \texttt{B}_{\texttt{x}}\in \left \{ -1,+1 \right \}^{n} Bx∈{−1,+1}n表示二值化的参数，包括二值化的权重 B w \texttt{B}_{\texttt{w}} Bw和 B a \texttt{B}_{\texttt{a}} Ba， a a a表示二值化的尺度因子，包括权重的 a w a_{\texttt{w}} aw和激活值的 a a a_{\texttt{a}} aa，一般地，使用 sign 函数来得到二值化激活值 B x = sign ( x ) = { + 1 , if x ≥ 0 − 1 , otherwise \mathbf{B}_{\mathbf{x}}=\operatorname{sign}(\mathbf{x})=\left\{\begin{array}{ll} +1, & \text { if } \mathbf{x} \geq 0 \\ -1, & \text { otherwise } \end{array}\right. Bx=sign(x)={+1,−1, if x≥0 otherwise 前向的传播过程如下式所示： z = Q w ( w ) ⊤ Q a ( a ) = α w α a ( B w ⊙ B a ) z=Q_{w}(\mathbf{w})^{\top} Q_{a}(\mathbf{a})=\alpha_{\mathrm{w}} \alpha_{\mathrm{a}}\left(\mathbf{B}_{\mathbf{w}} \odot \mathbf{B}_{\mathbf{a}}\right) z=Qw(w)⊤Qa(a)=αwαa(Bw⊙Ba)式中， ⊙ \odot ⊙为XNOR或Bitcount表示的矢量内积，一般的求导方式为STE。
Information Retention Network
Libra Parameter Binarization in Forward Propagation
一般而言，一个最优的quantizer的求解方式如下： min J ( Q x ( x ) ) = ∥ x − Q x ( x ) ∥ 2 \min J\left(Q_{x}(\mathbf{x})\right)=\left\|\mathbf{x}-Q_{x}(\mathbf{x})\right\|^{2} minJ(Qx(x))=∥x−Qx(x)∥2 x \mathbf{x} x表示全精度的参数， Q x ( x ) Q_{x}(\mathbf{x}) Qx(x)表示量化参数， J ( Q x ( x ) ) J\left(Q_{x}(\mathbf{x})\right) J(Qx(x))表示量化误差，但是二值化网络的解空间和全精度网络并不相同，最小化量化误差不一定能得到一个性能优异的二值网络。基于这一点，作者提出了Libra ParameterBinarization (Libra-PB)，把量化误差和信息损失放在一起考虑，进而对网络进行优化。
那么。对于信息的损失，作者到底是怎么衡量的呢？对于一个服从伯努利分布的随机变量 b ∈ { − 1 , + 1 } b \in\{-1,+1\} b∈{−1,+1}，它的分布为： f ( b ) = { p , if b = + 1 1 − p , if b = − 1 f(b)=\left\{\begin{array}{ll} p, & \text { if } b=+1 \\ 1-p, & \text { if } b=-1 \end{array}\right. f(b)={p,1−p, if b=+1 if b=−1其中， p p p表示取 + 1 +1 +1的概率， p ∈ { 0 , + 1 } p \in\{0,+1\} p∈{0,+1}(原文是-1到1，疑似笔误)，二值网络正好可以看成是一个伯努利分布的一个采样，因此，上面的 Q x ( x ) Q_{x}(\mathbf{x}) Qx(x)的熵可以如下的方法计算(就是信息熵的计算方法)： H ( Q x ( x ) ) = H ( B x ) = − p ln ( p ) − ( 1 − p ) ln ( 1 − p ) \mathcal{H}\left(Q_{x}(\mathbf{x})\right)=\mathcal{H}\left(\mathbf{B}_{\mathbf{x}}\right)=-p \ln (p)-(1-p) \ln (1-p) H(Qx(x))=H(Bx)=−pln(p)−(1−p)ln(1−p)由于熵越大，表示混乱程度越大，潜在的表达能力就越高(不太明白的可以看看信息论中“熵”的相关内容)，所以就需要最大化这个熵，即最小化熵的相反数，然后和前面的量化误差结合起来，就有了新的损失函数： min J ( Q x ( x ) ) − λ H ( Q x ( x ) ) \min J\left(Q_{x}(\mathbf{x})\right)-\lambda \mathcal{H}\left(Q_{x}(\mathbf{x})\right) minJ(Qx(x))−λH(Qx(x))在伯努利分布下，当 p = 0.5 p = 0.5 p=0.5时，量化参数的熵取最大值，说明，此时的量化参数是均匀分布的(取正负的概率一半一半)，因此，为了让权重分布有关于0对称的属性，作者先将全精度的权重都减去了其均值，此外，为了训练更加稳定，不受权重数值的影响，将权重归一化。所以作者得到的balanced weight w ^ s t d \hat{\mathbf{w}}_{\mathrm{std}} w^std包括以下两个步骤： w ^ s t d = w ^ σ ( w ^ ) , w ^ = w − w ‾ \hat{\mathbf{w}}_{\mathrm{std}}=\frac{\hat{\mathbf{w}}}{\sigma(\hat{\mathbf{w}})}, \quad \hat{\mathbf{w}}=\mathbf{w}-\overline{\mathbf{w}} w^std=σ(w^)w^,w^=w−w其中， σ ( ⋅ ) \sigma(\cdot) σ(⋅)表示标准差， w ^ s t d \hat{\mathbf{w}}_{\mathrm{std}} w^std有两个比较好的性质，一个是zero-mean，一个是unit-norm。
论文中这一部分剩下的大部分内容，就是在讲它把尺度因子 a a a也量化了，这样可以加速计算，直接用移位操作就行。所以，网络激活值的计算就变成了以下几步： Q w ( w ^ s t d ) = B w ≪ ≫ s = sign ( w ^ s t d ) ≪ ≫ s Q_{w}\left(\hat{\mathbf{w}}_{\mathrm{std}}\right)=\mathbf{B}_{\mathbf{w}} \ll \gg s=\operatorname{sign}\left(\hat{\mathbf{w}}_{\mathrm{std}}\right) \ll \gg s Qw(w^std)=Bw≪≫s=sign(w^std)≪≫s Q a ( a ) = B a = sign ( a ) Q_{a}(\mathbf{a})=\mathbf{B}_{\mathbf{a}}=\operatorname{sign}(\mathbf{a}) Qa(a)=Ba=sign(a) z = ( B w ⊙ B a ) ≪ ≫ s z=\left(\mathbf{B}_{\mathbf{w}} \odot \mathbf{B}_{\mathbf{a}}\right) \ll \gg s z=(Bw⊙Ba)≪≫s其中， s s s就是计算出的移位尺度因子，计算方法如下： s ∗ = round ( log 2 ( ∥ w ^ s t d ∥ 1 / n ) ) s^{*}=\operatorname{round}\left(\log _{2}\left(\left\|\hat{\mathbf{w}}_{\mathrm{std}}\right\|_{1} / n\right)\right) s∗=round(log2(∥w^std∥1/n))
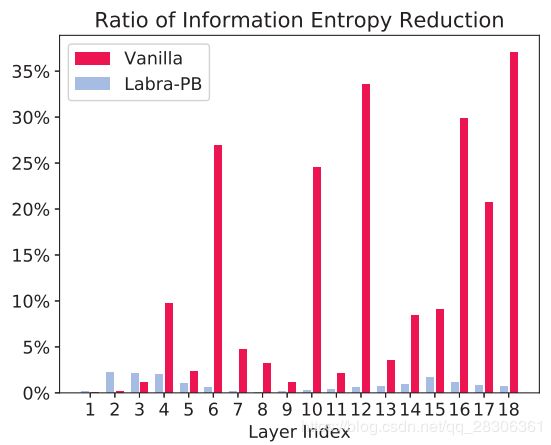
这个就是作者加上了“熵”之后得到的权重分布可以看到，加上了熵损失之后，二值化权重的熵是增加的，即表达能力是提升的。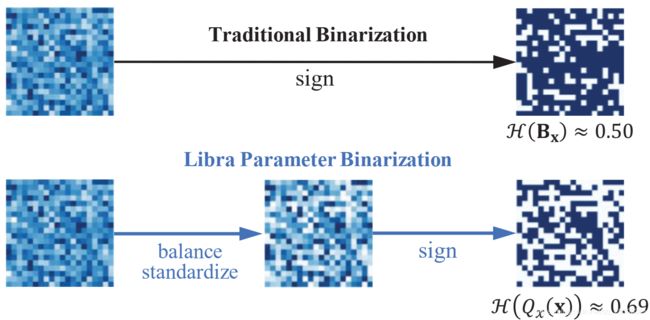
这个是作者使用ResNet-20在CIFAR上的结果，可以看到，加了Labra-PB之后，即使对于很深的层，熵的损失也比较小。
Error Decay Estimator in Backward Propagation
由于量化带来了数值不连续的问题，所求的梯度也是近似的，这样就带来了信息丢失的问题。一般而言，标准的梯度计算应该是： ∂ L ∂ w = ∂ L ∂ Q w ( w ^ s t d ) ∂ Q w ( w ^ s t d ) ∂ w ≈ ∂ L ∂ Q w ( w ^ s t d ) g ′ ( w ) \frac{\partial \mathcal{L}}{\partial \mathbf{w}}=\frac{\partial \mathcal{L}}{\partial Q_{w}\left(\hat{\mathbf{w}}_{\mathrm{std}}\right)} \frac{\partial Q_{w}\left(\hat{\mathbf{w}}_{\mathrm{std}}\right)}{\partial \mathbf{w}} \approx \frac{\partial \mathcal{L}}{\partial Q_{w}\left(\hat{\mathbf{w}}_{\mathrm{std}}\right)} g^{\prime}(\mathbf{w}) ∂w∂L=∂Qw(w^std)∂L∂w∂Qw(w^std)≈∂Qw(w^std)∂Lg′(w)其中 L ( w ) L(w) L(w)表示损失函数， g ( w ) g(w) g(w)表示 sign 函数的近似函数， g ′ ( w ) g^{\prime}(\mathbf{w}) g′(w)表示其导数。对于近似函数的选择，一般有两种： Identity : y = x o r Clip : y = Hardtanh ( x ) \textup{Identity}:y=x\, \, or \, \, \textup{Clip}:y=\textup{Hardtanh}(x) Identity:y=xorClip:y=Hardtanh(x)对于Identity函数，从它的图像可以看出，对于二值化以外的部分，它的梯度计算偏差太多。
对于Clip函数，它把clip范围外的数值的梯度都变成01了，更新不了，这个性质也不太好。
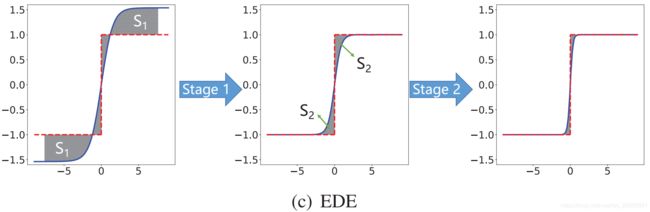
作者就将两者结合了一下，设计了Error Decay Estimator： g ( x ) = k tanh t x g(x)=k \tanh t x g(x)=ktanhtx其中， k k k和 t t t是随着训练时期变化的数值： t = T min 1 0 i N × log T max T min , k = max ( 1 t , 1 ) t=T_{\min } 10^{\frac{i}{N} \times \log \frac{T_{\max }}{T_{\min }}}, \quad k=\max \left(\frac{1}{t}, 1\right) t=Tmin10Ni×logTminTmax,k=max(t1,1)其中， T m i n = 1 0 − 1 T_{min}=10^{-1} Tmin=10−1， T m a x = 1 0 1 T_{max}=10^{1} Tmax=101。在训练的时候，EDE将训练分为两个阶段：
- Retain the updating ability of the backward propagation algorithm
将gradient estimation function的导数设置成一个接近1的数，然后将截断值从大变小，即逐步地从Identity function变成Clip function - Retain the accurate gradients for parameters around zero
将截断值保持为1，逐步将函数曲线变陡，让 Clip 函数逐渐接近 sign 函数。整个过程如下图所示。
整个算法的流程如下图所示：
Experiments
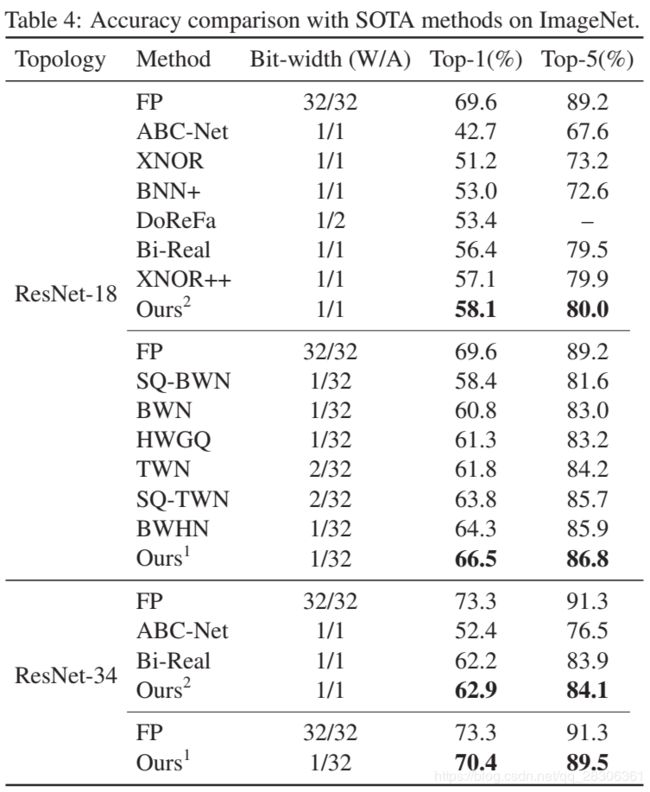
作者在测试的时候，没有量化第一层和最后一层，激活函数使用的是Hardtanh函数。在ImageNet上的部分结果如下所示。
Summary
感觉这个文章，综合了一些之前文章的优点，比如使用balanced weight，以及训练的时候，这种逐渐逼近的方法，之前也有类似的方案，对于损失函数中加入“熵”损失则是一项创新的亮点。