高效八叉树octree:基于hash函数的数据结构
1.基础知识
八叉树octree是一种递归、轴对齐且空间分隔的数据结构,常用于计算机几何来优化碰撞检测、最邻近搜索等,且常用于3D数据的表达。
一个八叉树结构,将有限的三维体数据等分为8个octants。octants也被称为nodes(节点,树结构概念中)或者cells(单元,空间概念中)。将空间分成等大小的立方体可以加速细分运算,且单元大小的存储也节省空间。
一个八叉树是通过递归的将空间细分成八个子单元,直到每个单元中剩余空间的大小在预定权值下,或者达到了最大树深度。每个单元都被单个轴对齐的平面细分的,类似于空间坐标系,其原点通常放在父节点的中心位置。(此处可思考不放在中心会怎么样)
因此,每个节点都可以有0或8个子节点。因此,相较于正常的网格结构,便于存储稀疏分布的结构。
2.octree的节点表达形式
传统基于指针的节点表达:
常用于octree需要频繁更新且内存消耗可以忍受的情况。通常,该节点结构体(104 byte)为:
// standard representation (104 byte)
struct OctreeNode
{
OctreeNode * Children[8];//8个子节点指针
OctreeNode * Parent; // optional 父节点指针
Object * Objects;//物体指针
Vector3 Center;//中心位置vector
Vector3 HalfSize;//octan大小vector
};位于中间位置的节点以上都有,但叶节点没有子节点。因此,还常常加一项bool Isleaf;
稍微节约一点的方式:不存储每个节点的指针,而是将8个子节点连续存储成一个块,只需要存储开头的指针就好了:
其结构体(49 byte):
// block representation (49 bytes)
struct OctreeNode
{
OctreeNode * Children;
OctreeNode * Parent; // optional
Object * FirstObj;
Vector3 Center;
Vector3 HalfSize;
bool IsLeaf;
};结合前两者:兄妹表达sibling-child
每个节点有两个指针,一个是NextSibling,指向父节点的下一个子节点的;一个是FirstChild,指向节点的第一个子节点。
// sibling-child representation (56 bytes)
struct OctreeNode
{
OctreeNode * NextSibling;
OctreeNode * FirstChild;
OctreeNode * Parent; // optional
Object * FirstObj;
Vector3 Center;
Vector3 HalfSize;
};简介高效的基于index索引的表达:
现在常用的高效的octree,其节点都用基于index索引的表达,引入哈希函数的,大大节省了内存和遍历消耗。
这种表达形式,不再存储其父节点、子节点的指针,而是在每个节点存储唯一的index索引,称为位置编码。
而且,所有八叉树节点都存在哈希映射中,允许根据位置编码直接访问任意节点。因为,应用哈希映射,非常容易的根据任意节点的父节点和子节点来推导计算出他的位置编码。为避免不需要的哈希映射寻找不存在的子节点,节点结构西可以通过bit-mask(比特掩码,即为每个位置设置0-1编码)来确定该子节点是否被分配了内存空间。其结构体(13 byte)为:
struct OctreeNode // 13 bytes
{
Object * Objects;
uint32_t LocCode; // or 64-bit, depends on max. required tree depth
uint8_t ChildExists; // optional
};位置编码:
每个octant都获得了一个0-7的数字(3-bit),依赖于节点相对于其父节点中心的相对位置关系。
可能的编码为:左下前000,右下前001,左下后010,右下后011,左上前100,右上前101,左上后110,右上后111,如下图:
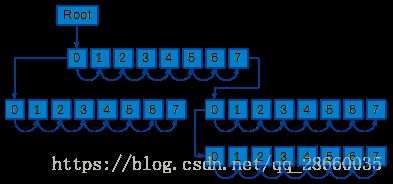
所以,任意树中子节点的位置编码都能,通过自上而下递归的计算并连接,所有节点的octant位置编码来表达其在octree中的位置。
为了根据位置编码来获得该节点所处树的深度,还需要设立一个标志位来表示位置编码的结束。因为,没有这种标志位,很难区分001和000001.通过使用1bit来mark序列的结束,1001可以轻松的区别于1000001,等于设立octree的根为1。1bit用于flag+每层3bit用于位置表示,所以32-bit的位置编码可以表示最大深度是10的octree。给定位置编码c,其处于树的level,深度值为![]()
size_t Octree::GetNodeTreeDepth(const OctreeNode *node)
{
assert(node->LocCode); // at least flag bit must be set
// for (uint32_t lc=node->LocCode, depth=0; lc!=1; lc>>=3, depth++);
// return depth;
#if defined(__GNUC__)
return (31-__builtin_clz(node->LocCode))/3;
#elif defined(_MSC_VER)
long msb;
_BitScanReverse(&msb, node->LocCode);
return msb/3;
#endif
}树遍历:
给定位置编码,沿octree向上或者向下移动,两步操作实现:1.获得下一个节点的位置编码;2.在哈希映射中寻找该节点。
为了能向上遍历octree。必须确定每个位置编码的父节点:只要去掉当前节点位置编码的最后3bit就行了:
class Octree
{
public:
OctreeNode * GetParentNode(OctreeNode *node)
{
const uint32_t locCodeParent = node->LocCode>>3;
return LookupNode(locCodeParent);
}
private:
OctreeNode * LookupNode(uint32_t locCode)
{
const auto iter = Nodes.find(locCode);
return (iter == Nodes.end() ? nullptr : &(*iter));
}
private:
std::unordered_map Nodes;
}; 为了能向下遍历octree。必须确定每个位置编码的子节点:只要在当前节点位置编码的最后3bit加上相应的子节点位置编码就行了:
void Octree::VisitAll(OctreeNode *node)
{
for (int i=0; i<8; i++)
{
if (node->ChildExists&(1<LocCode<<3)|i;
const auto *child = LookupNode(locCodeChild);
VisitAll(child);
}
}
} 完整的octree:
完整的八叉树,每个中间节点都有8个子节点,所有叶节点都有相同的树深度D,叶节点数 ,等于用 的分辨率细化了一个三维网格。所有节点数量为![]()
但我们一般用octree,都不是完整的,完整的就等效于一般网格了,没必要用了。一般都是使用其对稀疏数据表达的强大能力。