低通滤波器和高通滤波器的程序实现原理推导

傅立叶变换,拉普拉斯变换和Z变换

对于信号分析而言,傅立叶变换是必不可少的,我们都知道傅立叶变换是把系统从时域变换到频域进行分析,那么拉普拉斯变换和Z变换是干什么的?简单的来说,由于傅里叶变换的收敛有一个狄利克雷条件，要求信号绝对可积/绝对可和。对于那些不符合狄利克雷条件的信号该怎么办呢,我们将频域的概念扩展到复频域.首先要说明的是傅立叶变换大致有两种,连续时间的傅立叶变换(CTFT)和离散的傅立叶变换(DTFT).而对于CTFT而言,拉普拉斯变换就是将连续时间系统的傅立叶变换扩展了;而对于DTFT而言,Z变换就是将离散时间系统的傅立叶变换扩展了.知乎上有一个很好的对三种变换的解释:傅立叶变换、拉普拉斯变换、Z变换的联系

---

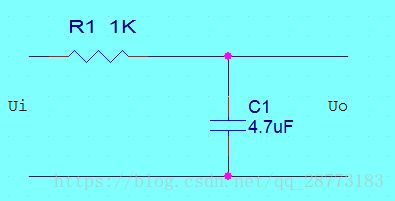
RC一阶低通滤波器的算法推导

一阶的RC电路如下:

这里直接给出其s域的传递函数:

VoutVin=1RCs+1,(s=jω) V o u t V i n = 1 R C s + 1 , ( s = j ω )

对其进行z变换(一阶后差分):
s=1−z−1T,T表示采样周期 s = 1 − z − 1 T , T 表 示 采 样 周 期
则传递函数变为:

Y(z)X(z)=TRC(1−Z−1)+T Y ( z ) X ( z ) = T R C ( 1 − Z − 1 ) + T

又因为 Y(z)=Y(n)z−n,且Y(n−1)Y(n)=z−1 Y ( z ) = Y ( n ) z − n , 且 Y ( n − 1 ) Y ( n ) = z − 1 , X(z)=X(n)z−n,且X(n−1)X(n)=z−1 X ( z ) = X ( n ) z − n , 且 X ( n − 1 ) X ( n ) = z − 1 ,代入到上式的传递函数得:

Y(n)=TT+RCX(n)+RCT+RCY(n−1) Y ( n ) = T T + R C X ( n ) + R C T + R C Y ( n − 1 )

其中:
X(n):本次采样值 X ( n ) : 本 次 采 样 值
Y(n−1):上次滤波值 Y ( n − 1 ) : 上 次 滤 波 值
令 a=TT+RC≈TRC=ωT=2πfT a = T T + R C ≈ T R C = ω T = 2 π f T
则滤波公式为:

Y(n)=a∗X(n)+(1−a)∗Y(n−1) Y ( n ) = a ∗ X ( n ) + ( 1 − a ) ∗ Y ( n − 1 )

这与px4代码的lib库中低通滤波是一样的:

float BlockLowPass::update(float input)
{
    if (!PX4_ISFINITE(getState())) {
        setState(input);
    }

    float b = 2 * float(M_PI) * getFCut() * getDt();
    float a = b / (1 + b);
    setState(a * input + (1 - a)*getState());//input:本次采样值 getState():上次滤波值
    return getState();
}

---

一阶RC高通滤波器

RC高通滤波器原理图如下,它和低通相反,电阻两端的电压作为输出,则其s域的传递函数为:

VoutVin=RCsRCs+1 V o u t V i n = R C s R C s + 1

z z 变换(一阶后向差分):

s=1−z−1T s = 1 − z − 1 T

得到 z z 域的传递函数为:

Y(z)X(z)=RC(1−z−1)RC(1−z−1)+T Y ( z ) X ( z ) = R C ( 1 − z − 1 ) R C ( 1 − z − 1 ) + T

同样的, Y(z)=Y(n)z−n,且Y(n−1)Y(n)=z−1 Y ( z ) = Y ( n ) z − n , 且 Y ( n − 1 ) Y ( n ) = z − 1 , X(z)=X(n)z−n,且X(n−1)X(n)=z−1 X ( z ) = X ( n ) z − n , 且 X ( n − 1 ) X ( n ) = z − 1 ,则有:

Y(n)=RCRC+T(X(n)−X(n−1)+Y(n−1)) Y ( n ) = R C R C + T ( X ( n ) − X ( n − 1 ) + Y ( n − 1 ) )

其中:
X(n):本次采样值 X ( n ) : 本 次 采 样 值
X(n−1):上次采样值 X ( n − 1 ) : 上 次 采 样 值
Y(n−1):上次滤波值 Y ( n − 1 ) : 上 次 滤 波 值
我们令令 b=TT+RC≈TRC=ωT=2πfT b = T T + R C ≈ T R C = ω T = 2 π f T , a=11+b a = 1 1 + b
则高通滤波的算法公式为:

Y(n)=b∗(X(n)−X(n−1)+Y(n−1)) Y ( n ) = b ∗ ( X ( n ) − X ( n − 1 ) + Y ( n − 1 ) )

这与px4中的高通滤波是一样的:

float BlockHighPass::update(float input)
{
    float b = 2 * float(M_PI) * getFCut() * getDt();
    float a = 1 / (1 + b);
    setY(a * (getY() + input - getU()));//getY():上次滤波器输出值;getU():上次滤波器输入值
    setU(input);
    return getY();
}

---

总结

关于低通滤波和高通滤波,最关键的是学到了三类变换的关系以及离散化的方法,留下各位大佬的博客链接在此:
【滤波器学习笔记】一阶RC低通滤波
傅立叶变换、拉普拉斯变换、Z变换的联系
基础电路—RC组成的低通、高通滤波器
双线性变换
z变换