数据结构与算法 -- 再论递归
之前在总结函数的时候,有介绍过递归。参看:C语言再学习 -- 函数 正在看数据结构与算法分析,开篇就讲到递归,那现在就详细讲解下它吧。
参看:递归函数理解
一、什么是递归函数
(1)递归函数即自调用函数,在函数内部直接或间接地自己调用自己,即函数的嵌套调用是函数本身。
从字面上来看递归,递即递推,采用循环的思路来描述复杂问题的方法。在递推阶段每一个递归调用通过进一步调用自己来记住这次递归过程,当其中调用满足终止条件时,递推结束。归即回归,函数调用已逆序的方式回归,知道最初调用的函数返回为止,此时递归过程结束。举个例子:
//示例一
#include
void show (int);
int main (void)
{
show (1);
return 0;
}
void show (int n)
{
printf ("Level %d: n location %p\n", n, &n);
if (n < 4)
show (n + 1);
printf ("Level %d: n location %p\n", n, &n);
}
执行结果如下:
Level 1: n location 0xbf8bf680
Level 2: n location 0xbf8bf660
Level 3: n location 0xbf8bf640
Level 4: n location 0xbf8bf620
Level 4: n location 0xbf8bf620
Level 3: n location 0xbf8bf640
Level 2: n location 0xbf8bf660
Level 1: n location 0xbf8bf680
//示例二
/*
6*5*4*3*2*1=?的阶乘
*/
#include
int func(int num) //整数类型
{
if(num==1)
{
return 1;
}
return num*func(num-1);
}
int main()
{
int num=func(6);
printf("6的阶乘为%d\n",num);
return 0;
}
输出结果:
6的阶乘为720
(2)递归的基本原理
第一:每一级的函数调用都有自己的变量。
第二:每一次函数调用都会有一次返回。
第三:递归函数中,位于递归调用前的语句和各级被调用函数具有相同的执行顺序。
第四:递归函数中,位于递归调用后的语句的执行顺序和各个被调用函数的顺序相反。
第五:虽然每一级递归都有自己的变量,但是函数代码并不会得到复制。
最后:递归函数中必须包含可以终止递归调用的语句。
(3)递归的优缺点
其优点在于为某些变成问题提供了最简单的解决方法,简化了程序设计。而缺点是一些递归算法会很快耗尽计算机的内存资源。同时,使用递归的程序难于阅读和维护。
二、函数调用机制的说明
任何函数之间不能嵌套定义,调用函数与被调用函数之间相互独立递归函数的概念用法与实例(彼此可以调用)。发生函数调用时,被调用函数中保护了调用函数的运行环境和返回地址,使得调用函数的状态可以被调用函数运行返回完全恢复,而且该状态与被调用函数无关。
被调用函数运行的代码虽然是同一个函数的代码体,但由于调用点,调用时状态,返回点的不同,可以看作是函数的一个副本,与调用函数的代码无关,所以函数的代码是独立的。被调用函数运行的栈空间独立于调用函数的栈空间,所以与调用函数之间的数据也是无关的。函数之间考参数传递和返回值来联系,函数看作为黑盒。
这种机制决定了 C/C++ 允许函数递归调用。
上面这段话的意思可以理解为,递归函数调用自身函数的时候,可以看作调用的是调用别的函数。
再有,被调用函数运行的栈空间独立于调用函数的栈空间 这句话如何理解?
首先,我们先说一下栈的概念:
参看:递归函数的概念用法与实例
参看:C语言再学习 -- 内存管理
栈是一个后进先出(LIFO)的压入(push)和弹出(pop)式的数据结构。在程序运行时,系统每次向栈中压入一个对象,然后栈指针向下移动一个位置。当系统从栈中弹出一个对象时,最近进栈的对象将被弹出。然后栈指针向上移动一个位置。程序员经常利用栈这种数据结构来处理那些最适合用后进先出逻辑来描述的编程问题。这里讨论的程序中的栈每个程序中都是存在的,它不需要程序员编写代码去维护,而是由运行时系统自动处理。所谓系统自动维护,实际上就是编译器所产生的程序代码。尽管在程序中看不到他们,但是程序员应该对此有所了解。
再看看程序中的栈是如何工作的。当一个函数(调用者)调用另一个函数(被调用者)时,运行系统将把调用者的所有实参和返回地址压入栈中,栈指针将移到合适的位置来容纳这些数据。最后进栈的是调用者的返回地址。当被调用这开始执行时,系统把被调用者的自变量压入栈中,并把栈指针再向下移,以保证有足够的空间存储被调用这声明的所有自变量。当调用这把实参压入栈后,被调用者就在栈中以自变量的形式建立形参。被调用这内部的其他自变量也是存放在栈中的。由于这些进栈操作,栈指针已经移动所有这些局部变量之下。但是被调用者记录了它刚开始执行时的初始栈指针,以它为参考,用正或负的偏移量来访问栈中的变量。当被调用者准备返回时,系统弹出栈中所有的自变量,这是栈指针移动了被调用者刚开始执行时的位置。接着被调用者返回,系统从栈中弹出返回地址,调用者就可以继续执行了。当调用者继续执行时,系统还将从栈中弹出调用者的实参,于是栈指针回到了调用发生前的位置。
想深入了解栈和递归的关系,参看:C语言数据结构----栈与递归
现在接着说递归:
上面有提到了函数调用机制。递归之所以能实现,是因为函数的每个执行过程都在栈中有自己的形参和局部变量的拷贝,这些拷贝和函数的其他执行过程毫不相干。这种机制是当代大多数程序设计语言实现子程序结构的基础,是使得递归成为可能。假定某个调用函数调用了一个被调用函数,再假定被调用函数又反过来调用了调用函数。这第二个调用就被称为调用函数的递归,因为它发生在调用函数的当前执行过程运行完毕之前。而且,因为这个原先的调用函数、现在的被调用函数在栈中较低的位置有它独立的一组参数和自变量,原先的参数和变量将不受影响,所以递归能正常工作。程序遍历执行这些函数的过程就被称为递归下降。
程序员需保证递归函数不会随意改变静态变量和全局变量的值,以避免在递归下降过程中的上层函数出错。程序员还必须确保有一个终止条件来结束递归下降过程,并且返回到顶层。看下面的例子:
/*实现 1+2+3+4+5 = ?*/
//使用 static int num = 0;
#include
int add (int);
int main (void)
{
add (1);
}
int add (int num)
{
static int sum = 0;
sum += num;
printf ("sum = %d, num = %d\n", sum, num);
if (num == 5)
return ;
add (++num);
}
输出结果:
sum = 1, num = 1
sum = 3, num = 2
sum = 6, num = 3
sum = 10, num = 4
sum = 15, num = 5 这里有一个问题一定要注意,就是static int sum = 0;
有些人就不明白,为什么要使用 static 类型修饰符,为什么不使用 int sum=0;?如果使用 int sum=0; 这样的语句,在每次调用函数add()的时候,sum的值都是赋值为0,也就是第一步虽然加了1上来,可是第二次调用的时候,sum又回到了0。我们前面说了,static能保证本次初始化的值是上次执行后的值,这样也就保证了前面想加的结果不会丢失。如果你修改为int sum=0,最后结果一定是最后结果是5而不是15。
/*实现 1+2+3+4+5 = ?*/
//使用 int sum = 0;
#include
int add (int);
int main (void)
{
add (1);
}
int add (int num)
{
int sum = 0;
sum += num;
printf ("sum = %d, num = %d\n", sum, num);
if (num == 5)
return ;
add (++num);
}
输出结果:
sum = 1, num = 1
sum = 2, num = 2
sum = 3, num = 3
sum = 4, num = 4
sum = 5, num = 5 上面的例子就很好的解释了,被调用函数运行的栈空间独立于调用函数的栈空间 这句话。
三、递归调用的形式
/*
6*5*4*3*2*1=?的阶乘
*/
#include
int func(int num) //整数类型
{
if(num==1)
{
return 1;
}
return num*func(num-1);//直接递归
}
int main()
{
int num=func(6);
printf("6的阶乘为%d\n",num);
return 0;
}
输出结果:
6的阶乘为720 #include
int foo (int x)
{
printf ("x = %d\n", x);
if (x <= 0)
return x;
return bar (x); //间接递归
}
int bar (int y)
{
return foo (y - 1);
}
int main (void)
{
foo (5);
return 0;
}
输出结果:
x = 5
x = 4
x = 3
x = 2
x = 1
x = 0 #include
int func(int num, int n)
{
if(num == 1)
{
return n;
}
return func(num-1, num*n);//尾递归
}
int main()
{
int num=func(6, 1);
printf("6的阶乘为%d\n",num);
return 0;
}
输出结果:
6的阶乘为720
#include
void recurse(int count)
{
printf("%d \n",count);
return recurse(count + 1); //递归
}
int main()
{
recurse(1);
}
输出结果:
...
261929
261930
261931
261932
261933
261934
261935
段错误 (核心已转储) #include
int func(int num)
{
int n = 1, m = 1;
for (n = 1; n <= num; n++)
{
m = m*n;
}
return m;
}
int main()
{
int num=func(6);
printf("6的阶乘为%d\n",num);
return 0;
}
输出结果:
6的阶乘为720 递归中一定有迭代,但是迭代中不一定有递归,大部分可以相互转换。能用迭代的不用递归,递归调用函数,浪费空间,并且递归太深容易造成堆栈的溢出。
循环:不变的重复。
个人认为迭代是循环的一种,循环体代码分为固定循环体,和变化的循环体。
#include
int main()
{
int i = 0;
for (i = 0; i <= 5; i++)
{
printf ("hello world!\n");
}
return 0;
}
输出结果:
hello world!
hello world!
hello world!
hello world!
hello world!
hello world! #include
int main()
{
int i = 0;
int sum = 0;
for (i = 0; i <= 5; i++)
{
sum += i;
}
printf ("sum = %d\n", sum);
return 0;
}
输出结果:
sum = 15
迭代的好处:迭代减少了冗余代码,提高了代码的利用率和动态性。
//递归
#include
#include
long long getSystemTime() {
struct timeb t;
ftime(&t);
return (1000 * t.time + t.millitm);
}
int fibonacci(int n)
{
if( n > 1 )
{
return fibonacci(n-1) + fibonacci(n-2);
}
else if( n == 1 )
{
return 1;
}
else if( n == 0 )
{
return 0;
}
}
int main()
{
int i = 0;
long long start = getSystemTime();
for(i=1; i<=40; i++)
{
printf("fibonacci(%d) = %d\n", i, fibonacci(i));
}
long long end = getSystemTime();
printf("time: %lld ms\n", end-start);
return 0;
}
输出结果:
time: 4836 ms
//迭代
#include
#include
#include
long long getSystemTime() {
struct timeb t;
ftime(&t);
return (1000 * t.time + t.millitm);
}
int fibonacci(int n)
{
if (n == 1 || n == 0)
return n;
int *arr = (int*)malloc(sizeof (int)*n + 1);
arr[1] = 1;
arr[2] = 1;
int i = 0;
for (i = 3;i <=n; i++)
{
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n];
}
int main()
{
int i = 0;
long long start = getSystemTime();
for(i=1; i<=10; i++)
{
printf("fibonacci(%d) = %d\n", i, fibonacci(i));
}
long long end = getSystemTime();
printf("time: %lld ms\n", end-start);
return 0;
}
输出结果:
time: 1 ms 四、递归四条基本法则
#include
void show (int);
int main (void)
{
show (1);
return 0;
}
void show (int n)
{
printf ("Level %d: n location %p\n", n, &n);
if (n < 4)
show (n + 1);
printf ("Level %d: n location %p\n", n, &n);
}
执行结果如下:
Level 1: n location 0xbf8bf680
Level 2: n location 0xbf8bf660
Level 3: n location 0xbf8bf640
Level 4: n location 0xbf8bf620
Level 4: n location 0xbf8bf620
Level 3: n location 0xbf8bf640
Level 2: n location 0xbf8bf660
Level 1: n location 0xbf8bf680 例如,下面的代码无条件调用函数自己,造成无限制递归,终将使栈空间溢出:
#include
void count(int val)
{
count(val-1); //无限制递归
if(val>1) //该语句无法到达
printf ("ok\n");
}
int main (void)
{
count (10);
return 0;
}
输出结果:
段错误 (核心已转储) 五、递归进阶篇
关于递归理论知识上面总结的已经很全面了。下面讲一些利用递归解决问题的例程。
1、斐波那切数列
虽然之前说过,使用递归解决斐波那切数列,只能说脑子被驴踢了。但是它毕竟提供了一种解题思想。
首先了解下斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55,...
在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
所以也就有了下面的递归写法:
//递归
#include
int fibonacci (int n)
{
if (n == 0)
return 1;
else if (n == 1)
return 1;
else if (n >= 2)
return fibonacci (n - 1) + fibonacci (n - 2);
}
int main (void)
{
int i = 0;
for(i = 0; i < 10; i++)
printf ("fibonacci (%d) = %d\n", i, fibonacci (i));
return 0;
}
输出结果:
fibonacci (0) = 1
fibonacci (1) = 1
fibonacci (2) = 2
fibonacci (3) = 3
fibonacci (4) = 5
fibonacci (5) = 8
fibonacci (6) = 13
fibonacci (7) = 21
fibonacci (8) = 34
fibonacci (9) = 55
当然,如果 n 比较大的情况下还是推荐使用迭代。
2、国王被“数字”欺骗的故事
传说,舍罕王要重赏国际象棋的发明人——宰相达依尔.达依尔指着国际象棋的棋盘说:“陛下,请您在这张棋盘的第一
小格内,赏给我一粒麦子,第二小格内给二粒麦子,第三小格内给四粒麦子,照这样下去,每一小格内的麦粒都比前一小格增
加一倍.然后把这棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王命令仆人把一袋麦子拿高棋盘前,但是,还没有放
到第20格,袋子已经 空了.于是,麦子一袋一袋地扛进来,结果仓库也空了,棋盘上的格子还没有全部放上麦粒呢!舍罕王这
才想到受骗了.算一算,麦粒放到第()格,这一格的麦粒已经超过一亿粒;第64格大约要放()亿粒.
这个故事从小就听过了,结果是:1, 2, 4, 8, 16, 32, ....
如果以递归的方式定义:F(0)=1,F(1)=2, F(n)=F(n-1)*2 (n > 1)
所以也就有了下面的递归写法:
//递归
#include
int foo (int n)
{
if (n == 0)
return 1;
else if (n == 1)
return 2;
else if (n > 1)
return foo (n - 1) * 2;
}
int main (void)
{
int i = 0, sum = 0;
for(i = 0; i < 10; i++)
{
printf ("foo (%d) = %d\n", i, foo (i));
sum += foo (i);
}
printf ("总和为:%d\n", sum);
return 0;
}
输出结果:
foo (0) = 1
foo (1) = 2
foo (2) = 4
foo (3) = 8
foo (4) = 16
foo (5) = 32
foo (6) = 64
foo (7) = 128
foo (8) = 256
foo (9) = 512
总和为:1023
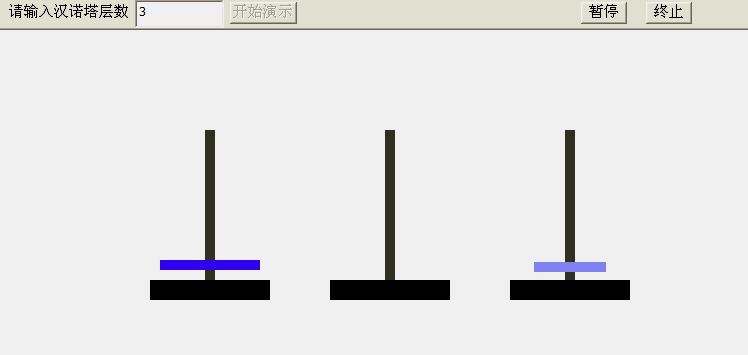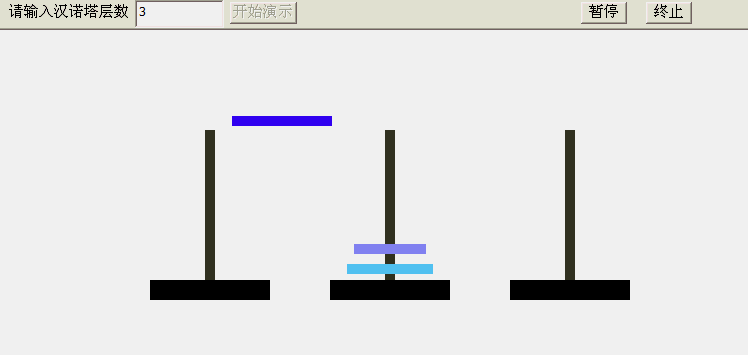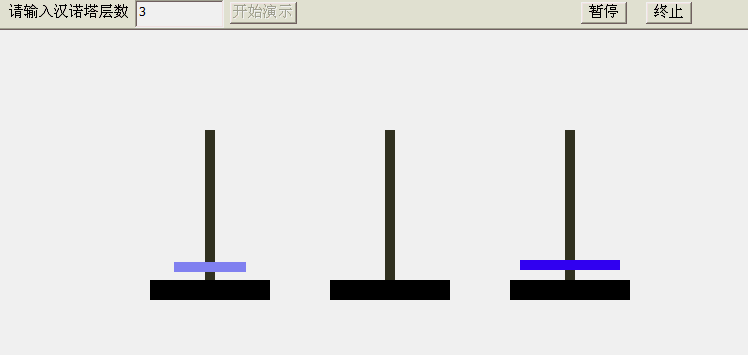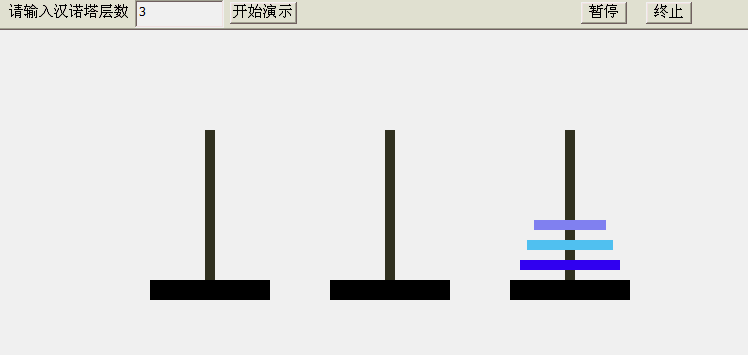
3、汉诺塔的故事
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。大梵天命令婆罗
门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一
次只能移动一个圆盘。
具体游戏怎么玩我就不说了,感兴趣的可以玩两把:新汉诺塔
所以也就有了下面的递归写法:
参看:经典递归解决汉诺塔!
#include
//第一个塔为初始塔,中间的塔为借用塔,最后一个塔为目标塔
int i = 1; //记录步数
void move (int n, char from, char to) //将编号为n的盘子由from移动到to
{
printf ("第%d步:将%d号盘子%c---->%c\n", i++, n, from, to);
}
void hanoi (int n, char from, char denpend_on, char to) //将n个盘子由初始塔移动到目标塔(利用借用塔)
{
if (n == 1)
move (1, from, to); //只有一个盘子是直接将初塔上的盘子移动到目的地
else
{
hanoi (n - 1, from, to, denpend_on); //先将初始塔的前n-1个盘子借助目的塔移动到借用塔上
move (n, from, to); //将剩下的一个盘子移动到目的塔上
hanoi (n - 1, denpend_on, from, to); //最后将借用塔上的n-1个盘子移动到目的塔上
}
}
int main (void)
{
printf ("请输入盘子的个数:\n");
int n;
scanf ("%d", &n);
char x = 'A', y = 'B', z = 'C';
printf ("盘子移动情况如下:\n");
hanoi (n, x, y, z);
}
输出结果:
请输入盘子的个数:
3
盘子移动情况如下:
第1步:将1号盘子A---->C
第2步:将2号盘子A---->B
第3步:将1号盘子C---->B
第4步:将3号盘子A---->C
第5步:将1号盘子B---->A
第6步:将2号盘子B---->C
第7步:将1号盘子A---->C 4、全排列
#include
int main (void)
{
int temp = 0;
int a = 10, b = 5;
printf ("a = %d, &a = %p\n", a, &a);
printf ("b = %d, &b = %p\n", b, &b);
printf ("temp = %d, &temp = %p\n", temp, &temp);
printf ("\n------------------------\n");
temp = a;
a = b;
b = temp;
printf ("a = %d, &a = %p\n", a, &a);
printf ("b = %d, &b = %p\n", b, &b);
printf ("temp = %d, &temp = %p\n", temp, &temp);
return 0;
}
输出结果:
a = 10, &a = 0xbffd3b98
b = 5, &b = 0xbffd3b9c
temp = 0, &temp = 0xbffd3b94
------------------------
a = 5, &a = 0xbffd3b98
b = 10, &b = 0xbffd3b9c
temp = 10, &temp = 0xbffd3b94 #include
//此处为引用,交换函数.函数调用多,故定义为内联函数.
void swap (char *a , char *b)
{
char temp ;
temp = *a;
*a = *b;
*b = temp;
}
void perm (char list[], int k, int m) //k表示前缀的位置,m是要排列的数目.
{
int i;
if(k == m -1) //前缀是最后一个位置,此时打印排列数.
{
for(i = 0; i < m ;i++)
printf ("%c", list[i]);
printf ("\n");
}
else
{
for(i = k ;i < m; i++)
{
//交换前缀,使之产生下一个前缀.
swap (&list[k], &list[i]);
perm (list, k + 1, m);
//将前缀换回来,继续做上一个的前缀排列.
swap (&list[k], &list[i]);
}
}
}
int main (void)
{
char list[] ="123";
perm (list, 0, 3);
return 0;
}
输出结果:
123
132
213
231
321
312 0
1
123
2
132
1
1
213
2
231
2
1
321
2
312#include
void Permutation(char* pStr, char* pBegin);
void permutation(char* pStr)
{
Permutation(pStr, pStr);
}
void swap (char *a, char *b)
{
char temp;
temp = *a;
*a = *b;
*b = temp;
}
void Permutation(char* pStr, char* pBegin)
{
char *pCh;
if(!pStr || !pBegin)
return;
if(*pBegin == '\0')
{
printf("%s\n", pStr);
}
else
{
for(pCh = pBegin; *pCh != '\0'; pCh++)
{
// swap pCh and pBegin
swap (pCh, pBegin);
Permutation(pStr, pBegin + 1);
// restore pCh and pBegin
swap (pCh, pBegin);
}
}
}
int main()
{
char str[] ="123";
permutation(str);
return 0;
}
输出结果:
123
132
213
231
321
312 5、strlen函数实现
#include
int strlen (const char *s)
{
const char *sc = s;
int cnt = 0;
while (*sc != '\0')
{
sc++;
cnt++;
}
return cnt;
}
int main (void)
{
printf ("%d\n", strlen ("12345"));
return 0;
}
输出结果:
5 #include
int strlen (const char *s)
{
if (NULL == s)
return -1;
else if (*s == '\0')
return 0;
else
return strlen (s + 1) + 1;
}
int main (void)
{
printf("strlen(\"12345\") = %d\n", strlen("12345"));
printf("strlen(NULL) = %d\n", strlen(NULL));
printf("strlen(\"\") = %d\n", strlen(""));
return 0;
}
输出结果:
strlen("12345") = 5
strlen(NULL) = -1
strlen("") = 0