【算法】震惊!!!史上最详细的卡特兰数浅谈!!!
我是标题党
卡特兰数简介
卡特兰数是组合数学中的一种著名数列,通常用如下通项式表示(为了不与组合数 C C C冲突,本文用 f f f表示卡特兰数):
f ( n ) = C 2 n n n + 1 f(n)=\frac{C_{2n}^{n}}{n+1} f(n)=n+1C2nn
当然,卡特兰数也是有递推式的:
f ( n ) = ∑ i = 0 n − 1 f ( i ) × f ( n − i − 1 ) f(n)=\sum_{i=0}^{n-1}f(i)\times f(n-i-1) f(n)=i=0∑n−1f(i)×f(n−i−1)
但在实际应用中,最常用的却是第一个通项式的变形:
f ( n ) = C 2 n n − C 2 n n − 1 f(n)=C_{2n}^{n}-C_{2n}^{n-1} f(n)=C2nn−C2nn−1
卡特兰数的应用
基本模型
有一个长度为 2 n 2n 2n的01序列,其中1,0各 n n n个,要求对于任意的整数 k ∈ [ 1 , n ] k \in [1,n] k∈[1,n],数列的前 k k k个数中,1的个数不少于0。
解决方法
当然你可以选择用DP秒切。
不知当初哪位神仙想出了这种神奇的构造方法。
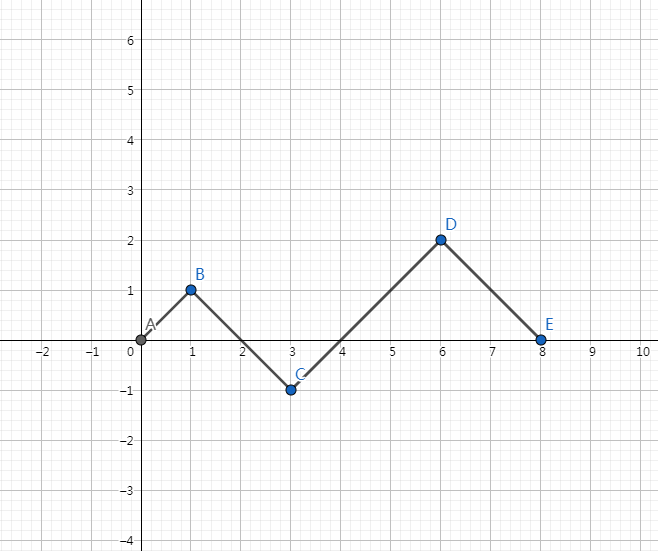
我们把0,1操作扔到一个坐标系中。1看成向右上方走一步,0看成向右下角走一步,那么最后构造完后一定走到了 ( 2 n , 0 ) (2n,0) (2n,0)
如下图:
那么总的路径数量就是在 2 n 2n 2n步中选择 n n n步为1,方案数为 C 2 n n C_{2n}^{n} C2nn。
接着来考虑题目中的限制条件:对于任意前缀,1的个数不少于0。
那么转化到坐标系中,也就是说走的路径不应该穿过 x x x轴,即直线 y = 0 y=0 y=0,也就是不接触 y = − 1 y=-1 y=−1。
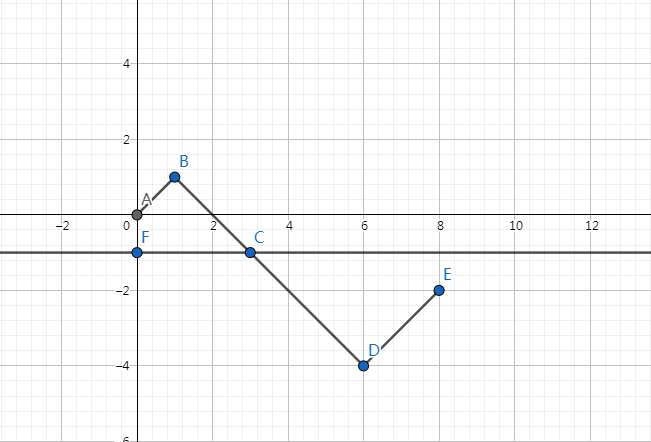
于是我们把与 y = − 1 y=-1 y=−1的接触点的右边整条路径以 y = − 1 y=-1 y=−1为对称轴翻折,于是终点变为了 ( 2 n , − 2 ) (2n,-2) (2n,−2)。如下图:
那么此时,从 ( 0 , 0 ) (0,0) (0,0)到 ( 2 n , − 2 ) (2n,-2) (2n,−2)的路径必定至少穿过一次 y = − 1 y=-1 y=−1,不满足条件,那么此时的路径数量即为总路径数中不符合题意的路径数,那么我们用总路径数减去不符合的路径数,就是最终的答案。
而此时的路径数量也很简单,由于反转后终点向下移了两位,也就意味着 n − 1 n-1 n−1步是1, n + 1 n+1 n+1步是0,总方案为 C 2 n n − 1 C_{2n}^{n-1} C2nn−1,那么最终的答案就是 C 2 n n − C 2 n n − 1 C_{2n}^{n}-C_{2n}^{n-1} C2nn−C2nn−1。
诶,这不就是卡特兰数吗。
例题
- 洛谷1641 生成字符串
- Loj10238网格
这两道题需要在深刻理解了上述卡特兰数的推导后进行一些变形得出最终的答案。
具体的变动在于,转换成基本模型后,1和0的个数不一样,分别为 n n n和 m m m,最后可以得出答案为 C n + m n − C n + m m − 1 C_{n+m}^{n}-C_{n+m}^{m-1} Cn+mn−Cn+mm−1。白水一道紫题。
- 洛谷P2532 树屋阶梯
这道题我一看两军阵前……,跟卡特兰数好像没有直接关系,但是手画几个样例后,发现答案都是卡特兰数,那么基本上就可以大胆猜想了。
但实际上,我们可以从 d p dp dp的角度考虑这道题。对于任意大小为 n n n的阶梯,我们都可以现在左下角放一个大块,然后在上方构造一个大小为 i i i的阶梯,右下方构造大小为 n − i − 1 n-i-1 n−i−1的阶梯,那么转移方程就十分显然:
f ( n ) = ∑ i = 0 n − 1 f ( i ) ∗ f ( n − i − 1 ) f(n)=\sum_{i=0}^{n-1}f(i)*f(n-i-1) f(n)=i=0∑n−1f(i)∗f(n−i−1)
显然就是卡特兰数,直接一波通项式+高精度搞定。
- 洛谷P3200 有趣的数列
首先有一个结论,对于每个偶数位,上面放的数必须不小于当前位的下标。(意会一下)
转化一下题意:把1~2n这些数依次放入序列,每次可以选择最后的奇数位或偶数位。
然后再观察后发现一个显然的性质:对于任意时刻,数列中的奇数位数量不能少于偶数位数量。否则偶数位上放的数不可能大于等于下标。
于是,这就是一个卡特兰数模板,通项式秒切。具体对于组合数的处理,可以参看各种题解。