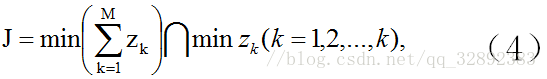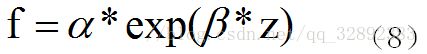基于改进遗传算法的双重路径约束下多AGV的路径规划
作者:Zengliang Han, Dongqing Wang ,Feng Liu,Zhiyong Zhao,翻译:Wu Xian
关键词:遗传算法,AGV,路径规划
原文网址:http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0181747
Multi-AGV path planning with double-pathconstraints by using an improved genetic algorithm
Abstract: Thispaper investigates an improved genetic algorithm on multiple automated guidedvehicle (multi-AGV) path planning. The innovations embody in two aspects. First,three-exchange crossover heuristic operators are used to produce more optimaloffsprings for getting more information than with the traditional two-exchangecrossover heuristic operators in the improved genetic algorithm. Second,double-path constraints of both minimizing the total path distance of all AGVsand minimizing single path distances of each AGV are exerted,gaining theoptimal shortest total path distance. The simulation results show that thetotal path distance of all AGVs and the longest single AGV path distance areshortened by using the improved genetic algorithm.
Key words: geneticalgorithm;AGV; path planning
1 多AGV路径规划问题
1.1 AGV系统相关问题
多目标的优化已经应用于包括工程、运输、物流等许多领域,所谓多目标问题就是寻找一个满足所有目标函数的解决方案。多目标优化方法包括经典优化算法(如加权和法,ε约束法,迭代法)和智能优化方法(如基于遗传进化的方法、基于种群的方法)。具有多目标性的多无人车系统,由于他们在工作站间的材料运输上的高效率,在物流配送领域正发挥着越来越重要的作用。
AGV系统的应用面临的几个重要问题:AGV的数量确定,路径规划和约束施加等等。确定车辆最优数量是AGV系统管理中的基本问题。为了解决这一问题,有几种方法被提出,它们的主要目标是利用足够数量的AGV及时执行所有任务。例如,Vivaldini等人提出了一种新的模型,通过整合任务分配和路由,来为一组任务的执行估计无人车的最优数量。冀和夏等人为AGV系统建立了一个新的模型,采用基于二分查找的近似解析法研究车辆最小数量。Koo等人研究了AGV车队尺寸模型,用等待时间来衡量各种车辆调度以确定合适的车队大小。
多AGV路径规划是保证物料在生产过程中高效流动的关键。路径规划涉及调度,行程安排,任务路线等三个问题。和旅行商问题类似,多AGV路径规划问题会在寻找最短路程(时间)方面,由于搜索空间太大而难以求解。Smolic-Rocak等人用向量形式的时间窗求解多AGV系统的最短路径问题。Draganjac等人提出了一种多AGV系统考虑非完全车辆约束的最短可行路径规划算法。王等人提出了一种基于生成优良个体的TSP多后代遗传算法。江和严为TSP开发了一种离散果蝇优化算法。
在多AGV路径规划中存在各种约束,例如无碰撞约束,时间窗约束,以及距离/时间约束。
1.2 算法简介
传统的遗传算法采用两个交换交叉算子进行交叉操作,即利用两个亲本个体来产生子代染色体。显然,传统的只有两个亲代个体而非多亲代个体的遗传算法,将获得较少的父信息,并且降低了子代性能的多样性。为了提高后代的多样性,我们提出了三交换交叉算子进行交叉操作,即采用三个父代个体产生的后代染色体。
区别于传统路径约束即只对全路径的总距离进行约束,新的算法对全AGV路径及每个AGV单路径进行双路径限制。该策略成倍缩短了总/单路径长度,并得到了最优结果。利用三个父代个体比其他传统的方法只有两个父代个体来产生的后代染色体,这种方法提高了生产后代的染色体信息,增加了获得继承父代优良特性的可能性并且加速了改进算法的搜索速度。对算法的仿真结果显示,相比传统遗传算法,改进后的算法能获得较短的全AGV路径总距离。
2 AGV工作空间建模
一个多AGV的车间制造系统担任物料输送的工作,有M个AGV工作于N个工作站之间。对于工作站的分配考虑以下方面:
• M个AGV往返于N个工作站之间(N>M);
• 只有一个AGV需要通过每个工作站(除了起点);
• 每个AGV从相同的起点(工作站)出发并回到起点;
• 每个AGV分别以预定的路径和固定的速度单独行进一条路线;
• 施加双重约束:所有AGV路径总距离应最小化同时每个AGV单路径距离应尽量小。
如图1所示
图1无人车系统工作路线图
Fig.1 Thework diagram of the AGV system
用符号表示
目标函数:
条件:式(5)指定每个AGV从启动站0开始,所有工作站只能通过AGV访问一次;式(6)表示任何路径都是从启动工作站开始,式(7)说明同样以起点为结束。
3 算法设计
采用遗传算法进行多AGV路径规划的关键问题是采用有效的编码和解码方法。遗传算法反复地选择、交叉和变异人口,以产生新一代的人口,比父母更适应环境,直到满足所需的要求。遗传算法的步骤包括:遗传编码、种群选择、适应度函数、选择操作、交叉操作和矩阵译码。
3.1 遗传编码
对N个运输工作站分别记为1,2,…,N,并增加M-1个虚拟标记,代表M-1个虚拟位置,分别标记为N+1,...,N+M-1。这些虚拟标记与起始点一致,代表每当出现一个虚拟符号时,相应的AGV返回到起始点。假设一个基因代表一个单AGV运行路径,一条染色体中包含的所有基因,即所有AGV的运动路径。为了避免子路径的频繁出现,设起始点0到起点0的路径距离是无限的。
例如,有10个工作站,其代码是0-9,由5台AGV完成任务,一个随机的染色体编码如图2所示
图2一条随机染色体
Fig. 2 A random chromosome
5辆AGV的路径如下:
0—6—2—0
0—7—0
0—1—8—0
0—3—4—0
0—5—9—0
在迭代过程中,可能会有两种不可行的方案,如图3、4所示。
图3 不可行情况1
Fig. 3 Situation 1 of dead solutions
图4 不可行情况2
Fig .4 Situation 2 of dead solutions
1. 虚拟符号出现在染色体的一端
情况1下,5辆AGV的路径如下:
0—0—0
0—2—6—7—0
0—1—8—0
0—3—4—0
0—5—9—0
0—0—0路径的距离是无限的,并不能满足距离最小化约束,所以这个染色体将会被淘汰。
2. 虚拟符号不断出现在一条染色体上
情况2下,5辆AGV的路径如下:
0—6—2—0
0—7—8—1—0
0—0—0
0—3—4—0
0—5—9—0
显然,0—0—0路径的染色体并不能满足最小化距离约束,所以这个染色体也会被淘汰。
3.2 群体选择
适当的种群规模对遗传算法收敛性是很重要的。如果种群规模太小,遗传算法很容易得到局部最优解,反之,如果种群规模过大,则遗传算法的计算速度会降低。种群规模与N有关,适当的种群规模应控制在4N和6N之间。
3.3 适应度函数
这里采用指数适应度函数,该方法思想来自SA(模拟退火)过程。由于以指数规模变换的优势,这里选择一种指数变换的适应函数。
其中z(=z1+z2+zk)是其中的一个父代个体;α和β是运算常量,α决定强制复制程度,值越小,则以最大适应值的个体的复制强度越大。
3.4 选择操作
选择操作决定再结合或交叉父代个体和预定种群产生的后代个体数量。选择操作会直接影响遗传算法的结果。不合适的选择操作将造成进化终止或使算法丧失多样性,造成早熟问题。这里采用轮盘赌轮选择父代个体,个体i的概率等于其适应值与群体适应值和的比值,如下式所示。

3.5 交叉操作
传统上,交叉指的是两个染色体以某种方式相互交换某些基因以形成一个新个体的过程。交叉操作后产生新的一代,继承了父代的基本特征。三交换启发式交叉算子算法的思想是在三个亲本个体间产生一个后代。与传统的只有双亲的方法相比,提出的该方法增加了产生子代染色体的信息。亲本染色体的增多提高了继承双亲优良性状的可能性,加快了算法的搜索速度。三个交换启发式交叉算子方法的图示如图5所示。

图5 带5个基因的三交叉遗传算法
Fig.5 Three-exchange heuristic crossoveroperator method with 5 genes.
以一项涉及10个工作站和5台AGV任务为例,对三交叉遗传算法详细过程如下
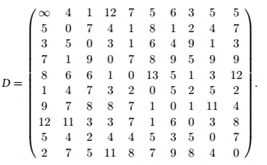
十个工作站间的距离如表1所示。
表1 10个工作站间的距离表
Tab.1 The distance between the tenworkstations.

随机选取三个个体进行交叉操作:
A = 6 2 12 7 111 8 10 3 4 13 5 9
B = 3 2 12 7 911 1 4 13 5 10 6 8
C = 5 3 10 8 711 2 6 12 1 4 13 9
路径A的总距离为81,单个AGV路径的最大距离为27.
路径B的总距离为78,单个AGV路径的最大距离为24.
路径C的总距离为71,单个AGV路径的最大距离为22.
以染色体A为参考,6是染色体的第一个位置,从右到左,循环移动染色体B和C中的基因,当6处于第一个位置时停止,然后选择6作为后代的第一点,结果如下
A= 6 2 12 7 11 1 8 10 3 4 13 5 9
B= 6 8 3 2 12 7 9 11 1 4 13 5 10
C= 6 12 1 4 13 9 5 3 10 8 7 11 2
S= 6 * * * * * * * * * * * *
从表1中,我们可以得到相应距离,d(6,2)=8,d(6,8)=11,d(6,12)=d(6,0)=9.因此有d(6,8)>d(6,12)>d(6,2).
为了满足单AGV路径距离最小化的约束条件,我们选择2作为第二点,结果如下
A = 6 2 12 7 11 1 8 10 3 4 13 5 9
B = 6 2 12 7 9 11 1 4 13 5 10 8 3
C = 6 2 12 1 4 13 9 5 3 10 8 7 11
同样,我们可以确定的交叉后代把其他基因。利用单AGV路径距离最小化约束,第一交叉步的交叉后代为S = 6 2 12 7 9 11 1 4 13 5 10 8 3
上面得到的后代染色体表明所有AGV路径总距离为65,最大路径距离单AGV是17。显然,得到的S所有AGV路径总距离和最大单AGV路径距离比原来的A,B,和C都小。
3.6 变异操作
突变是指相同的染色体内的基因交换,从而产生新的个体。变异可以保证遗传算法的局部搜索能力,保持群体的多样性,防止遗传算法过早收敛。论文中采用交换变异方法,其思想是选择有序的数a,b,c(a 例如,如果序列号a=2,b=5和C=10是随机生成的,相应的个体转换如下所示: A= 6 2 12 7 11 1 8 10 3 4 13 5 9 变异后: A= 6 1 8 10 3 4 2 12 7 11 13 5 9 假设一个有10个工作站和5台AGV的生产线。图6显示了一条随机染色体A,5个AGV各自的路径分别为 0—6—2—0 0—7—0 0—1—8—0 0—3—4—0 0—5—9—0 建立10*10的工作站距离矩阵D 具体解码步骤如下: (1)获得AGV的可达距离矩阵 将AGV1的运动路径与矩阵D比对,值1代表AGV1通过工作站,其他情况用0表示。可得到AGV1的可达矩阵X1: 同样,可以得到其他的AGV可达矩阵X2,X3,X4,X5。 (1)得到AGV路径的距离矩阵 如AGV1路径的距离矩阵为 (1)计算出AGV的路径距离 AGV1的路径距离为Z1=6+3+8=17,同样地,Z2=3+12,Z3=4+4+5=13,Z4=12+7+8=27, Z5=5+5+2=12,还有全AGV的总路径距离Z=Z1+Z2+Z3+Z4+Z5=84 a.AGV路径图 b.遗传算法迭代图 图6.AGV路径图和新的遗传算法 Fig.6 AGV diagram and map of the newgenetic algorithm. 在仿真中,假设一个5台 AGV和50个工作站的生产场景,并满足在第2节列出的要求和双路径约束条件。设置种群大小为200,应用所提出的新遗传算法进行路径优化。两种遗传算法的仿真结果如图3-6所示。图3和图4表明,在3000次迭代中,新遗传算法的总路径距离为72,传统遗传算法的路径距离为86。图表明,在60次迭代中,传统遗传算法的最大AGV距离为34,新遗传算法的最大距离为32。图10显示了这两种算法使用条形图之间的距离比较。从仿真中,我们可以得到: (1)改进的遗传算法与传统遗传算法相比,总路径距离更短。 (2)改进遗传算法收敛速度比传统遗传算法快。 图7 AGV路径图和传统遗传算法 Fig .7 AGV diagram and map of thetraditional genetic algorithm. 图8 最大单AGV距离 Fig. 8 Maximumdistance of single AGV. 图9 两种算法路程比较 Fig . 9 Distancecomparison between two algorithms. 通过将多AGV路径规划问题放到遗传算法的框架中来研究该进遗传算法在多AGV路径优化中的应用。在改进的遗传算法中,采用三交换启发交叉算子比传统两交换启发交叉算子具有更多信息,得到更加优良的后代。通过对总路径距离及各自AGV距离最小的双路径约束,在AGV输送任务中得到一个优化的最短路径总距离。仿真结果表明,采用改进的遗传算法缩短了AGV的路径距离和最短的单路径距离。 [1]Hu XS, Jiang JC, Egardt B, Cao DP. Advanced power-source integration in hybridelectric vehicles: multicriteria optimization approach. IEEE Transactions onIndustrial Electronics. 2015; 62(12), 7847–7858. [2]Hu XS, Moura Scott J, Nilolce M, Egardt B, Cao DP. Integrated optimization ofbattery sizing, charging, andpower management in plug-in hybrid electric vehicles. IEEE Transactions onControl Systems Technology.2012; 24(3), 1036–1043. [3]Hu XS, Zou Y, Yang YL. Greener plug-in hybrid electric vehicles incorporatingrenewable energy and rapidsystem optimization. Energy. 2016; 111(20): 971–980. [4]Hu XS, Clara MM, Yang YL. Charging, power management, and battery degradationmitigation in plugin hybrid electric vehicles: a unified cost-optimal approach.Mechanical Systems and Signal Processing.2017; 87(17), 4–16. [5]Zhang Z, Zhao DB, Gao JW, Wang DQ, Dai YJ. FMRQ-a multiagent reinforcementlearning algorithm for fully cooperative tasks. IEEE Transactions onCybernetics. 2017; 47(6): 1367–1379. [6]Anvari B, Angeloudis P, Ochieng WY. A multi-objective GA-based optimisation forholistic manufacturing, transportation and assembly of precast construction.Automation in Construction. 2016; 71(2):226–241. [7]Hadas Y, Nahum OE. Urban bus network of priority lanes: A combinedmulti-objective, multi-criteria and group decision-making approach. TransportPolicy. 2016; 52: 186–196. [8]Sabar NR, Kieu LM, Chung E, Tsubota T, de Almeida PEM. A memetic algorithm forreal world multiintersection traffic signal optimisation problems. EngineeringApplications of Artificial Intelligence. 2017;63: 45–53. [9]Xu G, Liang X, Yao S, Chen D, Li Z. Multi-objective aerodynamic optimization ofthe streamlined shape of high-speed trains based on the Kriging model. PLoSOne. 2017; 12(1): e0170803. [10]ChodrowPS, al-Awwad Z, Jiang S, Gonza´lez MC. Demand and congestion in multiplextransportation networks. PLoS One. 2016; 11(9): e0161738. [11]RamezaniM, Bashiri M, Tavakkoli-Moghaddam R. A new multi-objective stochastic model fora forward/reverse logistic network design with responsiveness and qualitylevel. Applied Mathematical Modelling. 2013; 37(1-2): 328–344. [12]Wang F, Lai XF, Shi N. A multi-objective optimization for green supply chainnetwork design, Decision Support Systems. 2011; 51(2): 262–269.3.7 矩阵解码


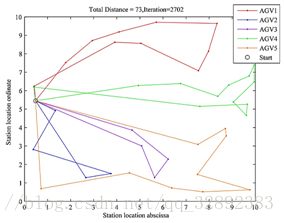
4 模拟仿真
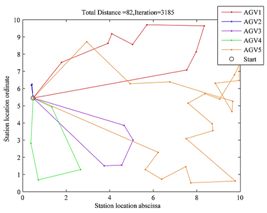
a.AGV路径图
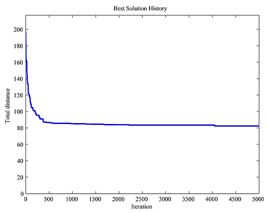
b.遗传算法迭代图
5 结论
参考文献: