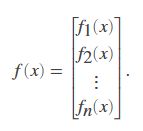MATLAB文档 lsqnonlin 函数 翻译

lsqnonlin 函数：解决非线性最小二乘问题

1. 函数句法

x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options)
x = lsqnonlin(problem)
[x,resnorm] = lsqnonlin(___)
[x,resnorm,residual,exitflag,output] = lsqnonlin(___)
[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(___)

2. 函数描述

非线性最小二乘法
解决非线性最小二乘形式的曲线拟合问题，解x具有可选的下限lb和上限ub

x, lb 和 ub 可以是矢量或矩阵。
lsqnonlin不用计算f(x) 2范数的平方，而是需要用户定义函数来计算矢量值函数

3. 输入参数

3.1 fun

fun为函数句柄或函数名，求其平方和的最小值。功能，其总和的平方被最小化，指定为功能句柄或函数名。fun接受一个数组x，返回数组F，于x评估目标函数。该函数fun可以被指定为一个文件中的函数句柄：

x = lsqnonlin(@myfun,x0)

其中myfun 是一个MATLAB函数，形如：

function F = myfun(x)
F = ...            % Compute function values at x

fun也可以是匿名函数的函数句柄

x = lsqnonlin(@(x)sin(x.*x),x0);

如果用户定义的x和F是数组，将被转换为带线性索引的矢量。

注意：
平方和不应该明确形成。相反，你的函数应该返回函数值的向量。

如果雅可比矩阵可以计算，并且雅可比的选项是“开”，设置为

options = optimoptions('lsqnonlin','SpecifyObjectiveGradient',true)

则函数fun必须返回第二输出参数，即在x处的雅可比矩阵J的值。
通过检查nargout的值，当fun被调用且仅具有一个输出参数（在优化算法只需要F，但不J的值的情况下）时，该函数可避免计算J。

function [F,J] = myfun(x)
F = ...          % Objective function values at x
if nargout > 1   % Two output arguments
   J = ...   % Jacobian of the function evaluated at x
end

如果fun返回m个分量的数组，并且x具有n个元素，其中n是x0的元素数，雅可比J是一个m*n矩阵，其中J（i，j）为F关于x（j）的偏导数。（雅可比J是F梯度的转置。）

3.2 x0

x0为初始点，为实向量或实数组。求解器使用x0元素的数量和x0的大小来确定fun接受变量的数量和大小。

3.3 lb

lb为下界，为实向量或实数组。如果x0元素的数目等于lb元素的数量，那么对于所有的i，有

x(i) >= lb(i) 

如果x0元素的数目大于lb元素的数量，那么对于1 <= i <= numel(lb)，有

x(i) >= lb(i)

如果x0元素的数目小于lb元素的数量，解算器发出警告。

3.4 ub

lb为上界。具体解释与 3.3 lb 类似。

3.5 options

优化选项，为optimoptions的输出或optimset返回的结构体。
一些选项适用于所有的算法，其他选项与特定算法相关。
有些选项是optimoptions不显示的。这些选项在以下表中用斜体字表示。

3.5.1 All Algorithms 适用于所有算法的选项

Algorithm 算法

有“信任区域反射” trust-region-reflective（默认）和“列文伯格 - 马夸尔特” levenberg-marquardt 两个选择。
该算法选项的指定有使用偏好。这只是一个偏好，因为某些条件必须满足使用的每个算法。对于信任区域反射算法，方程式的非线性系统不能被欠定，即方程的数目（通过fun返回的F的元素数）必须至少达到x的长度。列文伯格 - 马夸特算法不处理边界约束。

CheckGradients 梯度检查

比较用户提供的导数（目标或约束的梯度）和有限差分导数。选项是假（默认）或真。
对于optimset，名字是DerivativeCheck，值是“on”或“off”。

Diagnostics 诊断

显示关于函数最小化或解决的诊断信息。选项为“off”（默认）或“on”。

DiffMaxChange 最大差分变化量

有限差分梯度的最大变化量（正标量）。默认值为0。

DiffMinChange 最小差分变化量

有限差分梯度的最小变化量（正标量）。默认值为0。

Display 显示

显示级别：

1. ’off' 或 ‘none’ ：不显示输出
2. ‘iter’ ：在每次迭代中显示输出，并给出了默认退出消息。
3. ‘iter-detailed’ ：在每次迭代中显示输出，并给出了技术退出消息
4. ‘final’ (默认) ：只显示最终输出，并给出了默认退出消息
5. ‘final-detailed’：只显示最终输出，并给出了技术退出消息

FiniteDifferenceStepSize 有限差分步长

有限差分的标量或向量步长因子。当设置FiniteDifferenceStepSize为向量v时，正向有限差增量是

delta = v.*sign′(x).*max(abs(x),TypicalX)， 当 sign′(x) = sign(x) except sign′(0) = 1

中心有限差分为

delta = v.*max(abs(x),TypicalX)

标量FiniteDifferenceStepSize扩展为矢量。前向有限差​​的默认值为sqrt(eps)，中心有限差分的默认值为eps^(1/3) 。
对于optimset，名字是FinDiffRelStep。

FiniteDifferenceType 有限差分类型

有限差分，用来估计梯度，要么是 ‘forward’ （默认），或 ‘central’（中心）。 'central'需要两倍多的函数评价，更准确。
估计这两种类型的有限差分时，该算法应注意遵守边界。因此，例如，它可能需要一个反向的差分，而不是正向的，以避免在一个点的边界外评估。
对于optimset，名字是FinDiffType。

FunctionTolerance 函数公差

函数值上的终止公差是正标量。默认值为1e-6。
对于optimset，名字是TolFun。

FunValCheck 函数值检查

检查函数值是否有效。’on’ 在函数返回值为complex、Inf或NaN时显示错误。默认 ‘off’ 不显示错误。

MaxFunctionEvaluations 函数评价最大值

允许的函数计算的最大数，是一个正整数，默认值是100* numberOfVariables。
对于optimset，名字是MaxFunEvals。

MaxIterations 最大迭代次数

允许的最大迭代次数，一个正整数，默认值是400。
对于optimset，名字是MAXITER。

OptimalityTolerance 最优公差

一阶最优终止公差（正标量），默认值为1e-6。
在内部，'levenberg-marquardt' 算法采用1e-4倍的FunctionTolerance作为最优公差（停止准则），并且不使用OptimalityTolerance。
对于optimset，名字是TolFun。

OutputFcn 输出函数

指定一个或多个用户定义的函数，在每次迭代优化函数调用。传递一个函数手柄或手柄功能的单元数组。默认值值是无（[]）。

PlotFcn 绘图函数

从预定义的绘制函数或自己编写中选择，绘制算法执行过程中的各项度量。传递名字，函数句柄，或单元数组的名或函数句柄。对于自定义绘制功能，传递函数句柄。默认值是无（[]）：
'optimplotx' 绘制当前点。
'optimplotfunccount' 绘制函数计数。
'optimplotfval' 绘制函数值。
'optimplotresnorm' 绘制残差的范数。
'optimplotstepsize' 绘制步长。
'optimplotfirstorderopt' 绘制一阶最优度量。
对于optimset，名字是PlotFcns。

SpecifyObjectiveGradient 指定目标梯度

如果为假（默认值），求解器使用有限差分近似雅可比矩阵。如果为是，对目标函数，求解器使用一个用户定义的雅可比（在fun定义），或雅可比信息（使用JacobMult时）。
对于optimset，名字是Jacobian，值为'on' 或 'off'。

StepTolerance 终止公差

对x的终止公差，正标量。默认值为1e-6。
对于optimset，名字是TolX。

TypicalX 典型x值

典型的x值。TypicalX中元素的数目等于起始点x0中元素的数目。默认值是ones(numberofvariables,1)。解算器的用TypicalX来为梯度估计缩放有限差分。

UseParallel 使用并行计算

When true, the solver estimates gradients in parallel. Disable by setting to the default, false. See Parallel Computing.
为真时，求解器用并行方式估计梯度。通过设置为默认值false，可以禁用。

3.5.2 Trust-Region-Reflective Algorithm 适用于Trust-Region-Reflective Algorithm算法的选项

JacobianMultiplyFcn 雅可比相乘函数

雅可比相乘函数，指定为函数句柄。对于大规模的结构问题，这个函数无需实际构成J，计算雅可比矩阵乘积 J*Y, J'*Y, or J'*(J*Y) 。
当Jinfo 包含用于计算J*Y (或 J'*Y, 或 J'*(J*Y)) 的矩阵时，函数的形式为W = jmfun(Jinfo,Y,flag)
第一个参数Jinfo必须与由目标函数fun返回的第二个参数相同，例如，[F,Jinfo] = fun(x)。

Y是具有和J相同的行数，因为在矩阵相乘时有维数要求。flag 确定用何种乘积来计算：
如果flag=0，则W = J'*(J*Y)。
如果flag>0，则W = J*Y。
如果flag<0，则W = J'*Y。
在每种情况下，J没有明确地形成。该解算器使用Jinfo计算预条件。

注意：
'SpecifyObjectiveGradient' 必须设置为真，使求解器将Jinfo从fun传递到jmfun。
对于optimset, 名字是JacobMult。

JacobPattern 雅可比矩阵模式

用雅可比稀疏矩阵计算有限差分。当fun(i) 取决于 x(j)，设置JacobPattern(i,j) = 1；否则，设置JacobPattern(i,j) = 0.换句话说，当 ∂fun(i)/∂x(j) ≠ 0时，JacobPattern(i,j) = 1。

当不方便计算fun中的雅可比矩阵J时，使用JacobPattern，但你可以决定（比如，通过检查）什么时候fun(i) 取决于 x(j)。当你给出JacobPattern时，求解器可以通过稀疏有限差分近似J。

如果结构是未知的，不要设置JacobPattern。默认JacobPattern是一个密集的矩阵。然后求解器计算在每个迭代时计算一个完整的有限差分近似。这对于大的问题是昂贵的，所以它用来确定稀疏结构通常效果更好。

MaxPCGIter 预条件共轭梯度迭代最大值

PCG（预条件共轭梯度）迭代的最大值，正标量。默认值是max(1,numberOfVariables/2)。

PrecondBandWidth 预处理器的上限带宽

PCG预处理器的上限带宽，一个非负整数。默认PrecondBandWidth是Inf，这意味着使用直接分解（Cholesky）而不是使用共轭梯度（CG）。直接因式分解在计算上比CG更昂贵，但对解产生质量更好的步长。设置PrecondBandWidth为0对对角线预处理（上限带宽为0）。对于一些问题，中间带宽减少了PCG迭代次数。

SubproblemAlgorithm 子问题算法

确定迭代步长是如何计算的。默认值，'factorization'，花费的时间比'cg'慢但更准确的步长。

TolPCG PCG终止公差

在PCG迭代的终止公差，正标量。默认值是0.1。

3.5.3 Levenberg-Marquardt Algorithm 适用于Levenberg-Marquardt Algorithm算法的选项

InitDamping 初始值

列文伯格 - 马夸尔特参数的初始值，正标量。默认值为1e-2。

ScaleProblem 规模问题

'jacobian' 有时可以改善一个小规模问题的收敛性;默认值为'none'。

3.6 problem

问题结构，指定为具有以下字段的结构：

Field Name	Entry
objective	目标函数
x0	x的初始值
lb	下限向量
ub	上限向量
solver	‘lsqnonlin’
options	optimoptions创建的选项

在问题结构中，你必须至少提供objective, x0, solver, and options字段。
获得问题结构的最简单的方法是从优化应用程序导出问题。

4. 输出参数

4.1 x

解，返回实向量或者实数组。 x的大小是与x0的大小相同。通常，当exitflag为正时，x是问题的局部解。

4.2 renorm

残差的平方范数，返回非负实数。'resnorm'是残差在x的平方2-范数： sum(fun(x).^2)。

4.3 residual

解的目标函数的值，返回一个数组。一般情况下，residual = fun(x)。

4.4 exitflag

求解器退出的原因，返回一个整数。

值	退出原因
1	函数收敛至一个解x
2	x的变化量小于规定公差
3	残差的变化量小于规定公差
4	搜索方向的幅度小于规定公差
0	迭代次数超出options.MaxIterations 或函数评估次数超出options.MaxFunctionEvaluations
-1	输出函数终止算法
-2	问题不可行：边界 lb 和 ub 不一致

4.5 output

关于优化过程的信息，返回含字段的结构：

字段	具体意义
firstorderopt	一阶最优度量
iterations	迭代次数
funcCount	函数评估次数
cgiterations	PCG迭代的次数 (仅适用于trust-region-reflective算法)
stepsize	x的最终位移
algorithm	使用的算法
message	退出消息

4.6 lambda

解的拉格朗日乘数，返回含字段的结构：

字段	具体意义
lower	下限 lb
upper	上限 ub

4.7 jacobian

解的雅可比矩阵，返回作为一个实矩阵。jacobian(i,j) 是在解x处fun(i) 关于 x(j) 的偏微分。

5. 限制

1. Levenberg-Marquardt算法不处理边界约束。

2. trust-region-reflective 算法不能解决欠定系统。它要求方程的数量，即F的行数，大于等于变量的数量。在未确定的情况下，lsqnonlin使用Levenberg-Marquardt算法。
   综上，有边界约束的欠定系统问题，不能通过lsqnonlin解决。

3. lsqnonlin 可以用Levenberg-Marquardt算法直接求解复值的问题。然而，这种算法不接受约束的限制。为具有结合 约束的复杂问题，将变量分割为实部和虚部，再使用trust-region-reflective算法。

4. 计算预处理器之前，预处理器的计算使用了部分trust-region-reflective的方法的J'J（其中J是雅可比矩阵）的预条件共轭梯度。因此，J的一排有许多非零项，导致相当密集的乘积J'J，可能会对大问题产生昂贵的解决过程。

5. 如果x的元素没有上（或下）限，lsqnonlin更喜欢将ub（或Ib）的相应元素设置为inf（或-inf），而不是任意的非常大的正（或负）数。

在解决中小规模的问题时，你可以使用在lsqnonlin，lsqcurvefit和fsolve中的trust-region reflective算法，不用计算fun中的雅可比矩阵或提供雅可比稀疏模式。（这也适用于使用fmincon或fminunc而不计算Hessian或供给的Hessian稀疏图案。）多小才能叫小中规模？没有绝对的答案，因为它依赖于你的计算机系统配置的虚拟内存。

假设你的问题有m个方程和n个未知数。如果命令J = sparse(ones(m,n))导致你的机器上出现内存不足错误，那么这是肯定过大的问题。如果没有在一个错误发生，问题仍然可能过大。你只能通过运行它，看看MATLAB运行时系统上虚拟内存可用的总量。