PAXOS 算法 - 学习笔记

基本介绍

PAXOS 可以用来解决分布式环境下，选举（或设置）某一个值的问题。
分布式系统中有多个节点就会存在节点间通信的问题，存在着两种节点通讯模型：共享内存（Shared memory）、消息传递（Messages passing），Paxos是基于消息传递的通讯模型的。
它的假设前提是，在分布式系统中进程之间的通信会出现丢失、延迟、重复等现象，但不会出现传错的现象(假设没有拜占庭将军问题)。
Paxos算法就是为了保证在这样的系统中进程间基于消息传递就某个值达成一致。

场景介绍

比如下面的情况：有三个服务器进程 A、B、C 运行在三台主机上提供数据库服务，当一个 client 连接到任何一台服务器上的时候，都能通过该服务器进行 read 和 update 的操作。首先先看一个 A、B、C不那么均等的方法：

A、B、C选举主机名最大的服务器为 master 提供服务，所有的 read、update 操作都发生在它上面，其余的两台服务器只是 slave，当 client 是连接在 master 的服务器的时候，其直接和 master 交互，就类似于单机的场景。当 client 时连接在 slave 的时候，所有的请求被转移到了 master 上进行操作，然后再结果返回给
client。如果 master 挂了，那么剩余两台主机在检测到 master 挂的情况后，再根据主机名最大的方法选举master。

上面的算法有一个问题，它让 A、B、C不那么均等了，A、B、C存在角色之分，且在某个时候 master 挂机后，需要立刻选举出新的 master 提供服务。同时，这个算法还要求各个服务器之间保持心跳。
而 PAXOS 算法则不同，PAXOS 提供了一种将 A、B、C 等价的方式提供上面的操作，并保证数据的正确性。
在某台主机宕机后，只要总数一半以上的服务器还存活，则整个集群依然能对外提供服务，甚至不需要心跳。

算法原理

名词解释

角色分为 Proposers，Acceptors，和 Learners（允许身兼数职）

Proposers 提出提案，提案信息包括 提案编号 和 提议的 value
Acceptor 收到提案后可以接受（accept）提案，若提案获得多数 Acceptors 的接受，则称该提案被批准（chosen）
Learners 只能 “学习” 被批准的提案

划分角色后，就可以更精确的定义问题：

决议（value）只有在被 Proposers 提出后才能被批准（未经批准的决议称为“提案（proposal）”）
在一次 Paxos 算法的执行实例中，只批准（chosen）一个 value
Learners 只能获得被批准（chosen）的 value

处理流程

批准 value 的过程中，首先 Proposers 将 value 发送给 Acceptors，之后 Acceptors 对 value 进行接受（accept）。为了满足只批准一个 value 的约束，要求经“多数派（majority）”接受的 value 成为正式的决议（称为“批准”决议）。这是因为无论是按照人数还是按照权重划分，两组“多数派”至少有一个公共 Acceptor，如果每个 Acceptor 只能接受一个 value，约束 2 就能保证。

整个过程分为两个阶段：

Phase1（准备阶段）
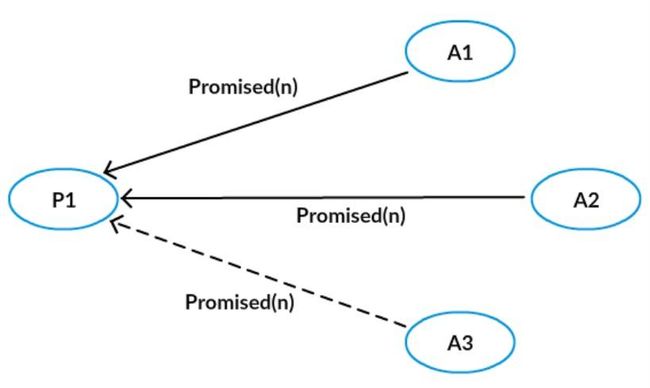
- Proposer 向超过半数（n/2+1）Acceptor 发起 prepare 消息（发送编号）
  
  image
- Acceptor 检查 prepare 消息是否符合规则（即提议编号 n 比之前接收的 prepare 请求都要大），消息符合则回复 promise 消息（并且带上之前 accept 的提议中编号小于 n 的最大的提议），否则拒绝
  
  image
Phase2（决议阶段或投票阶段）
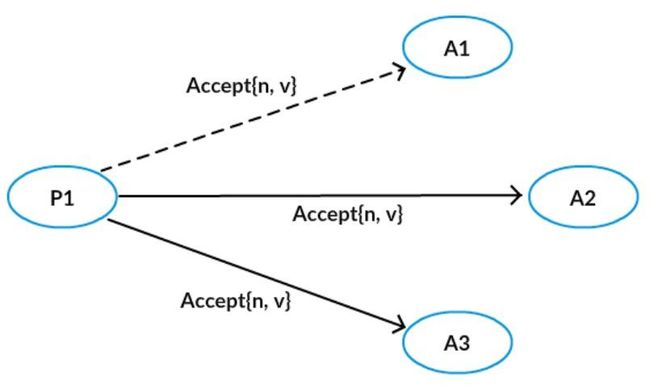
- 如果超过半数 Acceptor 回复 promise，如果没有发现有一个 Acceptor 接受过一个值，那么向所有的 Acceptor 发起自己的值和提议编号 n，否则，从所有接受过的值中选择对应的提议编号最大的，作为提议的值，提议编号仍然为 n。
  
  image
- Acceptor 检查 accept 消息是否符合规则，消息符合则批准 accept 请求
  
  image

需要注意的是，Proposer 发出 prepare（n）请求后，得到多数派的应答，然后可以随便再选择一个多数派广播 Accept 请求，而不一定要将 Accept 请求发给有应答的 Acceptor，这是常见的 Paxos 理解误区。

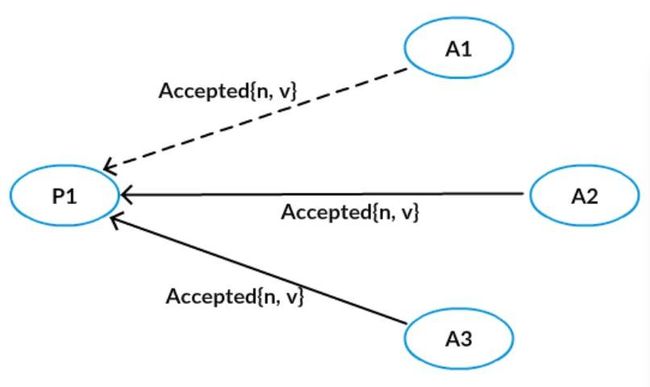
上面的图例中，P1 广播了 prepare请求，但是给 A3 的丢失，不过 A1、A2 成功返回了，即该 prepare 请求得到多数派的应答，然后它可以广播 accept 请求，但是给 A1 的丢了，不过 A2、A3 成功接受了这个提议。因为这个提议被多数派（A2、A3形成多数派）接受，我们称被多数派接受的提议对应的值被 chosen。

三个 Acceptor 之前都没有接受过 accept 请求，所以不用返回接受过的提议，但是如果接受过提议，则根据第一阶段 B，要带上之前 accept 的提议中编号小于 n 的最大的提议。

image

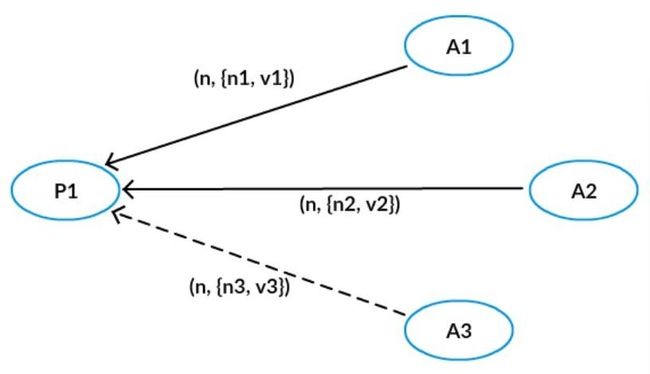
Proposer 广播 prepare 请求之后，收到了 A1 和 A2 的应答，应答中携带了它们之前接受过的 {n1, v1} 和 {n2, v2}，Proposer 则根据 n1，n2 的大小关系，选择较大的那个提议对应的值，比如 n1 > n2，那么就选择 v1 作为提议的值，最后它向 Acceptor广播提议 {n, v1}。

约束条件

P1： Acceptor 必须接受他接收到的第一个提案

注意 P1 是不完备的。如果恰好一半 Acceptor 接受的提案具有 value A，另一半接受的提案具有 value B，那么就无法形成多数派，无法批准任何一个 value。

P2：当且仅当 Acceptor 没有回应过编号大于 n 的 prepare 请求时，Acceptor 接受（accept）编号为 n 的提案

如果一个没有 chosen 过任何 Proposer 提案的 Acceptor 在 prepare 过程中回答了一个 proposer 针对提案 n的问题，但是在开始对 n 进行投票前，又接受（accept）了编号小于 n 的另一个提案（例如n-1），如果 n-1 和 n 具有不同的 value，这个投票就会违背 P2c。因此在 prepare 过程中，Acceptor 进行的回答同时也应包含承诺：不会再接受（accept）编号小于n的提案。

P3：只有 Acceptor 没有接受过提案 Proposer 才能采用自己的 value，否者 Proposer 的 value 提案为Acceptor 中编号最大的 Proposer value
P4: 一个提案被选中需要过半数的 Acceptor 接受

假设 A 为整个 Acceptor 集合，B 为一个超过 A 一半的 Acceptor 集合，B 为 A 的子集，C 也是一个超过 A 一半的 Acceptor 集合，C 也是 A 的子集，有此可知任意两个过半集合中必定有一个共同的成员 Acceptor；此说明了一个 Acceptor 可以接受不止一个提案，此时需要一个编号来标识每一个提案，提案的格式为：[编号，value]，编号为不可重复全序的，因为存在着一个一个 Paxos 过程只能批准一个 value 这时又推出了一个约束P3；

P5：当编号 K0、value为 V0 的提案(即[K0,V0])被过半的 Acceptor 接受后，今后所有比 K0 更高编号且被Acceptor 接受的提案，其 value 值也必须为 V0。

该约束还可以表述为：

一旦一个具有 value v 的提案被批准（chosen），那么之后任何 Acceptor 再次接受（accept）的提案必须具有 value v。
一旦一个具有 value v 的提案被批准（chosen），那么以后任何 Proposer 提出的提案必须具有 value v。
如果一个编号为 n 的提案具有 value v，那么存在一个多数派，要么他们中所有人都没有接受（accept）编号小于 n 的任何提案，要么他们已经接受（accept）的所有编号小于 n 的提案中编号最大的那个提案具有
value v。

因为每个 Proposer 都可提出多个议案，每个议案最初都有一个不同的 value 所以要满足 P3 就又要推出一个新的约束 P4。

决议的发布

一个显而易见的方法是当 Acceptors 批准一个 value 时，将这个消息发送给所有 Learner。但是这个方法会导致消息量过大。

由于假设没有 Byzantine failures，Learners 可以通过别的 Learners 获取已经通过的决议。因此 Acceptors 只需将批准的消息发送给指定的某一个 Learners，其他 Learners 向它询问已经通过的决议。这个方法降低了消息量，但是指定 Learners 失效将引起系统失效。

因此 Acceptors 需要将 accept 消息发送给 Learners 的一个子集，然后由这些 Learners 去通知所有 Learners 。

但是由于消息传递的不确定性，可能会没有任何 Learner 获得了决议批准的消息。当 Learners 需要了解决议通过情况时，可以让一个 Proposer 重新进行一次提案。注意一个 Learner 可能兼任 Proposer。

示例

参见 Paxos算法

引用：
分布式一致性算法Paxos介绍
Paxos算法
微信PaxosStore：深入浅出Paxos算法协议