基于注意力机制的STGCN——交通流量预测(AAAI)
Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting
摘要
预测交通流量对于交通领域的研究者来说是一个非常关键的问题。但是,由于交通流是非常复杂的,且是极度非线性的,因此这是一个非常有挑战性的任务。许多现存的交通流量预测方法,缺少对交通数据的动态时空相关性建模的能力,因此无法得到令人满意的预测结果。在这篇论文里,我们提出了一个基于注意力机制的STGCN模型去解决交通流量预测问题。ASTGCN模型包含三个相关部分各自对交通流的三大时间属性进行建模——最近、日、周,具体来说,每一个组件包含两个主要部分:
1)时空注意力机制能够有效的捕获交通数据里的动态时空相关性;
2)时空卷积的作用:用图卷积捕获空间模式;用通用标准卷积描述时间特征;
对三个组件的输出进行加权融合,得到最后的预测结果。通过真实数据PeMS进行实验,我们所提出的模型具有非常好的效果。
介绍
最近,许多国家致力于发展ITS来解决交通管理问题。交通预测是ITS不可或缺的一部分,尤其是交通流量大、交通速度快的高速公路。由于高速公路是封闭的,一旦拥挤出现,它将严重影响交通。交通流量能够有效的反应高速公路的交通状态。如果它可以提前被准确的预测,根据这个,交通管理人员将能够更合理的指挥车辆去增强高速路网的运行效率。
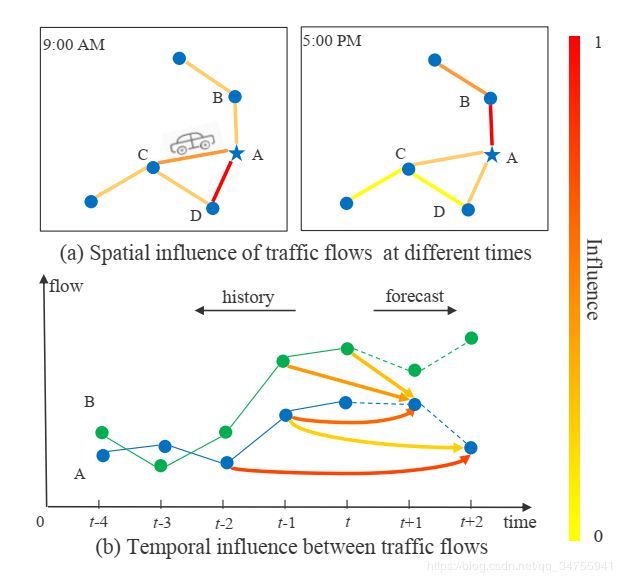
高速公路交通流预测是一个典型的时空数据预测问题。显然,在相邻位置相邻时间的观测不是独立的而是动态相关的。因此,解决这些问题的关键是能够有效的提取数据的时空相关性。图1表明了交通流的时空相关性,两点之间线的粗细表示他们的相互影响强度。线的颜色越深,影响越大。在空间维度上(如图1(a))我们可以发现不同的位置对A有不同的影响,甚至是同一个位置在不同的时间段也有不同的影响。在时间维度上(如图1(b)),不同位置的历史观测值对未来不同时期的A有不同的影响。综上所述,高速公路上交通数据在时间和空间温度上都表现出很强的动态相关性。怎样探索非线性且复杂的时空数据,发现其固有的时空模式,准确预测交通流是一个非常具有挑战性的课题。
幸运的是,随着交通运输业的发展,摄像头、传感器和其他检测器被部署在高速公路上。每一个传感器被放置在一个独特的位置上,不断生成有关交通的时间序列数据。这些设备产生了大量的带有地理信息的交通数据,为交通预测提供了坚实的数据基础。许多研究者已经为解决这些问题付出了很大的努力。早期,交通预测问题采用时间序列分析模型。然而,在实际中,对于不稳定的、非线性的数据,处理它们是非常困难的。后来,传统的机器学习方法对复杂的数据进行建模,但是它们仍然很难同时考虑高维交通数据的时空相关性。此外,这些方法的预测性能严重依赖于特征工程,这往往需要大量相关领域的专家。在最近几年里,许多研究者使用深度学习方法去处理高维时空数据,CNN能够有效的处理网格数据,GCN被用来描述图数据的相关性。但是,这些方法没能同时对交通数据的空间特征和动态相关性进行建模。
为了应对这些挑战,我们提出了一个新颖的深度学习模型:ASTGCN,去预测交通网络中每个位置的交通流。这个模型可以直接处理交通数据,并且能够有效的处理动态时空特征。本文的主要贡献如下:
1)我们开发了一个时空注意力机制去学习交通数据的动态时空相关性。具体来说,空间注意力机制被用来对不同位置的空间相关性进行建模。时间注意力机制被用来捕获不同时刻的动态时间相关性;
2)设计了一个新颖的时空卷积模块,用于对交通数据的时空相关性进行建模。它包含图卷积(能够从原始图交通网络结构中捕获空间特征);
3)在真实的公路交通数据集上进行了大量的实验,验证了我们的模型与现有的基本模型相比有更好的预测效果。
相关工作
交通预测
经过多年的不断研究和实践,关于交通预测的研究取得了许多成果。被用来进行交通预测的统计模型包括:HA,ARIMA,VAR等等。这些方法都需要数据满足一些假设,但是交通数据太复杂了无法满足这些假设,因此预测性能较差。如KNN、SVM等机器学习方法可以对更复杂的数据建模,但是却需要非常详细的特征工程。由于深度学习在语音识别、图像处理等领域的突破,越来越多的研究者将深度学习用于时空数据预测。2018年Zhang设计了一个ST-ResNet模块去预测人流量;2018年Yao提出了一个方法去预测交通(通过融合CNN和LSTM同时对时间和空间进行建模);Yao进一步提出了时空动态网络去预测出租车需求量(可以动态的学习到位置间的相似性)。尽管交通数据的时空特征可以从这些模型中提取出来,他们的限制是输入必须是标准的2D和3D网格数据。
图卷积
传统的卷积可以有效的提取数据的局部模式,但只能应用于标准网格数据。最近,图卷积将传统的卷积推广到图结构的数据。图卷积的两个主流方法是空间方法和谱方法。空间方法直接对图的节点及其相邻节点执行卷积滤波器。因此,这种方法的核心是选择节点的邻域。某某人提出了一种启发式的线性方法去选择每一个节点的邻域,这在社交网络任务里获得了很好的结果。Li将图卷积引入动作识别任务里。几种不同的策略被提出用来将每个节点的邻域划分为不同的子集,保证每个节点的子集数目相同。谱方法,在这种方法里图卷积的局域性是通过谱分析来考虑的。一个通用的图卷积网络由Bruna提出,然后其他人通过切比雪夫不等式进行了优化。某某某提出了一个门控图卷积网络去进行交通预测,但是该模型没有考虑交通数据的动态时空相关性。
注意力机制
最近,注意力机制已经在各大领域得到了广泛的应用。注意力机制的目标是从所有输入中选择相对重要的信息。Xu在图像描述任务中提出了两个注意力机制,采用一个可视化的方法去展示注意力机制的影响。对于图中的点分类任务中,Welickovic利用自注意力层去处理图结构的数据(通过神经网络),获得了不错的效果;为了预测时间序列,Liang提出了一个多层注意力机制去自适应性的调整多个传感器时间序列之间的相关性;然而,这在实践中是非常耗时的,因为需要对每个时间序列训练一个单独的模型。
基于上述研究,考虑到交通网络的图结构和交通数据的动态时空模式,我们同时采用图卷积和注意力机制去对网络结构形式的交通数据进行建模。
前期准备
交通网络
在本研究中,我们定义了一个交通网络作为一个无向图 G = ( V , E , A ) G=(V,E,A) G=(V,E,A),如图2(a),图中:V是一系列点的集合(|V|=N,点的个数);E是一系列边的集合,代表点之间的连接性; A ∈ R N ∗ N A\in R^{N*N} A∈RN∗N是图G的邻接矩阵。在交通网络G中的每一个点能够规律性的得到F个特征。换句话说,每一个点能够生成一个特征向量F,如下图:
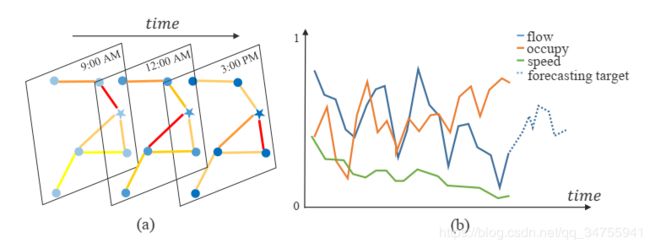
交通流预测
假设网络G中的每一个节点第f个时间序列是交通流序列,我们使用 x t c , i x_t^{c,i} xtc,i代表时刻t节点i的第c个特征, x t i x_t^i xti代表时刻t节点i的特征, X t = ( x t 1 , x t 2 , . . . , x t N ) T ∈ R N ∗ F X_t=(x_t^1,x_t^2,...,x_t^N)^T\in R^{N*F} Xt=(xt1,xt2,...,xtN)T∈RN∗F代表时刻t的所有点的所有特征。 X = ( X 1 , X 2 , . . . , X t ) T ∈ R N ∗ F ∗ t X=(X_1,X_2,...,X_t)^T\in R^{N*F*t} X=(X1,X2,...,Xt)T∈RN∗F∗t代表时间段t的所有点的所有特征。此外,我们用 y t i = x t f , i y_t^i=x_t^{f,i} yti=xtf,i代表未来时刻t节点i的交通流。
问题:给定 X X X,预测未来的时间序列 Y = ( y 1 , y 2 , . . . , y N ) T ∈ R N ∗ T p , y i = ( y t + 1 i , y t + 2 i , . . . , y t + N ) Y=(y^1,y^2,...,y^N)^T\in R^{N*T_p},y^i=(y_{t+1}^i,y_{t+2}^i,...,y_{t+N}) Y=(y1,y2,...,yN)T∈RN∗Tp,yi=(yt+1i,yt+2i,...,yt+N)
基于注意力机制的时空图卷积网络
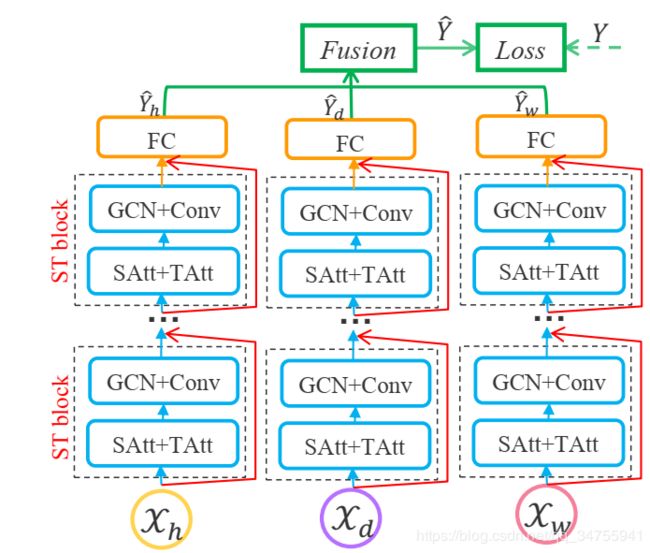
图3给出了本文提出的ASTGCN的总体框架,它包含三个主要的部分,这三大部分有着相同的结构,分别被设计用来对最近、日、周进行建模。
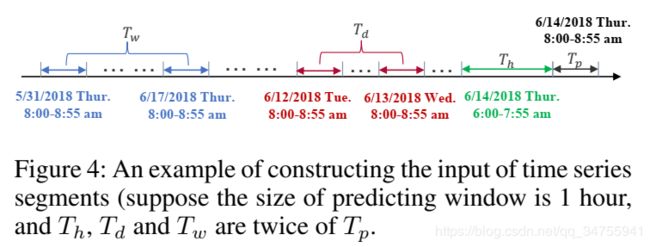
假设采样间隔是每天q次。如果当前时刻是 t 0 t_0 t0,预测窗口的大小是 T p T_p Tp,如下图所示,我们沿着时间轴截取长度为 T h T_h Th、 T d T_d Td、 T w T_w Tw,分别作为近期、日、周的输入,在这里, T h T_h Th、 T d T_d Td、 T w T_w Tw都是 T p T_p Tp的整数倍。这三个时间序列的细节如下:
(1)最近:
X h = ( X t 0 − T h + 1 , X t 0 − T h + 2 , X t 0 ) ∈ R N ∗ F ∗ T h X_h=(X_{t_0-T_h+1},X_{t_0-T_h+2},X_{t_0})\in R^{N*F*T_h} Xh=(Xt0−Th+1,Xt0−Th+2,Xt0)∈RN∗F∗Th,这是与预测周期直接相邻得到 一段时间序列,如下图的绿色部分所示。从直观上看,交通拥堵的形成和扩散是渐进的,因此,刚刚过去的交通流必然会对未来的交通流产生影响。
(2)日:
X d = ( X t 0 − ( T d / T p ) ∗ q + 1 , . . . , X t 0 − ( T d / T p ) ∗ q + T p , X t 0 − ( T d / T p − 1 ) ∗ q + 1 , . . . , X t 0 − ( T d / T p − 1 ) ∗ q + T p , . . . , X t 0 − q + 1 , . . . , X t 0 − q + T p ) ∈ R N ∗ F ∗ T d X_d=(X_{t_0-(T_d/T_p)*q+1},...,X_{t_0-(T_d/T_p)*q+T_p},X_{t_0-(T_d/T_p-1)*q+1},...,X_{t_0-(T_d/T_p-1)*q+T_p},...,X_{t_0-q+1},...,X_{t_0-q+T_p})\in R^{N*F*T_d} Xd=(Xt0−(Td/Tp)∗q+1,...,Xt0−(Td/Tp)∗q+Tp,Xt0−(Td/Tp−1)∗q+1,...,Xt0−(Td/Tp−1)∗q+Tp,...,Xt0−q+1,...,Xt0−q+Tp)∈RN∗F∗Td,包括与预测时期相同时间段的过去几天的片段,如下图的红色部分所示。由于人们的日常生活较为桂林路,交通数据会呈现重复的模式,比如每天早上的高峰期,日周期组件的目的是对交通数据的日周期性进行建模。
(3)周:
X w = ( X t 0 − 7 ∗ ( T w / T p ) ∗ q + 1 , . . . , X t 0 − 7 ∗ ( T w / T p ) ∗ q + T p , X t 0 − 7 ∗ ( T w / T p − 1 ) ∗ q + 1 , . . . , X t 0 − 7 ∗ ( T w / T p − 1 ) ∗ q + T p , . . . , X t 0 − 7 ∗ q + 1 , . . . , X t 0 − 7 ∗ q + T p ) ∈ R N ∗ F ∗ T w X_w=(X_{t_0-7*(T_w/T_p)*q+1},...,X_{t_0-7*(T_w/T_p)*q+T_p},X_{t_0-7*(T_w/T_p-1)*q+1},...,X_{t_0-7*(T_w/T_p-1)*q+T_p},...,X_{t_0-7*q+1},...,X_{t_0-7*q+T_p})\in R^{N*F*T_w} Xw=(Xt0−7∗(Tw/Tp)∗q+1,...,Xt0−7∗(Tw/Tp)∗q+Tp,Xt0−7∗(Tw/Tp−1)∗q+1,...,Xt0−7∗(Tw/Tp−1)∗q+Tp,...,Xt0−7∗q+1,...,Xt0−7∗q+Tp)∈RN∗F∗Tw,由前几周的片段组成,它们有相同的周期属性,时间片段作为预测片段。如下图的蓝色部分所示。通常,周一的交通模式和历史上周一的交通模式有一定的相似性,但可能与周末的交通模式有很大的不同。因此,设计了周周期组件来捕获流量数据中的周周期特性。
这三个组件有着相同的网络结构,他们中的每一个都包含了几个ST-Block和一个全连接层,在每一个ST-Block里,都包含了一个时空注意力模块和一个时空卷积模块。为了优化训练效率,我们采用了一个残差学习框架。最后,根据参数矩阵进一步合并三个分量的输出,得到最终的预测结果。整个网络结构被精心设计用来描述交通流的动态时空相关性。
Spatial-Temporal Attention
一个新颖的时空注意力机制被提出用来捕获动态空间和时间的相关性,它包含两种注意力机制:时间注意力机制和空间注意力机制。
Spatial attention (空间注意力)
在空间维度上,不同位置的交通状况互相影响,具有很强的动态性。在这里,我们使用一个注意力机制(Feng,2017)去自适应的调整空间维度上节点之间的动态相关性。
最近组件的注意力机制如下所示:
S = V s ∗ σ ( ( X h r − 1 W 1 ) W 2 ( W 3 X h r − 1 ) T + b s ) S=V_s*\sigma((X_h^{r-1}W_1)W_2(W_3X_h^{r-1})^T+b_s) S=Vs∗σ((Xhr−1W1)W2(W3Xhr−1)T+bs)
S i , j ′ = S i , j ∑ j = 1 N e x p ( S i , j ) S_{i,j}'=\frac{S_{i,j}}{\sum_{j=1}^Nexp(S_{i,j})} Si,j′=∑j=1Nexp(Si,j)Si,j
上式中 X h r − 1 = ( X 1 , X 2 , . . . , X T r − 1 ) ∈ R N ∗ C r − 1 ∗ T r − 1 X_h^{r-1}=(X_1,X_2,...,X_{T_{r-1}})\in R^{N*C_{r-1}*T_{r-1}} Xhr−1=(X1,X2,...,XTr−1)∈RN∗Cr−1∗Tr−1是第r层ST-Block的输入, C r − 1 C_{r-1} Cr−1是第r层输入数据的通道(即特征数),当r=1是, C 0 = F C_0=F C0=F。 T r − 1 T_{r-1} Tr−1是第r层时间维度的长度。当r=1时,在最近组件里, T 0 = T h T_0=T_h T0=Th。 V s , b s ∈ R N ∗ N , W 1 ∈ R T r − 1 , W 2 ∈ R C r − 1 ∗ T r − 1 , W 3 ∈ R C r − 1 V_s,b_s\in R^{N*N},W_1\in R^{T_{r-1}},W_2\in R^{C_{r-1}*T_{r-1}},W_3\in R^{C_{r-1}} Vs,bs∈RN∗N,W1∈RTr−1,W2∈RCr−1∗Tr−1,W3∈RCr−1都是被学习的参数,注意矩阵S是由当前的输入计算出来的。在S中 S i , j S_{i,j} Si,j 的值代表着点i和点j的相关性,然后用一个softmax激活函数确保和为1。在执行图卷积的时候,我们会将邻接矩阵A与空间注意矩阵 S i , j ′ ∈ R N ∗ N S_{i,j}'\in R^{N*N} Si,j′∈RN∗N一起使用去动态的调整两点之间的权重值。
Temporal attention (时间注意力)
在时间维度上,不同的时间间隔里交通状态之间也存在着相关性,这些相关性在不同的地点之间是动态变化的。因此,我们使用一个注意力机制去自适应性调整对数据各个时候的重视程度:
E = V e ∗ σ ( ( X h r − 1 U 1 ) U 2 ( U 3 X h r − 1 ) T + b e ) E=V_e*\sigma((X_h^{r-1}U_1)U_2(U_3X_h^{r-1})^T+b_e) E=Ve∗σ((Xhr−1U1)U2(U3Xhr−1)T+be)
E i , j ′ = E i , j ∑ j = 1 N e x p ( E i , j ) E_{i,j}'=\frac{E_{i,j}}{\sum_{j=1}^Nexp(E_{i,j})} Ei,j′=∑j=1Nexp(Ei,j)Ei,j
上式中 V e , b e ∈ R T r − 1 ∗ T r − 1 , U 1 ∈ R N , U 2 ∈ R C r − 1 ∗ N , W 3 ∈ R C r − 1 V_e,b_e\in R^{T_{r-1}*T_{r-1}},U_1\in R^{N},U_2\in R^{C_{r-1}*N},W_3\in R^{C_{r-1}} Ve,be∈RTr−1∗Tr−1,U1∈RN,U2∈RCr−1∗N,W3∈RCr−1都是被学习的参数。我们直接将归一化的时间注意力矩阵应用到输入并得到 X ^ h r − 1 = ( X ^ 1 , X ^ 2 , . . . , X ^ T r − 1 ) = ( X 1 , X 2 , . . . , X T r − 1 ) E ′ ∈ R N ∗ C r − 1 ∗ T r − 1 \hat{X}_h^{r-1}=(\hat{X}_1,\hat{X}_2,...,\hat{X}_{T_{r-1}})=(X_1,X_2,...,X_{T_{r-1}})E'\in R^{N*C_{r-1}*T_{r-1}} X^hr−1=(X^1,X^2,...,X^Tr−1)=(X1,X2,...,XTr−1)E′∈RN∗Cr−1∗Tr−1,去动态的调整输入融合相关信息。
Spatial-Temporal Convolution
时空注意力模块能够使得网络自动得关注重要的信息。由注意力机制调整后的输入被送到时空卷积模块,它的结构如图5所示。本文提出的时空卷积模块由空间维度上的图卷积构成,它能够从邻近区域获取空间的相关性,并沿着时间维度进行卷积,利用邻近时间的相关性。
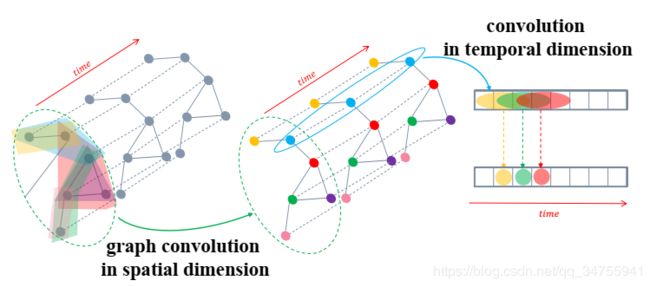
Graph convolution in spatial dimension
谱图理论将基于网格运算的卷积运算推广到图结构的数据。在这个研究里,道路网就是一个图结构的数据,每一个点的特征都可以被当做图上的一个信号。因此,为了充分利用交通网络的拓扑性,在每一个时间间隔里我们采用基于谱图理论的图卷积来直接处理信号,在空间维度上探索交通网络的信号相关性。谱图理论将一个图转换成代数形式,分析图的拓扑性(如:图结构的连通性)。
在谱图分析中,图由其对应的拉普拉斯矩阵L表示。通过分析拉普拉斯矩阵及其特征值可以得到图结构的数据。一个图的拉普拉斯矩阵被定义为L=D-A,它的正则化是 L = I N − D − 1 2 A D 1 2 ∈ R N ∗ N L=I_N-D^{-\frac{1}{2}}AD^{\frac{1}{2}}\in R^{N*N} L=IN−D−21AD21∈RN∗N, A A A是邻接矩阵(adjacent matrix), I N I_N IN是一个单位矩阵,度矩阵 D ∈ R N ∗ N D\in R^{N*N} D∈RN∗N是一个对角矩阵, D i i = ∑ j A i j D_{ii}=\sum_jA_{ij} Dii=∑jAij。拉普拉斯矩阵的特征值分解: L = U Λ U T L=U\Lambda U^T L=UΛUT,式中: Λ = d i a g ( [ λ 0 , . . . , λ N − 1 ] ) ∈ R N ∗ N \Lambda=diag([\lambda_0,...,\lambda_{N-1}])\in R^{N*N} Λ=diag([λ0,...,λN−1])∈RN∗N是一个度矩阵, U U U是傅里叶变换的基。以时刻t的交通流作为一个例子,此时在图上的信号是 x = x t f ∈ R N x=x_t^f\in R^N x=xtf∈RN,该信号的图傅里叶变换被定义为 x ^ = U T x \hat{x}=U^Tx x^=UTx,根据傅里叶变换的性质,U是一个正交矩阵,因此对应的傅里叶反变换: x = U x ^ x=U\hat{x} x=Ux^,图卷积是在傅里叶域中对角化的线性算子代替经典的卷积算子。基于此理论,在图上G的信号x被卷积核 g θ g_\theta gθ滤波:
g θ ∗ G ( x ) = g θ ( L ) x = g θ ( U Λ U T ) x = U g θ ( Λ ) U T x g_\theta *G(x)=g_\theta (L)x=g_\theta (U\Lambda U^T)x=Ug_\theta (\Lambda)U^Tx gθ∗G(x)=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx
由于图信号的卷积运算等于这些信号的乘积,这通过图傅里叶变换转换成谱域。上式可以理解为在谱域里的傅里叶变换,然后乘以变换后的结果,进行傅里叶反变换得到卷积运算的最终结果。但是,当图的尺度较大时,直接对拉普拉斯矩阵进行特征值分解代价较大,因此,本文采用切比雪夫多项式来近似的解决这一问题:
g θ ∗ G ( x ) = g θ ( L ) x = ∑ k = 0 K − 1 θ k T k ( L ^ ) x g_\theta *G(x)=g_\theta (L)x=\sum_{k=0}^{K-1}\theta_kT_k(\hat{L})x gθ∗G(x)=gθ(L)x=∑k=0K−1θkTk(L^)x
上式中: θ ∈ R K \theta \in R^K θ∈RK是一个多项式的向量, L ^ = 2 λ m a x L − I N \hat{L}=\frac{2}{\lambda_{max}}L-I_N L^=λmax2L−IN, λ m a x \lambda_{max} λmax是拉普拉斯矩阵L的最大的特征值。切比雪夫多项式的定义是: T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) , T 0 ( x ) 1 , T 1 ( x ) = x T_k(x)=2xT_{k-1}(x)-T_{k-2}(x),T_0(x)1,T_1(x)=x Tk(x)=2xTk−1(x)−Tk−2(x),T0(x)1,T1(x)=x,利用切比雪夫多项式的近似展开式来求解这一公式,提取 0 0 0到 ( K − 1 ) t h (K-1)^{th} (K−1)th阶相邻节点的信息,图卷积最终使用relu函数作为激活函数。
为了动态的调整节点之间的相关性,对于切比雪夫的每一项,我们加入空间注意力机制:
g θ ∗ G ( x ) = g θ ( L ) x = ∑ k = 0 K − 1 θ k ( T k ( L ^ ) ∗ S ′ ) x g_\theta *G(x)=g_\theta (L)x=\sum_{k=0}^{K-1}\theta_k(T_k(\hat{L})*S')x gθ∗G(x)=gθ(L)x=∑k=0K−1θk(Tk(L^)∗S′)x。
我们可以将该定义推广到多通道的图中。例如,在最近组件中,输入是 X h r − 1 = ( X 1 , X 2 , . . . , X T r − 1 ) ∈ R N ∗ C r − 1 ∗ T r − 1 X_h^{r-1}=(X_1,X_2,...,X_{T_{r-1}})\in R^{N*C_{r-1}*T_{r-1}} Xhr−1=(X1,X2,...,XTr−1)∈RN∗Cr−1∗Tr−1,每一个点的特征有 C r − 1 C_{r-1} Cr−1个通道。
Convolution in temporal dimension
在空间维度上,图卷积算子捕获到图上每一个点的邻域信息之后,在时间维度上一个标准的卷积层通过融合相邻时间片段的邻域信息去更新节点信息,如图5所示。以最近组件中的第r层的算子如下:
X h r = R e L U ( Φ ∗ ( R e L U ( g θ ∗ ( G X h r − 1 ) ) ) ∈ R C r ∗ N ∗ T r X_h^r=ReLU(\Phi*(ReLU(g_{\theta}*(_GX_h^{r-1})))\in R^{C_r*N*T_r} Xhr=ReLU(Φ∗(ReLU(gθ∗(GXhr−1)))∈RCr∗N∗Tr
上式中: ∗ * ∗是一个标准卷积核, Φ \Phi Φ是一个时间维度的卷积核参数,激活函数是 R e L U ReLU ReLU。
综上所述,时空卷积模块能够很好的捕获交通数据的时间和空间特征。时空注意模块和时空卷积模块构成了一个时空卷积块ST-Block,将多个时空块叠加,进一步提取更大范围的动态时空关联。最后,加入一个全连接层,使得各分量的输出具有与预测目标相同的尺寸和形状,并且最后的全连接层使用relu作为激活函数。
Muti-Component Fusion
在这一节中,我们将讨论怎样融合三个组件的输出。假设要预测周五上午八点的交通流量。可以看出,部分地区的交通流在上午有明显的高峰期,因此,日周期和周周期是关键的。然而,可能在一些地点,日周期和周周期没有明显的规律性的模式,因此有时候日周期和周周期可能是没有帮助的。因此,当融合不同分量的输出时,三个组件对每个节点的影响权重是不同的,需要从历史数据中学习。因此最后的预测结果如下:
Y ^ = W h ∗ Y ^ h + W d ∗ Y ^ d + W w ∗ Y ^ w \hat{Y}=W_h*\hat{Y}_h+W_d*\hat{Y}_d+W_w*\hat{Y}_w Y^=Wh∗Y^h+Wd∗Y^d+Ww∗Y^w
上式中: W h , W d , W w W_h,W_d,W_w Wh,Wd,Ww是学习参数,反应了三个时间维度分量对预测目标的影响程度。
Experiments
为了评估我们模型的性能,我们对连个真实的公路交通数据进行了比较实验。
Datasets(数据集)
我们通过加利福利亚的高速公路数据集PeMSD4和PeMSD8验证我们的模型。交通数据从原始数据中每隔5分钟汇总一次。该系统在美国各大城市里部署了39,000个检测器,检测器的地理信息被记录在数据集中,我们的实验中考虑了三种交通量,包括交通流量、平均速度、平均占有率。
PeMSD4:29条道路上部署了3848个检测器,该数据集的时间跨度为2018年1月至2月,我们选择前50天的数据作为训练集,剩下的数据作为测试集。
Preprocessing(预处理)
我们移除一些冗余的检测器,以确保相邻检测器之间的距离大于3.5英里。交通数据每5分钟汇总一次,因此每个检测器每天包含288个数据。缺失的值由线性插值补全,此外数据通过zero-mean正则化,令x的均值为0。
Settings(设置)
我们实现了基于MXnet框架的ASTGCN模块,我们令 K ∈ ( 1 , 2 , 3 ) K\in(1,2,3) K∈(1,2,3),随着K越来越大,预测性能越来越高,时间维度中的卷积大小也是如此。我们令K=3,时间维度上的卷积核大小也是3。在我们的模型中,所有的图卷积层都使用64个卷积核。所有的时间卷积层使用64卷积核,我们设置:T_h=24,T_d=12,T_w=24,预测窗口尺寸是:T_p=12,换句话说,我们的目标是预测未来一小时的交通流量。在本文中,MSE作为损失函数,通过BP网络最小化损失函数。batch_size=65,learning_rate=0.0001,此外,为了验证本文提出的时空注意力机制,我们还设计了一个弱化版本的ASTGCN,叫做MSTGCN(Muti-Component Spatial-Temporal Graph Convolution Networks),它移除了spatial-temporal attention,其他设置和ASTGCN相同。
结果比较与分析
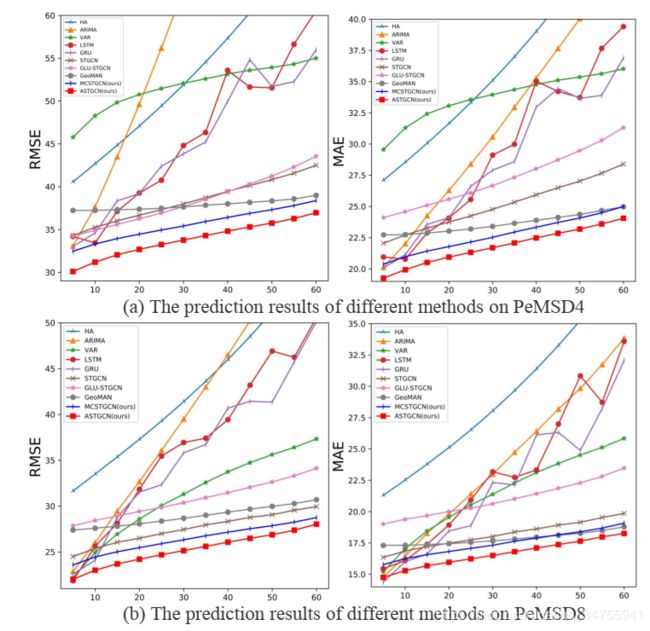
我们将我们的模型和其他8个基本模型进行了比较。表一展示了预测结果。
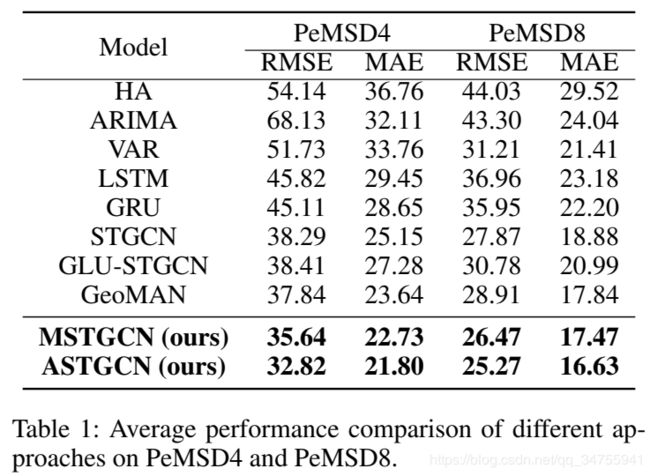
从表1可以看出,我们的ASTGCN模型在两个数据集上的评价指标都达到了最好的性能。我们可以观察到,茶峒的时间序列分析方法的预测结果往往不理想,这表明这些方法对非线性复杂交通数据建模的能力有限。通过比较可以看出,基于深度学习的方法往往能够比传统的时间序列的方法预测结果更好。其中,STGCN、GLU-STGCN、GeoMAN和我们模型的两个版本都优于传统的LSTM和GRU学习模型。并且GeoMAN的效果最好,这意味着多层注意力机制的应用,能够有效的捕获流量数据的动态变化。
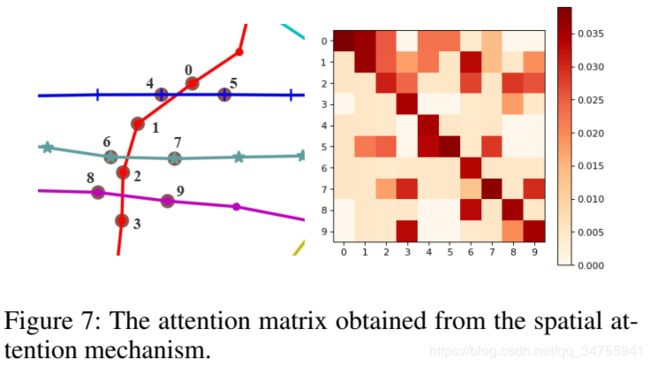
为了直观的研究注意力机制在我们的模型中的作用,我们进行了一个案例研究:从PeMSD8中选择一个带有10个检测器的子图,并且给出训练集中的空间注意矩阵。如上图所示,在空间注意矩阵里,第i行表示的是第i个探测器和其他每一个节点的相关性强弱程度。例如,看最后一行,我们可以看到第9个探测器的流量和第3个、第8个密切相关。这是非常合理的因为在真实的交通网络中,这三个检测器在空间上是相近的,如上图所示。因此,我们的模型,不仅可以获得最佳的预测性能,而且显示出可解释性的优势。
结论和未来的工作
本文提出了一种新的基于注意力机制的时空图卷积网络——ASTGCN,并成功的应用于交通流预测。该模型结合时空注意力机制和时空卷积,包括空间维度上的图卷积核时间维度上的标准卷积,同时捕获交通数据的动态时空特征。github代码地址
实际上,高速公路交通流量受到许多外部因素的影响,如天气和社会事件。未来,我们将进一步考虑外部因素,进一步提高预测精度。由于ASTGCN是一个通用的框架,我们也可以将其应用于其他实际应用,如估计到达事件。