图的五种最短路径算法
本文总结了图的几种最短路径算法的实现:深度或广度优先搜索算法,费罗伊德算法,迪杰斯特拉算法,Bellman-Ford 算法。
1)深度或广度优先搜索算法(解决单源最短路径)
从起点开始访问所有深度遍历路径或广度优先路径,则到达终点节点的路径有多条,取其中路径权值最短的一条则为最短路径。
下面是核心代码:
void dfs(int cur,int dst){
if(minpathdst){
minpath=dst;
return;
}
}
for(int i=1;i<=n;i++){
if(mark[i]==0&&edge[cur][i]!=inf&&edge[cur][i]!=0){
mark[i]=1;
dfs(i,dst+edge[cur][i]);
mark[i]=0;//需要在深度遍历返回时将访问标志置0
}
}
return;
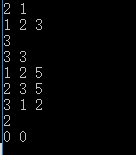
} 例:先输入n个节点,m条边,之后输入有向图的m条边,边的前两个元素表示起点和终点,第三个值表示权值,输出1号城市到n号城市的最短距离。
#include
using namespace std;
#define nmax 110
#define inf 999999999
int minpath,n,m,en,edge[nmax][nmax],mark[nmax];//最短路径,节点数,边数,终点,邻接矩阵,节点访问标记
void dfs(int cur,int dst){
if(minpathdst){
minpath=dst;
return;
}
}
for(int i=1;i<=n;i++){
if(mark[i]==0&&edge[cur][i]!=inf&&edge[cur][i]!=0){
mark[i]=1;
dfs(i,dst+edge[cur][i]);
mark[i]=0;//需要在深度遍历返回时将访问标志置0
}
}
return;
}
int main ()
{
while(cin>>n>>m&&n!=0){
//初始化邻接矩阵
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
edge[i][j]=inf;
}
edge[i][i]=0;
}
int a,b;
while(m--){
cin>>a>>b;
cin>>edge[a][b];
}
minpath=inf;
memset(mark,0,sizeof(mark));
mark[1]=1;
en=n;
dfs(1,0);
cout< 程序运行结果如下:
2)弗洛伊德算法(解决多源最短路径):时间复杂度o(n^3),空间复杂度o(n^2)
基本思想:最开始只允许经过1号顶点进行中转,接下来只允许经过1号和2号顶点进行中转.......允许经过1~n号所有顶点进行中转,来不断动态更新任意两点之间的最短距离。即求从i号顶点到j顶点只经过前k号点的最短距离。
分析如下:1,首先构建邻接矩阵edge[n+1][n+1],假如现在只允许经过1号节点,求任意两点间的最短距离,很显然edge[i][j]=min(edge[i][j],edge[i][1]+edge[1][j]),代码如下:
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(edge[i][j]>edge[i][1]+edge[1][j]){
edge[i][j]=edge[i][1]+edge[1][j];
}
}
}2.接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短距离,在已经实现了从i号顶点到j号顶点只经过前1号点的最短路程的前提下,现在插入第2号节点,来看看能不能更新最短路径,因此只需在步骤一求得的基础上,进行edge[i][j]=min(edge[i][j],edge[i][2]+edge[2][j]);.......
3.很显然,需要n次这样的更新,表示依次插入了1号2号.......n号节点,最后求得的edge[i][j]是从i号顶点到j号顶点只经过前n号点的最短路程。因此核心代码如下:
#include
using namespace std;
#define inf 999999999
int main ()
{
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(edge[k][j]edge[i][k]+edge[k][j]){
edge[i][j]=edge[i][k]+edge[k][j];
}
}
}
}
}
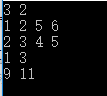
/***先输入n,m,在输入m个三元组,n为路口数,m表示有几条路,其中1为商店,n为赛场,三元组分别表示起点终点,和该路径长,输出1到n的最短距离***/
#include
using namespace std;
#define inf 999999999
#define nmax 110
int n,m,edge[nmax][nmax];
int main ()
{
int a,b;
while(cin>>n>>m&&n!=0){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
edge[i][j]=inf;
}
edge[i][i]=0;
}
while(m--){
cin>>a>>b;
cin>>edge[a][b];
edge[b][a]=edge[a][b];
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(edge[k][j]edge[i][k]+edge[k][j]){
edge[i][j]=edge[i][k]+edge[k][j];
}
}
}
}
cout< 程序运行结果如下:
3)迪杰斯特拉算法(解决单源最短路径)
基本思想:每次找到离源点(如1号节点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。
基本步骤:1,设置标记数组book[]:将所有的顶点分为两部分,已知最短路径的顶点集合P和未知最短路径的顶点集合Q,很显然最开始集合P只有源点一个顶点。book[i]为1表示在集合P中;
2,设置最短路径数组dst[]并不断更新:初始状态下,dst[i]=edge[s][i](s为源点,edge为邻接矩阵),很显然此时dst[s]=0,book[s]=1.此时,在集合Q中可选择一个离源点s最近的顶点u加入到P中。并依据以u为新的中心点,对每一条边进行松弛操作(松弛是指由顶点s-->j的途中可以经过点u,并令dst[j]=min(dst[j],dst[u]+edge[u][j])),并令book[u]=1;
3,在集合Q中再次选择一个离源点s最近的顶点v加入到P中。并依据v为新的中心点,对每一条边进行松弛操作(即dst[j]=min(dst[j],dst[v]+edge[v][j])),并令book[v]=1;
4,重复3,直至集合Q为空。
核心代码如下:
#include
using namespace std;
#define nmax 110
#define inf 999999999
/***构建所有点最短路径数组dst[],且1为源点***/
int u;/***离源点最近的点***/
int minx;
for(int i=1;i<=n;i++) dst[i]=edge[1][i];
for(int i=1;i<=n;i++) book[i]=0;
book[1]=1;
for(int i=1;i<=n-1;i++){
minx=inf;
for(int j=1;j<=n;j++){
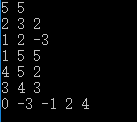
if(book[j]==0&&dst[j]dst[u]+edge[u][k]&&edge[u][k] 例1:给你n个点,m条无向边,每条边都有长度d和花费p,给你起点s,终点t,要求输出起点到终点的最短距离及其花费,如果最短距离是有多条路线,则输出花费最少的。
输入:输入n,m,点的编号是1~n,然后是m行,每行4个数a,b,d,p,表示a和b之间有一条边,且长度为d,花费为p。最后一行是两个数s,t,起点s,终点t。n和m为0时输入结束。(1 输出:输出一行,有两个数,最短距离及其花费。 分析:由于每条边有长度d和花费p,最好构建变结构体存放。 使用邻接矩阵求解: 程序运行结果如下: 4)Bellman-Ford算法(解决负权边,解决单源最短路径,前几种方法不能解决负权边) 主要思想:所有的边进行n-1轮松弛,因为在一个含有n个顶点的图中,任意两点之间的最短路径最多包含n-1条边。换句话说,第1轮在对所有的边进行松弛操作后,得到从1号顶点只能经过一条边到达其余各定点的最短路径长度,第2轮在对所有的边进行松弛操作后,得到从1号顶点只能经过两条边到达其余各定点的最短路径长度,........ 此外,Bellman-Ford算法可以检测一个图是否含有负权回路:如果经过n-1轮松弛后任然存在dst[e[i]]>dst[s[i]]+w[i]. 例1:对图中含有负权的有向图,输出从1号节点到各节点的最短距离,并判断有无负权回路。 程序运行结果如下: 5)SPFA(Shortest Path Faster Algorithm)算法是求单源最短路径的一种算法,它是Bellman-ford队列优化,它是一种十分高效的最短路算法。 实现方法:建立一个队列,初始时队列里只有起始点s,在建立一个数组记录起始点s到所有点的最短路径(初始值都要赋为极大值,该点到他本身的路径赋为0)。然后执行松弛操作,用队列里的点去刷新起始点s到所有点的距离的距离,如果刷新成功且刷新的点不在队列中,则把该点加入到队列,重复执行直到队列为空。 此外,SPFA算法可以判断图中是否有负权欢=环,即一个点的入队次数超过N。#include#include#include