RSA大数运算实现（1024位n）（4）快速求逆元算法

简介

  在前面RSA大数运算实现（1024位n）的第一篇中，求逆元的方法是使用欧几里得除法，本质上是基于除法。在第三篇中，使用Knuth的除法提高了除法的效率，即便这样，除法仍然非常耗时，其时间复杂度和乘法相当。老师提供了一种方法，如果只是单纯地求逆元，可以只基于减法和移位这样非常快的操作实现，原理也非常容易理解。
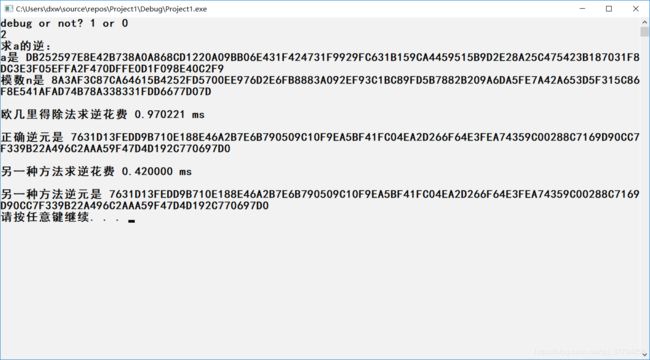
  使用这种方法求逆元，测试时，对于500多位的数字，求逆耗时大约是欧几里得除法的一半。

算法原理

给定数a和n，要求出a的逆元a^-1，使得a·a^-1=1(mod n)。
考虑方程:
    x=y·a(mod n) ①

*该方程有两个平凡解：(x₁,y₁)=(a,1)  (x₂,y₂)=(n,0)

  对于同余式，满足加法和乘法(除法)规则，以下三条规则的成立是显然的：
1. 如果(x₁,y₁)，(x₂,y₂)是方程①的解，那么，由于同余式的可加性，(x₁ - x₂,y₁ - y₂)也是方程①的一个解。
2. 如果(2·x₁,y₁)是方程①的解，那么，由于同余式的可乘性，(x₁ ,y₁/2)也是方程①的一个解。
3. 如果(1,y)是方程①的解，那么，y=a^-1

算法步骤

1. 找到方程①的两个不同的解，可以是以上的两个平凡解。
2. 如果x1是偶数且y1也是偶数，将x1和y1都右移1位；如果x1是偶数，y1不是偶数，将x1和(y1+n)右移1位。对x2和y2做同样的操作。如果在这之后，x1或者x2等于1，到第4步。
3. 做x1=x1-x2 (mod n)，y1=y1-y2(mod n)，如果在这之后，x1或者x2等于1，到第4步，否则到第2步。
4. 若x1=1，则a^-1=y1；否则a^-1=y2。

算法实现

int new_inv(BN a, BN n, BN & x)
{

	memset(x, 0, BNSIZE);
	BN   x1 = { 0 }, y1 = { 0 }, x2 = { 0 }, y2 = { 0 };
	BN temp1 = { 0 }, temp2 = { 0 };//保存中间结果


	if (cmp_b(a, ONE_BN) == 0)//如果是1,逆元就是1
	{
		SETONEBIT_B(x, 1U);
		return FLAG_OK;
	}

	gcd_b(a, n, temp1);//求公因子，判断有没有逆元
	if (cmp_b(temp1, ONE_BN) != 0)//如果不互素，没有逆元
	{
		SETZERO_B(x);
		return FLAG_NOINV;
	}

	//有逆元，就开始求。方程x=y*a (mod n)有平凡解(x1,y1)=(a,1)  (x2,y2)=(n,0)
	//初始化x1=a,y1=1  x2=n,y2=0
	cpy_b(x1, a);
	cpy_b(x2, n);
	cpy_b(y1, ONE_BN);
	cpy_b(y2, ZERO_BN);
	int i = 0;
	do
	{
		while (uint32_t(x1[1] & 1U) == 0U)//C中需要注明强制类型，否则x1[1] & 1U居然不等于0U，也不等于0,在本系统默认是0UL
		{
			shr_b(x1);
			if(uint32_t(y1[1] & 1U) == 0U)
				shr_b(y1);
			else {
				add(y1, n, y1);
				shr_b(y1);
			}
		}
		while (uint32_t(x2[1] & 1U) == 0U)
		{
			shr_b(x2);
			if (uint32_t(y2[1] & 1U) == 0U)
				shr_b(y2);
			else {
				add(y2, n, y2);
				shr_b(y2);
			}
		}
		if ((x1[0] == 1 && x1[1] == 1) || (x2[0] == 1 && x2[1] == 1))
			break;
		if (x1[0]>=x2[0] && cmp_b(x1, x2) > 0)//x1>x2时,x1=x1-x2,y1=y1-y2
		{
			sub(x1, x2, x1);
			if (y1[0] <= y2[0] && cmp_b(y1, y2) < 0)//如果y1
			{
				sub(y2, y1, temp1);
				sub(n, temp1, y1);
			}
			else {
				sub(y1, y2, y1);
			}
		}
		else//x1
		{
			sub(x2, x1, x2);
			if (y2[0] <= y1[0] && cmp_b(y2, y1) < 0)//如果y2
			{
				sub(y1, y2, temp1);
				sub(n, temp1, y2);
			}
			else {
				sub(y2, y1, y2);
			}
		}
		if ((x1[0] == 1 && x1[1] == 1) || (x2[0] == 1 && x2[1] == 1))
			break;

	} while (1);

	//初始化
	if (x1[0] == 1 && x1[1] == 1)
	{
		cpy_b(x, y1);
	}
	else {
		cpy_b(x, y2);
	}
	return FLAG_OK;
}

效果展示

对于500多位的数，该算法求逆时间大致为欧几里得算法的一半。