HNSW算法原理与源码解读
HNSW——Hierarchical NSW (分层的NSW算法),是近似k近邻搜索中的新方法,也是对NSW方法的改进,它由多层的邻近图组成,因此称为分层的NSW方法。
NSW方法
NSW的搜索机制可以通过一个例子解释清楚。

首先在这张图中有六个地点,每一个点代表一个机场,而点的大小表示了这个机场的规模。现在我们要从Toksook bay出发,目的地是Ibaza,那么首先,我们在Toksook bay附近找到了距离Ibaza最近的机场Bethel,之后,我们在Bethel附近找距离Ibaza最近的机场,最终我们找到了Anchorage,然后接着在Anchorage附近找距离Ibaza最近的机场,…,最后,我们找到了Ibaza。NSW的搜索机制就是这样的,在base node(Toksook bay)的近邻中找到与query(Ibaza)最近的点,然后把这个点更新为新的base node,再重复以上过程,直到找到query。
在上面的过程中,搜索分为两个阶段,缩小和放大阶段。我们从节点度小(机场规模小)的节点开始搜索,然后逐渐找到节点度大的节点,这是缩小阶段(粗略搜索),它能够让我们一步走很多,加快了搜索速度。找节点度大的节点的好处是它的连接数量多,能够有更多的选择,在这里,它也被称为网络中的枢纽节点。当枢纽节点与我们的query距离较近时,我们又开始搜索周围节点度小的节点,这是放大阶段(精细搜索)。缩小和放大的阶段可以理解成使用高德地图时的缩小和放大。
这样的方法高效但是也存在这问题。计算机不像人类可以选择大规模的“机场”,我们只传递给它距离信息,因此在它选择“机场“的时候,只会考虑距离因素,而不考虑”机场“的规模。假设我们从Toksook bay出发的时候,有一个距离更近的小规模机场A,那我们会去这个A机场,然后假如A机场旁边又有一个小机场B且距离最近,那我们会去这个B机场。就这样我们陷入了局部搜索而很难达到目的地。
解决这个问题的一个方法是从节点度大的节点开始搜索,实验证明这个方法能在低维数据上有较高的准确率和性能。但是,NSW方法在搜索上的时间复杂度是多重对数复杂度,而且它在高维的数据上表现不行。它具有多重对数复杂度的原因是:NSW中计算距离的次数,大致与贪婪搜索的跳数和贪婪路径上的节点度的乘积成比例。其中平均跳数是对数复杂度的,而贪婪路径上的节点度也是对数复杂度,原因有两个:
- 随着网络的生成,贪婪搜索总是倾向于走同一个枢纽节点。
- 枢纽节点的连接数与网络的大小成对数增长。
因此,HNSW方法就提出固定每个元素的连接数,这样就获得了对数复杂度。
HNSW方法
HNSW的改进方法主要有:
- 使用了分层的结构,根据特征半径分层,每一个元素的层 l = − l n ( u n i f ( 0 , 1 ) ) × m L l=-ln(unif(0,1))×m_{L} l=−ln(unif(0,1))×mL。这样看来,每个元素的层次似乎是随机的,但其实,作者在论文中提到, m L = 1 / l n ( M ) m_{L} = 1/ln(M) mL=1/ln(M) 是最佳选择(有实验数据证明),而M是每个元素的最大连接数,因此这也就保证了高层节点有较大的节点;
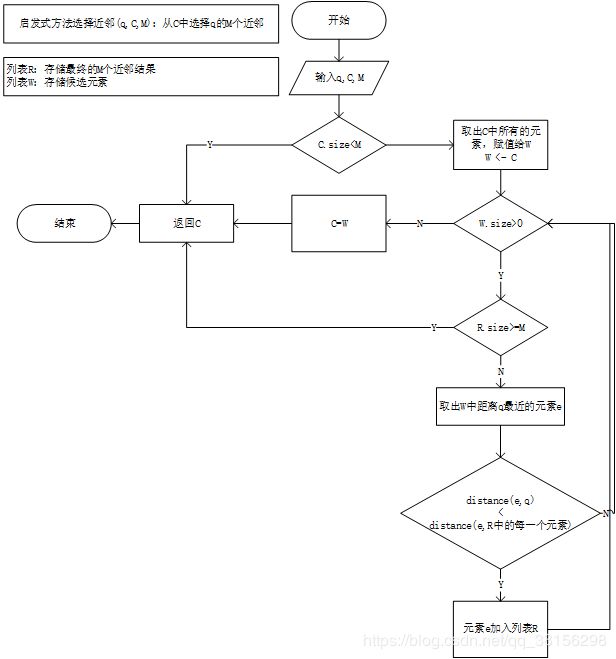
- 使用了一种启发式方法选择某节点的邻居。
这个启发式方法考虑了候选者之间的距离,对聚集起来的数据很有用。原理也用一个例子说清楚。
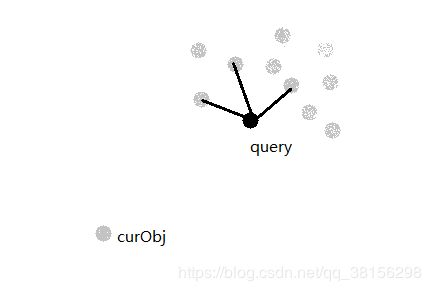
在这张图中,我们的启发式方法要在灰色的候选集中选择query的m个近邻。此时,我们已经选了query的三个近邻,在图中已经与query相连。现在,对于curObj这个点,我们是否会选择它呢?可以注意到,curObj与已经相连的三个点之间的距离 >= curObj与query的距离,因此,我们会选择curObj作为query的近邻。启发式方法只有在以下情况建立与query的连接:候选元素与任何已连接的候选元素之间的距离 >= 该候选元素与query的距离。
HNSW算法解读
这里的hnsw算法来自hnswlib。
建图流程
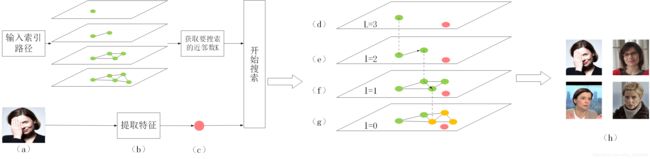
图1. HNSW算法的建图流程,其中红色节点代表待插节点,绿色表示已插入节点。(1)输入建立索引所需的参数,设M=2;(2)获取用于建图的所有图片,并依次传入算法中建立索引;(3)对输入的图片提取特征;(4)将特征当作节点,并获取节点的层次l;(5)插入节点,对于第一个插入的节点,不做任何操作。(6)① 在L层找到距离待插节点最近的节点ep,并作为下一层的输入;②该层及以下为待插元素的插入层,从ep开始查找距离待插元素最近的ef个节点,从ef节点中选出M个与待插节点连接,并将这M个节点作为下一层的输入;③从M个节点开始搜索,找到距离与待插节点最近的ef个节点,并选出M个与待插元素连接;④ 同③。(7)①在L层找到距离待插节点最近的节点ep,并作为下一层的输入;②在l=2层找到距离待插节点最近的节点ep,并作为下一层的输入;③该层及以下为待插元素的插入层,从ep开始查找距离待插元素最近的ef个节点,从ef节点中选出M个与待插节点连接,并将这M个节点作为下一层的输入;④同③。
搜索流程
图2. 检索流程,其中红色的节点表示搜索节点q(可以是非图中的节点),绿色节点表示图中已建立的节点,黄色的节点表示搜索结果。(a)输入索引路径和图片;(b)根据索引路径加载索引,并对图片提取特征;(c)获取需要搜索的近邻数K,并将图片特征作为节点输入搜索算法;(d)在L层找到距离q最近的一个节点ep,并作为下一层的输入;(e)在l=2层中,从ep开始,在ep的邻居中找到距离q最近的一个邻居,作为新的ep,并作为下一层的输入;(f)在l=1层中,从ep开始,在ep的邻居中找到距离q最近的一个邻居,作为新的ep,并作为下一层的输入;(g)在最底层中,从ep开始,搜索距离q最近的K个节点;(h)输出节点q和K个近邻。
相关算法
SEARCH-LAYER(q,ep,ef, l c l_{c} lc)
这是论文中的alg.2,寻找一层中距离q最近的ef个邻居,通过动态邻居W返回,ep是enterpoint。

// 这里是论文中的alg.2---找出layer中距离data point(也就是论文中的q)最近的前ef个元素,返回动态列表top_candidates
std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst>
searchBaseLayer(tableint enterpoint_id, void *data_point, int layer) {
// visitedList包括数组和数,visited_array 是数组,tag是数
VisitedList *vl = visited_list_pool_->getFreeVisitedList();
// visited_array存储已访问的元素
vl_type *visited_array = vl->mass;
vl_type visited_array_tag = vl->curV;
// top_candidates存储每一层距离datapoint最近的ef个邻居,对应于论文中的动态列表W
std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> top_candidates;
// candidateSet存储候选元素,对应于动态列表中的C
std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> candidateSet;
// 计算data_point(query) 到enterpoint的距离,结果保存在dist中。
dist_t dist = fstdistfunc_(data_point, getDataByInternalId(enterpoint_id), dist_func_param_);
// enterpoint加入到最近邻列表
top_candidates.emplace(dist, enterpoint_id);
// enterpoint加入到候选列表
candidateSet.emplace(-dist, enterpoint_id);
// enterpoint加入已访问列表
visited_array[enterpoint_id] = visited_array_tag;
// lowerBound存储当前到datapoint的最近距离
dist_t lowerBound = dist;
//当候选列表不为空时 while |C|>0
while (!candidateSet.empty()) {
// 从C中取出距离q最近的元素
std::pair<dist_t, tableint> curr_el_pair = candidateSet.top();
// 如果C中最近元素与q的距离 > W中与q最远元素的距离,说明W中的每一个元素都已评估过,退出循环
if ((-curr_el_pair.first) > lowerBound) {
break;
}
// 弹出候选列表队头
candidateSet.pop();
//获取当前元素的label
tableint curNodeNum = curr_el_pair.second;
std::unique_lock <std::mutex> lock(link_list_locks_[curNodeNum]);
// 获取当前元素的邻居
int *data;// = (int *)(linkList0_ + curNodeNum * size_links_per_element0_);
// 如果在第0层
if (layer == 0):
// 计算当前元素邻居的内存
data = (int *) (data_level0_memory_ + curNodeNum * size_data_per_element_ + offsetLevel0_);
else
// 计算当前元素邻居的内存
data = (int *) (linkLists_[curNodeNum] + (layer - 1) * size_links_per_element_);
// 把邻居的内存指向的数赋给size
int size = *data;
// datal表示当前元素第一个邻居的label
tableint *datal = (tableint *) (data + 1);
// 对于layer层中的当前元素的每一个邻居candidate
for (int j = 0; j < size; j++) {
tableint candidate_id = *(datal + j);
// 如果candidate已经访问过(对应论文中,如果e属于v,无操作,循环次数加1)
if (visited_array[candidate_id] == visited_array_tag) continue;
// 没有访问过,将已访问列表中并入candidate
visited_array[candidate_id] = visited_array_tag;
// 根据candidate的id号获取这个candidate元素,也就是currObj1
char *currObj1 = (getDataByInternalId(candidate_id));
//计算currObj1到data point之间的距离,对应于论文中的distance(e,q)
dist_t dist1 = fstdistfunc_(data_point, currObj1, dist_func_param_);
// 取出top_candidates中距离data point最远的元素并比较大小
// 对应于论文中,如果distance(e,q)
if (top_candidates.top().first > dist1 || top_candidates.size() < ef_construction_) {
// 将currObj1的id——candidate_id加到候选列表中
candidateSet.emplace(-dist1, candidate_id);
// 将currObj1的id——candidate_id加到动态列表中
top_candidates.emplace(dist1, candidate_id);
// 如果动态列表的长度大于ef,那么减掉“最弱的”元素,对应于论文中|W| > ef
if (top_candidates.size() > ef_construction_) {
// 取出W中距离q最远的元素
top_candidates.pop();
}
// 更新distance(f,q)
lowerBound = top_candidates.top().first;
}
}
}
visited_list_pool_->releaseVisitedList(vl);
// 返回动态列表,也就是返回layer层中距离q最近的ef个邻居
return top_candidates;
} SELECT-NEIGHBORS-HEURISTIC(q,C,M, l c l_{c} lc)
// 论文中的alg.4--启发式方法选择邻居,从top_candidates中选择距离q最近的M个元素
void getNeighborsByHeuristic2(
std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> &top_candidates,
const size_t M) {
// 如果top_candidates里元素个数小于M,那还选个啥,直接return
if (top_candidates.size() < M) {
return;
}
// queue_closest是working queue for the candidates,论文中是W ,存放候选者
std::priority_queue<std::pair<dist_t, tableint>> queue_closest;
// return_list存放最终的M个结果,论文中是R,初始为空集
std::vector<std::pair<dist_t, tableint>> return_list;
// 将queue_closest初始化为top_candidates,论文中为W<--C
while (top_candidates.size() > 0) {
queue_closest.emplace(-top_candidates.top().first, top_candidates.top().second);
top_candidates.pop();
}
// 当queue_closest内的元素个数大于0
while (queue_closest.size()) {
// 如果return_list内元素个数已经大于M,那么启发式查找过程结束
if (return_list.size() >= M)
break;
// curent_pair是queue_closest(W)的元素
std::pair<dist_t, tableint> curent_pair = queue_closest.top();
// dist_to_query是curent_pair与query的距离
dist_t dist_to_query = -curent_pair.first;
// queue_cloest元素减一
queue_closest.pop();
bool good = true;
// 对于return_list(R)中的每一个元素
for (std::pair<dist_t, tableint> second_pair : return_list) {
// curdist是 curent_pair 与 return_list(R)中的每个元素的距离
dist_t curdist =
fstdistfunc_(getDataByInternalId(second_pair.second),
getDataByInternalId(curent_pair.second),
dist_func_param_);;
// 如果curent_pair 与已经与q连接元素的距离 < curent_pair与query的距离
if (curdist < dist_to_query) {
// curent_pair将不会作为q的邻居返回
good = false;
break;
}
}
// 如果curent_pair 与已经与q连接元素的距离 >= curent_pair与query的距离,见论文中Fig.2
// 那么将curent_pair并入return_list(也就是论文里的R)
if (good) {
return_list.push_back(curent_pair);
}
}K-NN-SEARCH(q,k)
//knn搜索 ---论文中的alg.5
std::priority_queue<std::pair<dist_t, labeltype >> searchKnn(const void *query_data, size_t k) const {
// currObj和curdist分别记录距离data point最近的点和距离
tableint currObj = enterpoint_node_;
dist_t curdist = fstdistfunc_(query_data, getDataByInternalId(enterpoint_node_), dist_func_param_);
// 在层L...1之间
for (int level = maxlevel_; level > 0; level--) {
while (changed) {
// 首先没有变化,表示在同一层中搜索
changed = false;
int *data;
// 获得currObj的连接数,也就是邻居
data = (int *) (linkLists_[currObj] + (level - 1) * size_links_per_element_);
int size = *data;
tableint *datal = (tableint *) (data + 1);
// 对于currObj的每一个邻居,计算它与data point的距离,并及时更新currObj和currdist
for (int i = 0; i < size; i++) {
// 获取邻居的id
tableint cand = datal[i];
if (cand < 0 || cand > max_elements_)
throw std::runtime_error("cand error");
// 根据id获取邻居并计算其到query的距离
dist_t d = fstdistfunc_(query_data, getDataByInternalId(cand), dist_func_param_);
// 如果这个邻居与query的距离比curdist还要小,更新curdist为这个邻居,changed改为true
if (d < curdist) {
curdist = d;
currObj = cand;
changed = true;
}
}
}
}
// 目前已获得第一层与query最近的元素currObj
// 在第零层获取currObj邻居中距离query最近的max(k,ef)个近邻,也就是动态列表top_candidates-----论文中是W
std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> top_candidates = searchBaseLayerST(
currObj, query_data, std::max(ef_,k));
std::priority_queue<std::pair<dist_t, labeltype >> results;
// top_candidates修剪为k个
while (top_candidates.size() > k) {
top_candidates.pop();
}
// 结果存到result中
while (top_candidates.size() > 0) {
std::pair<dist_t, tableint> rez = top_candidates.top();
results.push(std::pair<dist_t, labeltype>(rez.first, getExternalLabel(rez.second)));
top_candidates.pop();
}
return results;
};addPoint(q,id)
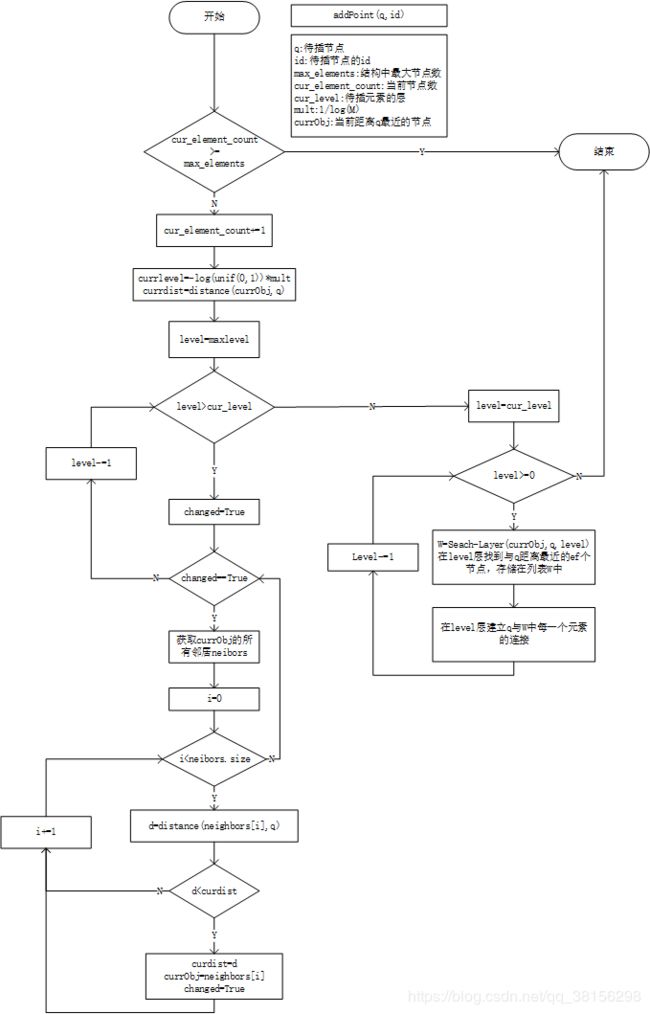
代码贴不动了 还有的代码太长,需要的同学可以私信O(∩_∩)O。
HNSW中的关键
1. 层与层之间如何建立连接?
在HNSW结构中,层与层之间并没有直接的实际连接,比如在搜索算法中,从高层到低层是通过循环完成的,在每一层中重新获得元素的邻居以实现“更新”层的操作。
2. 节点的结构是怎样的?
节点结构类似于结构体,通过pair定义,节点中包括两个属性,一是该节点与q的距离,另一个是每个节点独有的id,根据id号可以实现点与点之间的连接。例如A点有一个关于邻居的表data,其中存储了A点邻居的id,如果A点要与B点连接,只要将B点的id加到这个表中。
3. HNSW如何根据尺度半径分层?
在插入过程中,决定一个节点的层数是通过 l = − l n ( u n i f ( 0 , 1 ) ) ∗ m L l=-ln(unif(0,1))*m_{L} l=−ln(unif(0,1))∗mL,决定的,其中是0到1之间的随机数,mL是归一化因子,看起来节点层数的决定具有随机性,但其实, m L = 1 / l n ( M ) m_{L}=1/ln(M) mL=1/ln(M),M是节点的连接数。M增大, m L m_{L} mL单调递减,而 − l n ( u n i f ( 0 , 1 ) ) -ln(unif(0,1)) −ln(unif(0,1))也是单调递减的,因此随着M的增大,节点的l也会增大,也就保证了根据尺度半径分层。 这里有点问题。
4.如何获取元素的邻居?
以第一层为例,代码中定义了一个字符串数组data_level0_memory,用来保存第0层的全部内容。假设结构中一共有1000个元素,maxM=16,maxM0=32,data_size=128。那么有:
(以下部分可以对照源码理解)
size_links_level0_ = 32*4 + 4 = 132
size_data_per_element_ = size_links_level0_ + 128 + 4 = 264
(以上式子中,加4是为了获取真实的物理地址,见博客)
(以下两个变量为偏移值,待会儿解释)
offsetData_ = size_links_level0_ = 132
label_offset_ = 128 + size_links_level0_ = 260
data_level0_memory_ = (char *) malloc(max_elements_ * size_data_per_element_)
也就是说data_level0_memory_是一个1000×264的字符串数组。
这里data_level0_memory_(1000*264)的结构是这样的:

可以把一个264的大小看成是一个单位,这样的单位一共有1000个,每一个单位的结构是这样的:

这样的结构有一个好处,可以使用一个元素的id获取该元素data。例如在代码中有这样一个函数
// 根据internal_id获取元素id
inline labeltype *getExternalLabeLp(tableint internal_id) const {
return (labeltype *) (data_level0_memory_ + internal_id * size_data_per_element_ + label_offset_);
}假如我们传入的internal_id=2,那么data_level0_memory_ + 2*264 +260就指向了第二个元素中data_size后的位置,根据这个位置,可以得到元素的id(也就是label)。
// 根据internal_id获取Data
inline char *getDataByInternalId(tableint internal_id) const {
return (data_level0_memory_ + internal_id * size_data_per_element_ + offsetData_);
}同理,假如我们传入的internal_id=2,那么data_level0_memory_+2*264+132就指向了size_links_level0之后的位置,也是data的第一个位置,这样就可以获得data了。
这样看来,offsetData和label_offset_的作用就很明显了,他们分别数据data和元素id的偏移量,为了能够找到一个元素中处于不同位置的data和id。
获取邻居也是一样的道理,邻居都存储在size_links_level0这块内存中,其中一共有32个links,获取的规则和之前一样,例如:
// 获取curNodeNum的邻居id
data = (int *) (data_level0_memory_ + curNodeNum * size_data_per_element_ + offsetLevel0_);
tableint *datal = (tableint *) (data + 1);此时的datal数组中就存储了元素curNodeNum 的所有邻居id。
应用
基于HNSW近邻算法的人脸检索Web应用