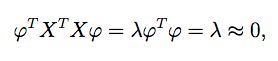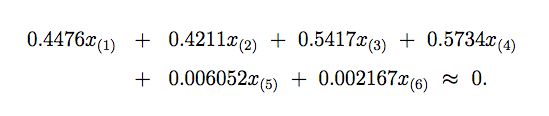各位小伙伴们劳动节快乐,利用假期的这几天的时间,在王者荣耀游戏时间之余研究了一下一直困扰我很久的多重共线性,所以今天能够用一篇文章来讲一讲我理解的多重共线性,并且希望大家可以给我多多指教,话不多说,马上开始.
有的时候,当自变量彼此相关时,回归模型可能非常令人糊涂,估计的效应会随着模型中的其他的自变量而改变数值,甚至是符号,所以我们在分析的时候,了解自变量间的关系的影响是很重要的,因此这个复杂的问题就常被称之为共线性或多重共线性.
1:什么是多重共线性?
按照定义上来说,如果存在某个常数C0,C1,C2,并且使得线性等式满足以下情况:
并且满足对于数据中的所有数据中的样本都成立,则两个自变量X1和X2位精准共线性的.
在实际的操作中,精准的共线性是很少概率发生的,因此如果上边的那个公式近似的对测量数据成立,那么就可以说他们有近似的共线性.一个常用但是不是完全适合的X1和X2间的共线性程度的度量,是他们样本系数的平方R所决定的,精准共线性对应的R=1,非共线性对应的R=0.所以因此来说,当R越来越接近于1时,近似的共线性会越来越强.通常,我们去掉形容词近似,当R较大的时候,我们就说X1和X2是共线性的.
对于P(>2)个自变量,如果存在常数C0,C1.......CP使得如下公式可以近似表示:
那么我们通常称这个P个变量存在多重共线性.
2:多重共线性的发现
将x(1),x(2),···,x(p)是自变量X1,X2,···,Xp经过中心化和标准化得到的向量,记作X=(x(1),x(2),···,x(p)),设λ为XTX的一个特征值,φ为对应的特征向量,其长度为1,即φTφ = 1.此时若λ ≈ 0,则:
用φT左乘上式,得到:
所以有Xφ ≈ 0;
即:
其中φ=(φ1,φ2,···,φp)T表明,向量x(1),x(2),···,x(p)之前有近似的线性关系,也就是说,对于自变量X1,X2,......,Xp,存在C0,C1,……,Cp之间使得
c1X1 +c2X2 +···+cpXp =c0近似成立,这就可以说明自变量之间存在有多重共线性.
度量多重共线性的严重程度的一个重要指标是方矩的XTX的条件数,即如下所示:
其中λmax(XTX),λmin(XTX)表示的是XTX的最大,最小的特征值.
直观上,条件数刻画的XTX的特征值差异的大小,从实际应用的角度,一般若K<100,则认为多重共线性的程度很小,若是100<=K<=1000,则认为存在一般程度上的多重共线性,若是K>1000,则就认为存在严重的多重共线性.
因为我最近一直在学习R语言,所以我想用个R语言的实例来更好的解释下多重共线性的问题.
例1:
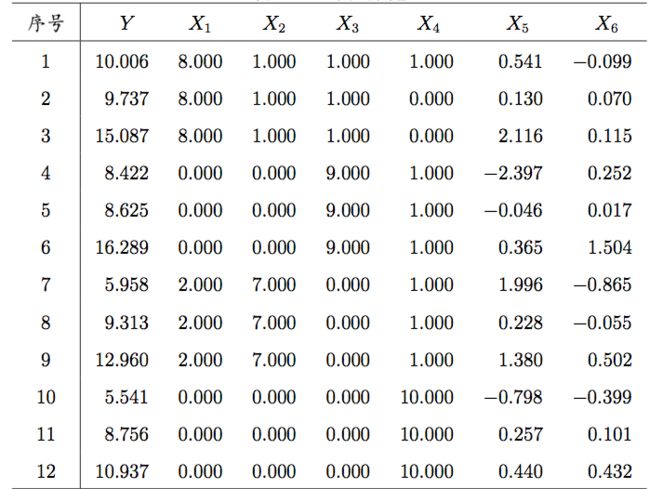
考虑一个有六个回归自变量的线性回归问题,原始数据如下图:
这里一共有12组数据,除了第一组外,自变量X1,X2....,X6的其余11组数据均满足线性关系:
X1+X2+X3+X4=10;
现在试图用求矩阵条件数的方法,来分析数自变量之间存在的多重共线性.
首先先补充一些R语言的知识,在R语言中,函数Kappa()是计算矩阵的条件数,其使用的方法为Kappa(z,exact =FALSE,…).
其中的z是矩阵,exact是逻辑变量,当exact=TRUE时,精确计算条件数,否则近似计算条件数.
现在开始解题了,首先第一步,用数据框的方法输入数据,由自变量X1,X2,......X6中心化和标准化得到的矩阵XTX本质上就是由这些自变量生成的相关矩阵,再用Kappa()函数求出矩阵的条件数,用eigen()函数求出矩阵XTX的最小特征值和相应的特征向量,求解问题的R程序如下:
得到的条件数K=2195.908>1000,这个时候我们可以认为有严重的多重共线性,进一步,我们要试图找出那些变量是多重共线性的,计算矩阵的特征值和相应的特征向量:
输入eigen(XX)
这个时候我们可以得到:
λmin = 0.001106,
φ =(0.4476,0.4211,0.5417,0.5734,0.006052,0.002167)T .
所以我们可以得到结果:
因为X(5),X(6)前边的系数近似等于0,因此我们可以得到:
所以存在着C0,C1,C2,C3,C4使得:
这样其实就可以说明变量X1,X2,X3,X4之间存在着多重共线性,这个与题目中的变量是相同的,因此我们的问题也就迎刃而解了.
所以上述就是我对于多重共线性的一些理解,但是我觉得里边还有很多知识上的漏洞需要去解决补充,也欢迎大家可以给我多多提出意见,祝大家节日快乐.