统计学习方法 第九章习题答案
文章目录
- 习题9.1
- 习题9.2
- 习题9.3
- 习题9.4
习题9.1
如例9.1的三硬币模型.假设观测数据不变,试选择不同的初值,例如 π 0 = 0.46 , p 0 = 0.55 , q 0 = 0.67 \pi^0=0.46, p^0=0.55,q^0=0.67 π0=0.46,p0=0.55,q0=0.67求模型参数 θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)的极大似然估计。
例9.1(三硬币模型)假设有3枚硬币,分别记作A,B,C.这些硬币正面出现的概率分别是π,p和q.进行如下掷硬币试验:先掷硬币A,根据其结果选出硬币B或硬币C,正面选硬币B,反面选硬币C;然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里,n=10),观测结果如下:
1,1,0,1,0,0,1,0,1,1假设只能观测到掷硬币的结果,不能观测掷硬币的过程.问如何估计三硬币正面出现的概率,即三硬币模型的参数.
解答

由公式9.5得到
μ j 1 = { 0.537 y j = 0 0.412 y j = 1 \mu^1_j=\left\{\begin{matrix} 0.537\qquad y_j=0\\0.412\qquad y_j=1 \end{matrix}\right. μj1={0.537yj=00.412yj=1
利用迭代公式9.6~9.8迭代
π 1 = 0.462 , p 1 = 0.535 , q 1 = 0.656 \pi^1=0.462,\quad p^1=0.535,\quad q^1=0.656 π1=0.462,p1=0.535,q1=0.656
同理
μ j 2 = { 0.537 y j = 0 0.412 y j = 1 \mu^2_j=\left\{\begin{matrix} 0.537\qquad y_j=0\\0.412\qquad y_j=1 \end{matrix}\right. μj2={0.537yj=00.412yj=1
π 2 = 0.462 , p 2 = 0.535 , q 2 = 0.656 \pi^2=0.462,\quad p^2=0.535,\quad q^2=0.656 π2=0.462,p2=0.535,q2=0.656
得到模型参数 θ \theta θ的极大似然估计
π ^ = 0.462 , p ^ = 0.535 , q ^ = 0.656 \hat{\pi}=0.462,\quad \hat p=0.535,\quad \hat q=0.656 π^=0.462,p^=0.535,q^=0.656
代码验证一下
import numpy as np
theta = np.array([0.46, 0.55, 0.67])
Y = np.array([1,1,0,1,0,0,1,0,1,1])
mu = np.zeros(Y.shape[0])
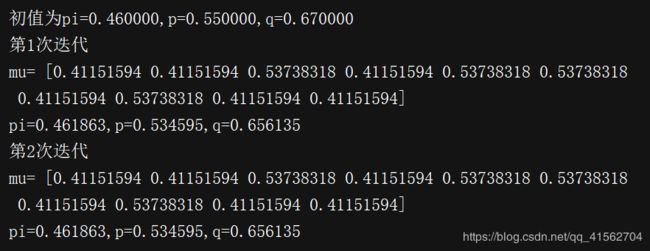
print("初值为pi=%f,p=%f,q=%f"%(theta[0], theta[1], theta[2]))
for j in range(2):
print("第%d次迭代"%(j+1))
# E step
for i in range(Y.shape[0]):
temp = theta[0]*theta[1]**Y[i]*(1-theta[1])**(1-Y[i])
temp1 = (1 - theta[0])*theta[2]**Y[i]*(1-theta[2])**(1-Y[i])
mu[i] = temp / (temp + temp1)
print("mu=",mu)
# M step
theta[0] = 1.0 / Y.shape[0] * sum(mu)
theta[1] = sum(mu * Y) / sum(mu)
theta[2] = sum((1 - mu)*Y) / sum(1-mu)
print("pi=%f,p=%f,q=%f" % (theta[0], theta[1], theta[2]))
习题9.2
证明引理9.2.
若 P ~ θ ( Z ) = P ( Z ∣ Y , θ ) \tilde P_\theta(Z) = P(Z|Y,\theta) P~θ(Z)=P(Z∣Y,θ),则 F ( P ~ , θ ) = l o g P ( Y ∣ θ ) F(\tilde P,\theta)=logP(Y|\theta) F(P~,θ)=logP(Y∣θ)
解答
F ( P ~ , θ ) = E p [ l o g P ( Y , Z ∣ θ ) ] + H ( P ~ ) = E p [ l o g P ( Y , Z ∣ θ ) ] − E P ~ l o g P ~ ( Z ) = ∑ z P ~ θ ( Z ) l o g P ( Y , Z ∣ θ ) − ∑ Z P ~ ( Z ) l o g P ~ ( Z ) = ∑ z P ( Z ∣ Y , θ ) l o g P ( Y , Z ∣ θ ) − ∑ Z P ( Z ∣ Y , θ ) l o g P ( Z ∣ Y , θ ) = ∑ z P ( Z ∣ Y , θ ) l o g P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ) = ∑ z P ( Z ∣ Y , θ ) l o g P ( Y ∣ θ ) = l o g P ( Y ∣ θ ) F(\tilde P,\theta)\\=E_p[logP(Y,Z|\theta)]+H(\tilde P)\\=E_p[logP(Y,Z|\theta)]-E_{\tilde P}log\tilde P(Z)\\=\sum_z\tilde P_\theta(Z)logP(Y,Z|\theta)-\sum_Z\tilde P(Z)log\tilde P(Z)\\=\sum_zP(Z|Y,\theta)logP(Y,Z|\theta)-\sum_ZP(Z|Y,\theta)logP(Z|Y,\theta)\\=\sum_zP(Z|Y,\theta)log\frac{P(Y,Z|\theta)}{P(Z|Y,\theta)}\\=\sum_zP(Z|Y,\theta)logP(Y|\theta)\\=logP(Y|\theta) F(P~,θ)=Ep[logP(Y,Z∣θ)]+H(P~)=Ep[logP(Y,Z∣θ)]−EP~logP~(Z)=∑zP~θ(Z)logP(Y,Z∣θ)−∑ZP~(Z)logP~(Z)=∑zP(Z∣Y,θ)logP(Y,Z∣θ)−∑ZP(Z∣Y,θ)logP(Z∣Y,θ)=∑zP(Z∣Y,θ)logP(Z∣Y,θ)P(Y,Z∣θ)=∑zP(Z∣Y,θ)logP(Y∣θ)=logP(Y∣θ)
习题9.3
已知观测数据
-67,-48,6,8,14,16,23,24,28,29,41,49,56,60,75
试估计两个分量的高斯混合模型的5个参数.

其中
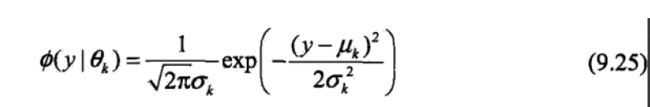
解答
先简单理一下题目的意思,这个模型由两个高斯模型混合而成,5个参数指的是两个高斯模型的参数 μ 0 , σ 0 , μ 1 , σ 1 \mu_0,\sigma_0,\mu_1,\sigma_1 μ0,σ0,μ1,σ1,另外还有其对应的系数 α 0 , α 1 ( α 0 + α 1 = 1 ) \alpha_0, \alpha_1(\alpha_0+\alpha_1=1) α0,α1(α0+α1=1),相当于只需要求一个系数。
初值设置为 σ = 1.0 , μ = 0.5 , α = 0.5 \sigma=1.0,\mu=0.5,\alpha=0.5 σ=1.0,μ=0.5,α=0.5
import numpy as np
from scipy.stats import norm
y = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28, 29, 41, 49, 56, 60, 75])
K = 2 # 两个高斯
N = 15 # y有15个数据
# 参数初始化
mu = np.array([0.5, 0.5])
sigma = np.array([1.0, 1.0]) * 10
alpha = np.array([0.5, 0.5])
for i in range(10):
gm = np.zeros((N, K))
# E 步
for j in range(N):
for k in range(K):
gm[j, k] = alpha[k] * norm(mu[k], sigma[k]).pdf(y[j]) #使用scipy实现高斯分布
gm[j, :] /= sum(gm[j, :]) # gm[j,:] = gm[j,:] /sum(gm[j,:])
# M 步
mu2 = y.dot(gm) / sum(gm)
alpha2 = sum(gm) / N
sigma2 = np.zeros((2,))
sigma2[0] = sum(gm[:, 0] * (y - mu[0]) ** 2) / sum(gm[:, 0])
sigma2[1] = sum(gm[:, 1] * (y - mu[1]) ** 2) / sum(gm[:, 1])
#判断是否收敛
if sum((mu - mu2) ** 2 + (sigma - sigma2) ** 2 + (alpha - alpha2) ** 2) < 0.01:
break
mu = mu2
sigma = sigma2
alpha = alpha2
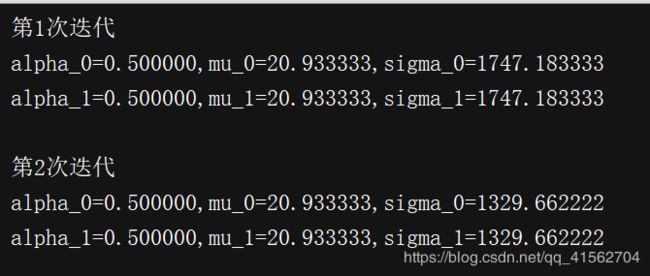
print("第%d次迭代\nalpha_0=%f,mu_0=%f,sigma_0=%f\nalpha_1=%f,mu_1=%f,sigma_1=%f\n"
%(i+1, alpha[0], mu[0], sigma[0], alpha[1], mu[1], sigma[1]))
习题9.4
EM算法可以用到朴素贝叶斯法的非监督学习.试写出其算法.
参考Blog