统计学习方法 第十一章习题答案
文章目录
- 习题11.1
- 习题 11.2
- 习题11.3
- 习题11.4
习题11.1
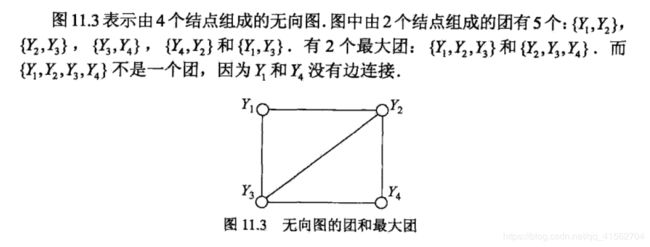
写出图11.3中无向图描述的概率图模型的因子分解式。
解答
P ( Y 1 , Y 2 , Y 3 , Y 4 ) = 1 Z ψ c 1 ( Y 1 , Y 2 , Y 3 ) ψ c 2 ( Y 2 , Y 3 , Y 4 ) P(Y_1,Y_2,Y_3,Y_4)=\frac{1}{Z} \psi_{c_1}(Y_1,Y_2,Y_3) \psi_{c_2}(Y_2,Y_3,Y_4) P(Y1,Y2,Y3,Y4)=Z1ψc1(Y1,Y2,Y3)ψc2(Y2,Y3,Y4)
Z = ∑ Y ψ c 1 ( Y 1 , Y 2 , Y 3 ) ψ c 2 ( Y 2 , Y 3 , Y 4 ) Z=\sum_Y\psi_{c_1}(Y_1,Y_2,Y_3) \psi_{c_2}(Y_2,Y_3,Y_4) Z=∑Yψc1(Y1,Y2,Y3)ψc2(Y2,Y3,Y4)
习题 11.2
证明 Z ( x ) = α n T ( x ) ⋅ 1 = 1 T ⋅ β 0 ( x ) Z(x)=\alpha_{n}^{\mathrm{T}}(x) \cdot 1=1^{\mathrm{T}} \cdot \beta_{0}(x) Z(x)=αnT(x)⋅1=1T⋅β0(x),其中1是元素均为1的m维列向量。
解答
本式子出现在书的199页11.3.1前向-后向算法这一小节
PS:书中是 β 1 ( x ) \beta_1(x) β1(x),但是我个人觉得这儿应该是 β 0 ( x ) \beta_0(x) β0(x)
Z ( x ) = ( M 1 ( x ) M 2 ( x ) . . . M n + 1 ( x ) ) s t a r t , s t o p Z(x)=(M_1(x)M_2(x)...M_{n+1}(x))_{start,stop} Z(x)=(M1(x)M2(x)...Mn+1(x))start,stop即 M 1 ( x ) M 2 ( x ) . . . M n + 1 ( x ) M_1(x)M_2(x)...M_{n+1}(x) M1(x)M2(x)...Mn+1(x)得到的结果矩阵 M M M(mm维度)的 ( s t a r t , s t o p ) (start,stop) (start,stop)位置的元素。其中 M n + 1 ( x ) M_{n+1}(x) Mn+1(x)为m*m维度的矩阵,但是只有stop列为1,其余为0。或者说 Z ( x ) Z(x) Z(x)的值为 M 1 ( x ) M 2 ( x ) . . . M n ( x ) M_1(x)M_2(x)...M_{n}(x) M1(x)M2(x)...Mn(x)结果矩阵 M ′ M' M′的start行的所有元素之和。
α n T ( x ) ⋅ 1 = α n − 1 T ( x ) M n ( x ) ⋅ 1 = α n − 2 T ( x ) M n − 1 ( x ) M n ( x ) ⋅ 1 = . . . = α 0 T ( x ) M 1 ( x ) M 2 ( x ) . . . M n ( x ) ⋅ 1 = Z ( x ) \alpha_{n}^{\mathrm{T}}(x) \cdot 1\\=\alpha_{n-1}^{\mathrm{T}}(x)M_n(x) \cdot 1\\=\alpha_{n-2}^{\mathrm{T}}(x)M_{n-1}(x)M_n(x) \cdot 1\\=...\\=\alpha^T_0(x) M_1(x)M_2(x)...M_n(x)\cdot 1\\=Z(x) αnT(x)⋅1=αn−1T(x)Mn(x)⋅1=αn−2T(x)Mn−1(x)Mn(x)⋅1=...=α0T(x)M1(x)M2(x)...Mn(x)⋅1=Z(x)
说明: α 0 T ( x ) M 1 ( x ) M 2 ( x ) . . . M n ( x ) \alpha^T_0(x) M_1(x)M_2(x)...M_n(x) α0T(x)M1(x)M2(x)...Mn(x)得到的是1m维度的行向量,其值为 M 1 ( x ) M 2 ( x ) . . . M n ( x ) M_1(x)M_2(x)...M_{n}(x) M1(x)M2(x)...Mn(x)的 s t a r t start start行的元素,将其与1是元素均为1的m维列向量点乘,得到的即为 M 1 ( x ) M 2 ( x ) . . . M n + 1 ( x ) M_1(x)M_2(x)...M_{n+1}(x) M1(x)M2(x)...Mn+1(x)的 ( s t a r t , s t o p ) (start,stop) (start,stop)位置的元素值。
1 T ⋅ β 0 ( x ) = 1 T ⋅ M 1 ( x ) β 1 ( x ) = . . . = 1 T ⋅ M 1 ( x ) M 2 ( x ) M 3 ( x ) . . . M n ( x ) ⋅ β n + 1 ( x ) = Z ( x ) 1^{\mathrm{T}} \cdot \beta_{0}(x)\\=1^T\cdot M_1(x)\beta_1(x)\\=...\\=1^T\cdot M_1(x)M_2(x)M_3(x)...M_n(x)\cdot \beta_{n+1}(x)\\=Z(x) 1T⋅β0(x)=1T⋅M1(x)β1(x)=...=1T⋅M1(x)M2(x)M3(x)...Mn(x)⋅βn+1(x)=Z(x)
说明:同理, M 1 ( x ) M 2 ( x ) M 3 ( x ) . . . M n ( x ) ⋅ β n + 1 ( x ) M_1(x)M_2(x)M_3(x)...M_n(x)\cdot \beta_{n+1}(x) M1(x)M2(x)M3(x)...Mn(x)⋅βn+1(x)得到的是列向量,其每个值为 M 1 ( x ) M 2 ( x ) . . . M n ( x ) M_1(x)M_2(x)...M_{n}(x) M1(x)M2(x)...Mn(x)的对应的一行元素之和(除了start列处,其余元素为0,与 1 T 1^T 1T点乘后得到的即为 M 1 ( x ) M 2 ( x ) . . . M n + 1 ( x ) M_1(x)M_2(x)...M_{n+1}(x) M1(x)M2(x)...Mn+1(x)的 ( s t a r t , s t o p ) (start,stop) (start,stop)位置的元素值。
习题11.3
写出条件随机场模型学习的梯度下降法.
参考Blog
习题11.4
参考图11.6的状态路径图,假设随机矩阵 M 1 ( x ) , M 2 ( x ) , M 3 ( x ) , M 4 ( x ) M_1(x),M_2(x),M_3(x),M_4(x) M1(x),M2(x),M3(x),M4(x)分别是
M 1 ( x ) = [ 0 0 0.5 0.5 ] , M 2 ( x ) = [ 0.3 0.7 0.7 0.3 ] M_{1}(x)=\left[\begin{array}{cc}0 & 0 \\ 0.5 & 0.5\end{array}\right], \quad M_{2}(x)=\left[\begin{array}{cc}0.3 & 0.7 \\ 0.7 & 0.3\end{array}\right] M1(x)=[00.500.5],M2(x)=[0.30.70.70.3]
M 3 ( x ) = [ 0.5 0.5 0.6 0.4 ] , M 4 ( x ) = [ 0 1 0 1 ] M_{3}(x)=\left[\begin{array}{cc}0.5 & 0.5 \\ 0.6 & 0.4\end{array}\right], \quad M_{4}(x)=\left[\begin{array}{cc}0 & 1 \\ 0 & 1\end{array}\right] M3(x)=[0.50.60.50.4],M4(x)=[0011]
求以start=2为起点stop=2为终点的所有路径的状态序列y的概率及概率最大的状态序列.
解答
y = ( 1 , 1 , 1 ) = a 21 b 11 c 11 = 0.5 ∗ 0.3 ∗ 0.5 = 0.075 y=(1,1,1)=a_{21}b_{11}c_{11}=0.5*0.3*0.5=0.075 y=(1,1,1)=a21b11c11=0.5∗0.3∗0.5=0.075
y = ( 1 , 1 , 2 ) = a 21 b 11 c 12 = 0.5 ∗ 0.3 ∗ 0.5 = 0.075 y=(1,1,2)=a_{21}b_{11}c_{12}=0.5*0.3*0.5=0.075 y=(1,1,2)=a21b11c12=0.5∗0.3∗0.5=0.075
y = ( 1 , 2 , 1 ) = a 21 b 12 c 21 = 0.5 ∗ 0.7 ∗ 0.6 = 0.21 y=(1,2,1)=a_{21}b_{12}c_{21}=0.5*0.7*0.6=0.21 y=(1,2,1)=a21b12c21=0.5∗0.7∗0.6=0.21(最大)
y = ( 1 , 2 , 2 ) = a 21 b 12 c 22 = 0.5 ∗ 0.7 ∗ 0.4 = 0.14 y=(1,2,2)=a_{21}b_{12}c_{22}=0.5*0.7*0.4=0.14 y=(1,2,2)=a21b12c22=0.5∗0.7∗0.4=0.14
y = ( 2 , 1 , 1 ) = a 22 b 21 c 11 = 0.5 ∗ 0.7 ∗ 0.5 = 0.175 y=(2,1,1)=a_{22}b_{21}c_{11}=0.5*0.7*0.5=0.175 y=(2,1,1)=a22b21c11=0.5∗0.7∗0.5=0.175
y = ( 2 , 1 , 2 ) = a 22 b 21 c 12 = 0.5 ∗ 0.7 ∗ 0.5 = 0.175 y=(2,1,2)=a_{22}b_{21}c_{12}=0.5*0.7*0.5=0.175 y=(2,1,2)=a22b21c12=0.5∗0.7∗0.5=0.175
y = ( 2 , 2 , 1 ) = a 22 b 22 c 21 = 0.5 ∗ 0.3 ∗ 0.6 = 0.09 y=(2,2,1)=a_{22}b_{22}c_{21}=0.5*0.3*0.6=0.09 y=(2,2,1)=a22b22c21=0.5∗0.3∗0.6=0.09
y = ( 2 , 2 , 2 ) = a 22 b 22 c 22 = 0.5 ∗ 0.3 ∗ 0.4 = 0.06 y=(2,2,2)=a_{22}b_{22}c_{22}=0.5*0.3*0.4=0.06 y=(2,2,2)=a22b22c22=0.5∗0.3∗0.4=0.06