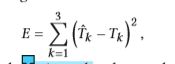学习笔记12-23
无向图与有向图的存储与操作
const int MaxSize = 10; //图中最多顶点个数
template < class T >
class MGraph
{
public:
MGraph(T a[], int n, int e); //构造函数,初始化具有n个顶点e条边的无向图
void DFST(); //深度优先遍历图
void BFST(); //广度优先遍历图
private:
void DFSTraverse(int v); //从顶点v出发深度优先遍历图
void BFSTraverse(int v); //从顶点v出发广度优先遍历图
T vertex[MaxSize]; //存放图中顶点的数组
int arc[MaxSize][MaxSize]; //存放图中边的数组
int vertexNum, arcNum; //图的顶点数和边数
};
template
void MGraph::DFST()
{
for (j = 0; j
void MGraph::BFST()
{
for (j = 0; j
struct VertexNode //定义顶点表结点
{
T vertex;
ArcNode *firstedge;
};
设计实验用邻接表类ALGraph,包括遍历操作。
const int MaxSize=10; //图的最大顶点数
template < class T >
class ALGraph
{
public:
ALGraph(T a[ ], int n, int e); //构造函数,初始化一个有n个顶点e条边的有向图
~ALGraph( ); //析构函数,释放邻接表中各边表结点的存储空间
void DFST (); //深度优先遍历图
void BFST (); //广度优先遍历图
private:
void DFSTraverse(int v); //从顶点v出发深度优先遍历图
void BFSTraverse(int v); //从顶点v出发广度优先遍历图
VertexNode adjlist[MaxSize]; //存放顶点表的数组
int vertexNum, arcNum; //图的顶点数和边数
};
深度优先搜索
template
void MGraph::DFST()
{
for (j=0; j
void MGraph::BFST()
{
for (j=0; j Deep High Dynamic Range Imaging of Dynamic Scenes
-
首先使低曝光度的图片趋近于高曝光度的图片,

-
对于低,高曝光度的图片使用calculate flow光流算法使之扭曲对其中曝光度的图片。
光流(optical flow):图片移动时每个像素的x,y位移量, -
然后对底动态图片转化为高动态图片
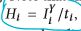
-
CIFAR10
该数据集共有60000张彩色图像,这些图像是32*32,分为10个类,每类6000张图。这里面有50000张用于训练,构成了5个训练批,每一批10000张图;另外10000用于测试,单独构成一批。测试批的数据里,取自10类中的每一类,每一类随机取1000张。抽剩下的就随机排列组成了训练批。注意一个训练批中的各类图像并不一定数量相同,总的来看训练批,每一类都有5000张图。

- 使用keras导入数据,并对数据集进行划分,然后转换数据类型防止负数自动转正,最后对数据集归一化,使之像数值处于0-1之间。
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
- 测试集与训练集初始维度维(32, 32, 3),使用mask面罩调整输入图像维数,使训练集于测试集转化为(3072)
num_training = x_train.shape[0]
mask = range(num_training)
x_train = x_train[mask]
y_train = y_train[mask]
num_test = x_test.shape[0]
mask = range(num_test)
x_test = x_test[mask]
y_test = y_test[mask]
x_train = np.reshape(x_train, (x_train.shape[0], -1))
x_test = np.reshape(x_test, (x_test.shape[0], -1))
- 实现自定义KNN算法
其方法封装为KNN,
class KNN(object):
def __init__(self, k=4):
assert k >= 1, "k must be valid!"
self.k = k
#设置训练数据
def fit(self, x_train, y_train):
assert x_train.shape[0] == y_train.shape[0], "Both of them must be equal !"
assert self.k <= x_train.shape[0], "The size of X_train must at least k."
self.X_train = x_train
self.y_train = y_train
#使用KNN计算测试数据于训练数据之间的距离
def predict(self, x):
assert self.X_train is not None and self.y_train is not None, "must fit before predict"
assert x.shapep[1] == self.X_train.shape[1], " The feature of X_predict must equal to X_train."
vote = []
for i in range(len(x)):
diffmat = x_train - x[i, :]
sqrt = diffmat**2
for j in range(3070):
sqrt[:, 0] = sqrt[:, 0]+sqrt[:, j+1]
distance = sqrt[:, 0] ** 0.5
mindistance = distance.argsort()
ClassCount = {}
for p in range(self.k):
votelabel = y_train[mindistance[p]]
ClassCount[votelabel[0]] = ClassCount.get(votelabel[0], 0)+1
vote_dic = sorted(ClassCount.items(), key=lambda m: m[1], reverse=True)
vote.append(vote_dic[0][0])
return vote
#计算精度
def accuracy(self, predict):
num_correct = 0
for i in range(len(predict_)):
if(predict_[i]==y_test[i]):
num_correct = num_correct + 1
accuracy = num_correct/len(predict_)
return accuracy
- 调试代码
if __name__ == '__main__':
knn = KNN()
knn.fit(x_train[0:10000, :], y_train[0:10000, :])
predict_ = knn.predict(x_test[0:100, :])
print(predict_)
print(y_test[0:100, :])
accuracy = knn.accuracy(predict_)
print(accuracy)