粒子群优化算法PSO

一.粒子群优化算法概念

1. 基本思想
   粒子群算法(PSO)属于群智能算法的一种，是通过模拟鸟群捕食行为设计的。假设区域里就只有一块食物（即通常优化问题中所讲的最优解），鸟群的任务是找到这个食物源。鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即我们所说的找到了最优解，即问题收敛。
2. 流程
   标准PSO的算法流程如下：
     <1>初始化一群微粒（群体规模为m），包括随机的位置和速度；
     
     <2>评价每个微粒的适应度；
     
     <3>对每个微粒，将它的适应值和它经历过的最好位置pbest的作比较，如果较好，则将其作为当前的最好位置pbest；
     
     <4>对每个微粒，将它的适应值和全局所经历最好位置gbest的作比较，如果较好，则重新设置gbest的索引号；
     
     <5>变化微粒的速度和位置；
     
     <6>如未达到结束条件（通常为足够好的适应值或达到一个预设最大代数Gmax），回到2）。

二. 代码实现及结果分析

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的三个参数
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.8   %惯性权重

maxgen=1000;   % 进化次s数  
sizepop=200;   %种群规模

Vmax=1;       %限制速度围
Vmin=-1;     
popmax=5;    %变量取值范围
popmin=-5;
dim=10;       %适应度函数维数

func=1;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(func);%画出待优化的函数，只画出二维情况作为可视化输出

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,dim);    %初始种群
    V(i,:)=Vmax*rands(1,dim);             %初始化速度
                                     %计算适应度
    fitness(i)=fun(pop(i,:),func);   %粒子的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);   %全局最佳
pbest=pop;                %个体最佳
fitnesspbest=fitness;     %个体最佳适应度值
fitnessgbest=bestfitness; %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    fprintf('第%d代，',i);
    fprintf('最优适应度%f\n',fitnessgbest);
    for j=1:sizepop
        
        %速度更新
        V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:)); %根据个体最优pbest和群体最优gbest计算下一时刻速度
        V(j,find(V(j,:)>Vmax))=Vmax;   %限制速度不能太大
        V(j,find(V(j,:)popmax))=popmax;%坐标不能超出范围
        pop(j,find(pop(j,:)0.98                         %加入变异种子，用于跳出局部最优值
            pop(j,:)=rands(1,dim);
        end
        
        %更新第j个粒子的适应度值
        fitness(j)=fun(pop(j,:),func); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnesspbest(j)
            pbest(j,:) = pop(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnessgbest
            gbest = pop(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i)=fitnessgbest;    
        
end
%% 结果分析
figure;
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

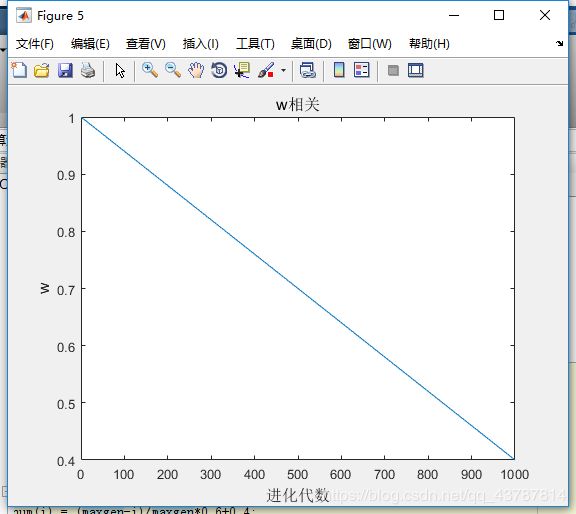
1.设定进化次数与w的线性关系如下图

<1>c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.8 %惯性权重
maxgen=1000; % 进化次s数
dim=10
sizepop=200;

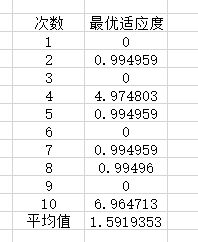
<2>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.65 %惯性权重
maxgen=500; % 进化次s数
dim=10
sizepop=200;

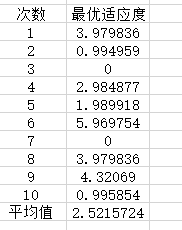
<3>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.5 %惯性权重
maxgen=800; % 进化次s数
dim=10
sizepop=200;

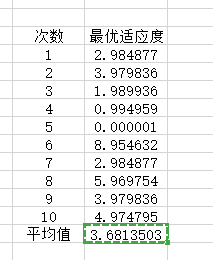
<4>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.4 %惯性权重
maxgen=1000; % 进化次s数
dim=10
sizepop=200;

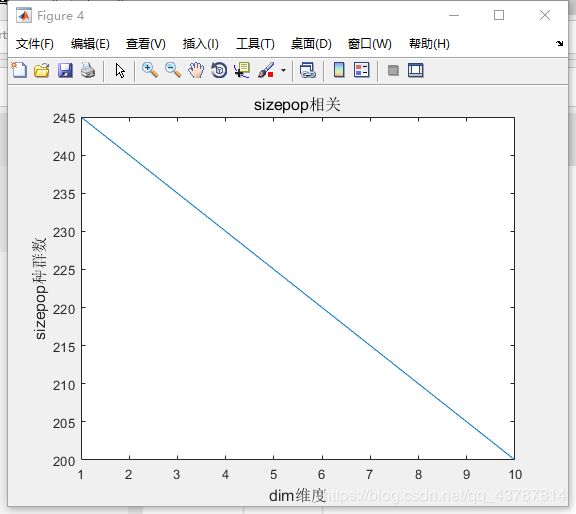
2.假定种群规模和维度线性关系如下图，进行参数变化

<1>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.4 %惯性权重
maxgen=1000; % 进化次s数
sizepop=200; %种群规模
dim=10; %适应度函数维数

<2>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.4 %惯性权重
maxgen=1000; % 进化次s数
sizepop=225; %种群规模
dim=5; %适应度函数维数

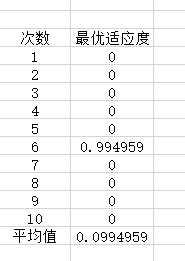
此时10组最优度测试均为0；

<3>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.4 %惯性权重
maxgen=1000; % 进化次s数
sizepop=220; %种群规模
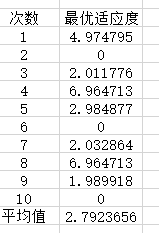
dim=9时

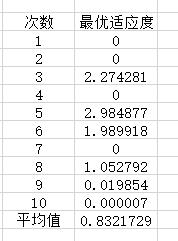
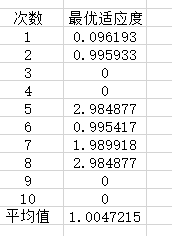
<4>
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.4 %惯性权重
maxgen=1000; % 进化次s数
sizepop=210; %种群规模
dim=8;

三.实验结论

1. 进化次数比较多时，惯性权重w越小，收敛增快，结果越优

2. 维度比较小时，即使种群规模变大，收敛速度明显增快，当维度为8时已有明显影响，结果比较好，最优适应度已几乎达优，可见维度对适应度影响还是比较快的

3. 进化次数比较多时函数更优，但是总体而言进化次数对其影响不是很大

4.维度不变时，种群规模对最优适应度影响比较小，可见种群规模并不是影响的主要因素，种群规模主要影响运行时间。