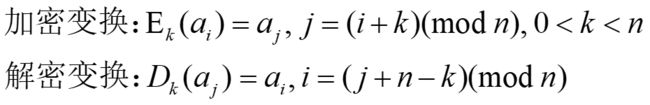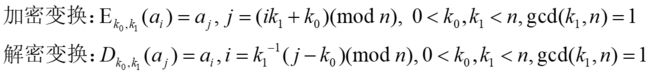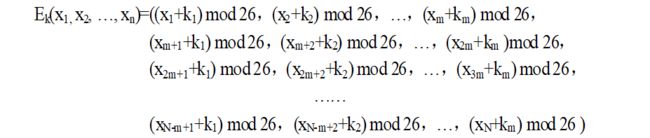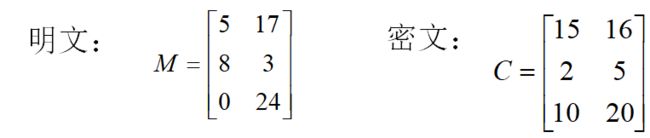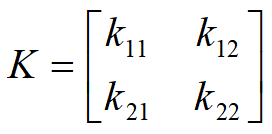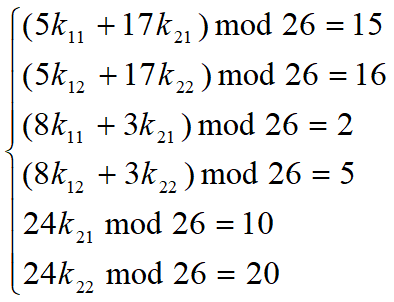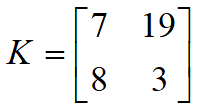替换（代换）密码技术【密码学笔记】

教材《应用密码学》-- 西安电子科技大学出版社

概念

将明文中的每一个字符均被替换成另一个字符（密文字符），接收者对密文做反向替换就可以恢复出明文。

替换密码是基于符号替换的密码技术，以符号的置换来达到掩盖文明信息的目的。

1、单字符单表替换密码技术

单表单字符的含义是对明文中所有的字符都使用一个固定的映射，即：

• 任何明文加密、密文解密均使用同一个密码表。
• 明文中相同的字母，必被加密成相同的密文字母。

（1）乘法密码技术

 

乘法密码技术的密匙是k。k满足gcd(k,n)=1，若n为素数，则有n-2个密匙（k=1是恒等变换，即加密后的密文和明文是一样的，应当舍弃）；若n不是素数，则有φ(n)-1个密匙（同样是舍弃了为1的情况）。

解密变换中的 k^-1 为 k 对模 n 的逆（也叫做 k 关于 n 的逆元），写作k^-1(mod n) 或 k^-1，满足：

　　

要求 k, n 互质，否则 k 关于n的逆元不存在。

【例1】

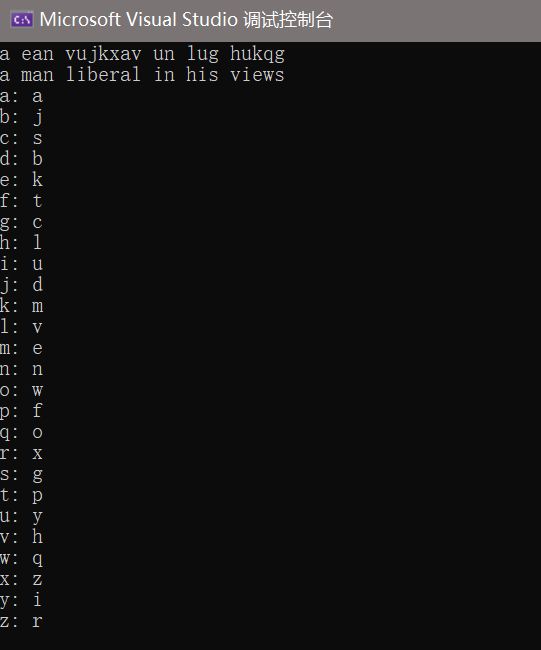
英文字母 n = 26，取密匙 k = 9。

明文：m = a man liberal in his views

密文：c = a ean vujkxav un lug hukqg

根据 k=9, n=26 ， 9^-1(mod 26) = 3

测试代码：

#include 
#include <string>
#include 
#include 
#include 
#include 
using namespace std;

char encypt(char c) {
    if (c != ' ')
        return (c - 'a') * 9 % 26 + 'a';//未考虑大小写
    return ' ';
}

char decode(char c) {
    if (c != ' ') {
        return (3 * (c - 'a')) % 26 + 'a';//未考虑大小写
    }
    return ' ';
}

void drawMapTable() {
    //未考虑大小写
    for (char cc = 'a'; cc <= 'z'; cc++){
        cout << cc << ": " << encypt(cc) << endl;
    }
}

int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL

    string s;
    
    getline(cin, s);
    for (int i = 0; i < s.length(); i++) {
        cout << encypt(s[i]);
    }
    cout << endl;
    getline(cin, s);
    for (int i = 0; i < s.length(); i++) {
        cout << decode(s[i]);
    }
    cout << endl;
    drawMapTable();
    return 0;
}

View Code

（2）加法（移位）密码技术

加法密码技术是一种移位替换密码技术。

密匙的个数为n-1个，k = n 时为恒等变换，进行舍弃。

 【例2】

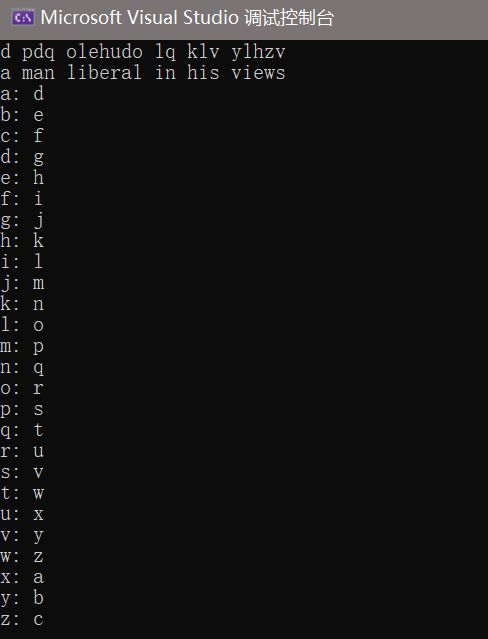
 凯撒密码，对26个英文字母进行移位替换，取n = 26，k = 3.

#include 
#include <string>
#include 
#include 
#include 
#include 
using namespace std;

char encypt(char c) {
    if (c != ' ') {
        return ((c - 'a') + 3) % 26 + 'a';
    }
        
    return ' ';
}

char decode(char c) {
    if (c != ' ') {
        return ((c - 'a' - 3 + 26)) % 26 + 'a';
    }
    return ' ';
}

void drawMapTable() {
    //未考虑大小写
    for (char cc = 'a'; cc <= 'z'; cc++){
        cout << cc << ": " << encypt(cc) << endl;
    }
}

int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL

    string s;
    
    getline(cin, s);
    for (int i = 0; i < s.length(); i++) {
        cout << encypt(s[i]);
    }
    cout << endl;
    getline(cin, s);
    for (int i = 0; i < s.length(); i++) {
        cout << decode(s[i]);
    }
    cout << endl;
    drawMapTable();
    return 0;
}

View Code

（3）仿射密码技术

乘法密码技术和加法密码技术的结合体

 k₀,k₁为该加密算法的密匙，当k₀=0时，仿射密码技术退化为乘法密码技术，当k₁=1时，退化为加法（移位）密码技术。

【例3】

记Z₂₆ = {0,1,2……25}表示26个字母，选取k₁满足gcd(k1,26)=1，则k1可取 [φ₍₂₆₎ - 1] = 11个数之一，k₀可取(0,26]区间的26个数（取n时不再会出现恒等变换了），则密匙空间的大小为（k₁,k₀）= 11*26 = 286 。

若选定(k₁,k₀)=(7,3)， 7^-1(mod 26)=15

 测试代码：

#include 
#include <string>
#include 
#include 
#include 
#include 
using namespace std;

char encypt(char c) {
    if (c != ' ') {
        return ((c - 'a') * 7 + 3) % 26 + 'a';
    }
        
    return ' ';
}

char decode(char c) {
    if (c != ' ') {
        //书上没写，实际操作时，这里还是要加上一个n，否则出现负数会计算错误
        return ((c - 'a' - 3 + 26) * 15) % 26 + 'a';
    }
    return ' ';
}

void drawMapTable() {
    //未考虑大小写
    for (char cc = 'a'; cc <= 'z'; cc++){
        cout << cc << ": " << encypt(cc) << endl;
    }
}

int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL

    string s;
    
    getline(cin, s);
    for (int i = 0; i < s.length(); i++) {
        cout << encypt(s[i]);
    }
    cout << endl;
    getline(cin, s);

    for (int i = 0; i < s.length(); i++) {
        cout << decode(s[i]);
    }
    cout << endl;
    drawMapTable();
    return 0;
}

View Code

2、单字符多表替换密码技术

 

1、Vigenere（费杰尔或维吉尼亚）密码技术

（1）加密

 

（2）解密

　　密钥的第一个字符被加到明文的第1个、第m+1个、第2m+1个、第3m+1个字符上（进行mod26运算），密钥的第二个字符被加到明文的第2个、第m+2个、第2m+2个、第3m+2个字符上，依此类推。
　　解密函数D_k和加密函数一样，只是运算时使用的是减法而不是加法，假设密文Y=(y₁，y₂，…，y_n)，则解密函数为：

（3）密匙

对于Vigener密码， 密匙是一个字符序列，比如，选择的密匙为vector，用数值表示则K=(21,4,2,19,14,17)，用来加密明文：here is how it works

加密方法过程如下：对第一个明文字符循环后移21位的字符替换，对第二个明文字符循环后移4位的字符替换，如此循环下去。

【例4】

 英文字母表n = 26，选择密匙 K = somuch，明文  m = a man liberal in his veiws 

 测试代码：

#include 
#include <string>
#include 
#include 
#include 
#include 
using namespace std;

//string k = "vector";
string k = "somuch";
 

int main() {
#ifdef LOCAL
    fstream cin("data.in");
#endif // LOCAL

    string s;

    getline(cin, s);
    //encrypt
    int index = 0;
    for (int i = 0; i < s.length(); i++) {
        if (s[i] != ' ') {
            cout << (char)((s[i] - 'a' + k[index % k.length()] - 'a') % 26 + 'a');
            index++;
        }
        else        
            cout << ' ';
    }
    cout << endl;
    //getline(cin, s);

    //for (int i = 0; i < s.length(); i++) {
    //    cout << decode(s[i]);
    //}
    //cout << endl;
 
    return 0;
}

View Code

 书上给的结果是 ：s amh nptsdun pf vun xpwke ，错了一个字符，可在线验证

2、Vernam（弗纳姆）密码技术

加密方法：将明文和密匙分别表示成二进制序列，再对他们进行模二加法，就是异或。

根据异或的特性（与自己异或结果为0），可以知道：

加密：c = m_i xor k_i

解密：m = c_i xor k_i

为了增强Vernam密码技术的安全性，要避免密匙的重复使用。假设我们可以做到密匙是真正的随机序列，密匙的长度大于或等于明文的长度（避免出现循环使用的情况），一个密匙只使用一次，那么Vernam密码技术是经得起考研的。

 3、Hill（希尔）密码技术

 

【例】

设英文字母a,b,c,…,z分别编码为0,1,2,3,4,…,25。已知Hill密码中的明文分组长度n为2，密钥K是Z₂₆上的一个二阶可逆方阵，假设明文friday所对应的密文为pqcfku，试求密钥K。

明文 friday 对应的编码为：5，17，8，3，0，24
密文 pqcfku 对应的编码为：15，16，2，5，10，20

由于 n = 2（分组长度），所以可得

　　
可以设K为：

　　

 于是有：

可得：

 

 所以密匙K为：

---

  　Hill密码技术可以较好地抗击统计分析攻击，但在面对已知明文的攻击时就很容易被破译，特别是在已知密钥矩阵行数的情况下。因此，Hill密码技术并不安全。

其基本加密思想是将n个明文字母通过线性变换将它们转换为n个密文字母的加密算法。解密时只需做一次逆变换即可。密钥就是变换矩阵。