非正则语言
NFA、\(\varepsilon-NFA\) 面向人构造系统
DFA面向机器构造系统
自动机理论非常完美!!
自动机的表述有纯数学形式的五元组形式(用来科学定义以及证明)、状态转移图(用来直观理解,也是一种数学工具)、状态转移表(编程用,用来定义数据结构比较好,面向计算机存储)
乔姆斯基把语言进行分类,0型、1型、2型、3型
每一种语言都有对应的处理装置:比如正则语言——有穷自动机 (正则表达式也行,以代数角度)、上下文无关语言——下推自动机 、 0型语言——图灵机
现阶段我们还是研究正则语言为主
接下来以研究正则语言(3型)的性质为主。
首先要讲额就是正则语言是有局限性的!!(而这个局限性就让我们在以后有发现上下文无关语言(2型)、上下文有关(1型语言)、0型语言的兴趣) 也就是其描述能力有限!!但是也要知道即使是更强的上下文无关文法,其描述能力也是受限的。
注意:这里我们衡量语言的描述能力,比较抽象,不好说。所以我们以语言对应处理装置的自动机处理能力为标准衡量语言描述能力!!!
也就是0型语言对应的图灵机处理能力是最强的!
正则语言性质:
- 有限性
- 封闭性
- 判定性
有限性:
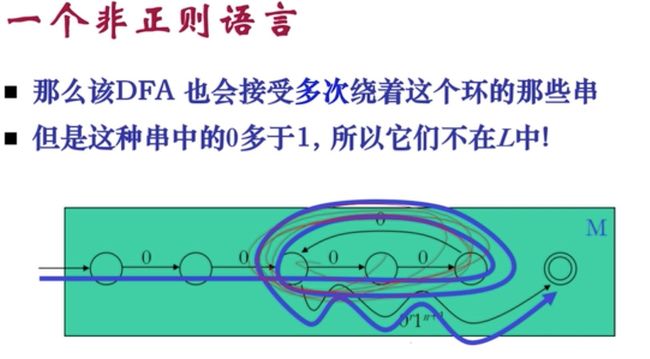
现在我们来看看,什么语言不能被正则语言对应的有限自动机处理
上面的B、C找不到正则表达式,也就找不到有限自动机(如果是正则语言,必然有它的处理装置——正则表达式或者DFA)
D能找到DFA。。
也就是有些语言不是正则语言!!!
DFA中的F指的是有限状态。而正则语言可能是有限的、也可能是无限的。我们的有限自动机理论厉害之处就是用有限的状态竟然可以描述多达无穷的语言。可怕!! Nb!
有穷的描述来处理无穷的东西,太屌了!!
抽屉原理呗!
也就是串不能过长,串太长就不能满足正则语言了(参考泵定理)
封闭性
如果有一个正则语言,那么在这个正则语言经过特定规定运算(并、连接、Kleene闭包)后仍然是正则的
在交、逆、同态、逆同态下也是封闭的
以数学方面的正则表达式方向证明:
有时候,用补语言的正则表达式我们可以分析出,但是类别太多,巨麻烦。换思路:自动机。我们可以试着写出补语言的DFA,嘻嘻
上面对自动机求补,只能是DFA,不能对NFA求补
要是求NFA的补,先把NFA变成DFA,再对DFA求补
还要一点要记住,正则表达式不能直接转化为DFA,他要通过NFA过渡,准确的说是\(\varepsilon\) -NFA。
逆也封闭,证明略
除此之外,还有幂次方、同态、逆同态也都是封闭的。证明略
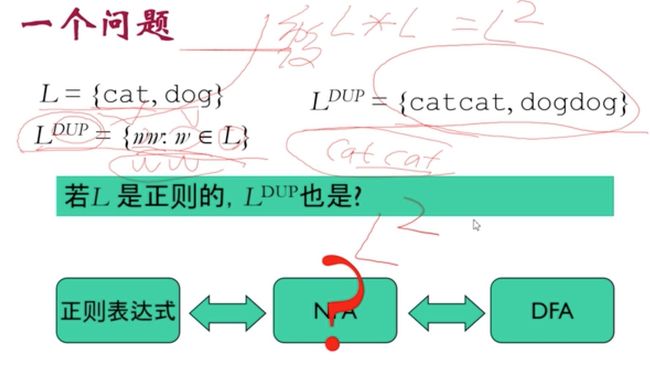
duplicate运算不封闭
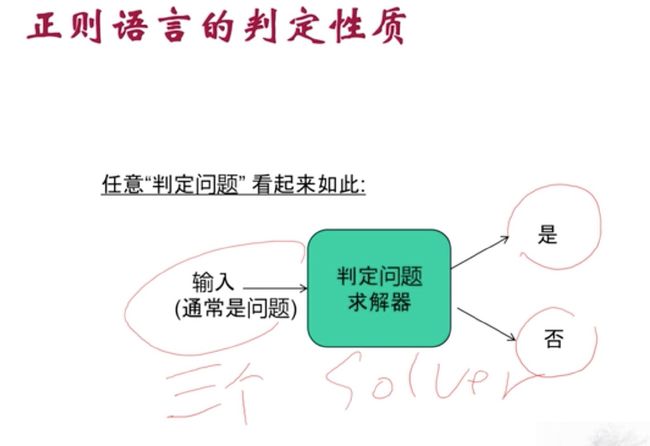
判定性
上面三个问题输进来,判断是否
- w是否属于L
- L是否是空
- L有穷或者无穷
可以判定语言是否是有穷还是无穷(因为有限自动机的有限指的是状态数有限,语言集合有可能有穷,也有可能无穷)
给出正则语言,根据正则语言可以写出自动机,然后对自动机做如下删减,可以判定该自动机(或者说该正则语言)是有穷还是无穷。。