第五章 形状匹配的特征提取(2)霍夫变换,线变换、圆变换、椭圆检测等及简化
第五章 形状匹配的特征提取(2)霍夫变换,线变换、圆变换、椭圆变换、参数空间分解
5.5 霍夫变换
5.5.1 概述
a. 霍夫变换是一种在图像中定位基础形状元素的技术,例如提取直线、矩形、椭圆等;霍夫变换的优势是对基本元素的查找可以达到接近模板匹配的结果,但是速度更快(采用了更简洁的描述方式);
这是一种基于evidenct-gathering(类似投票制)的方法,基于对模板匹配过程的重定义;HF定义了一种从图像点到累加器(霍夫空间)空间的映射,这一映射基于对目标形状的描述函数,以降低匹配过程和描述的资源消耗;
5.5.2 直线描述
a. 直线描述,截距式y=mx+c,齐次式Ay+Bx+1=0,其中A=-1/c,B=m/c;则直线可以描述为参数对(A,B),也就是在笛卡尔系里由两个点(x1,y1)(x2y2)确定的直线,在对偶的AB空间中,(x1,y1)(x2,y2)表现为直线形式,经过其中某点的直线族表现为AB空间内直线上的点,因此直线AB表现为(x1,y1)(x2,t2)对应直线的交点,根据特征点在AB空间形成的直线,对各个交点进行投票得到累加器空间(需要注意这里存在取整近似)峰值图,对峰值进行迭代提取即可得到有效的直线坐标,AB空间点,并计算出笛卡尔空间的直线方程;
b. 图像中所有共线的元素将定义共同交点(A,B),霍夫变换基于对每个点(xi,yi)追踪所有的双线进行计数,追踪到的每个有效点增加数组的一个元素,则直线提取问题转化为在累加器空间中定位最大值的问题;
考虑在笛卡尔系中直线具有连续性特征,通常在对偶的参数空间对直线进行描述;霍夫变换一般得到的是直线数据,需要结合图像信息确定线段的长度;
c. HF的直线检测过程实际上是提取出点密度更高的直线区域,基本的问题是定义一个合适的累加器空间,在应用时,Bresenham的画线算法可以用于生成累加器空间的投票机制,通过从累加器空间到边缘数据的计算可以确定显著峰值对应的边缘点集;;
d. 此外还可以使用基于极坐标描述的参数化方式,使用过原点的直线对应的垂线段描述,得到极坐标霍夫直线检测,ρ=x cos(θ)+y sins(θ),则对应到笛卡尔描述有
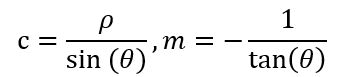
其θ-ρ二维累加器数组对应地调整为正弦波形式s,并根据正弦曲线交点进行投票;
这种基于极坐标的映射方法优势在于对直线的描述更固定,且对参数θ和ρ的范围进行了有效的限定,因此更加稳定和实用;
基于该方法,将直线上的点描述为正弦波,在θ-ρ参数空间中依据正弦曲线交点对直线参数进行投票;
e. 补充
(参考https://blog.csdn.net/m0_37264397/article/details/72729423)
霍夫变换基本过程,


5.5.3 圆的霍夫变换
a. 对应的曲线方程可以按照显示或参数形式给出,圆的显示定义有
(x-x_0 )2+(y-y_0 )2=r2
该方程的对偶形式为,笛卡尔空间X-Y中由至少3个(x,y)坐标确定的圆和参数空间X0-Y0中,以(x,y)为圆心,不确定的r的三维空间的若干圆(实际上是对某一个r,产生一组圆)的交点;每个边缘点定义了一个动态半径的累加器空间投票椎体,并生成累加器空间峰值图;
b. 基于极坐标的描述有,x=x0+rcos(θ),y=y0+rsin(θ),则
x0=x-rcos(θ),y0=y-rsin(θ)
该方法的优势在于允许解决参数问题,需要注意θ并不是一个自由参数,但是它定义了曲线的轨迹,曲线(或者表面)表面的轨迹通常称为点扩散函数;
c. 代码实现,假设半径是定值,作为输入参数,则累加器在实现上表现为二维形式,离散θ(控制投票的粒度granularity,一般越精细则参数空间越精确)生成投票圆;
圆的绘制采用Bresenham画圆算法而不是极坐标实现以得到完整圆的轨迹,且避免离散操作的定义,Bresenham算法可以用来生成一个八分圆上的点,其余点通过反射得到;
考虑到直接采用三维方式需要过大的计算量,因此通常的软件实现方式采用霍夫梯度法实现,通过估计边缘点梯度方向近似计算可能的圆心,然后对半径进行计算,步骤如下,
I、估计圆心
1、把原图做一次Canny边缘检测,得到边缘检测的二值图
2、对原始图像执行一次Sobel算子,计算出所有像素的邻域梯度值(得出边缘点-圆心指向矢量,也就是认为边缘点的梯度方向一般是径向的)
3、初始化圆心空间N(a,b),令所有的N(a,b)=0
4、遍历Canny边缘二值图中的所有非零像素点,沿着梯度方向画线,将线段经过的所有累加器中的点(a,b)的N(a,b)+=1
5、统计排序N(a,b),得到可能的圆心
II、估计半径(针对某一个圆心a,b)
1、计算Canny图中所有非0点距离圆心的距离
2、距离从小到大排序,根据阈值,选取合适的可能半径(比如3和3.5都被划为半径值3中)
3、初始化半径空间r,N®=0
4、遍历Canny图中的非0点,对于点所满足的半径r,N®+=1
5、统计得到可能的半径值
d. 易见,在该类提取中也可以引入其他信息作为条件,调整对应边缘点投票的权重;
5.5.4 霍夫变换椭圆检测
a.对圆可以通过相似性变换进行椭圆映射,有
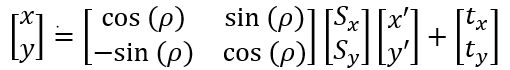
其中(x’,y’)表示圆坐标,ρ表示朝向。(Sx,Sy)是尺度因子,(tx,ty)是平移量,也就是包括了旋转、缩放、平移;即有
![]()
![]()
其中,
![]()
该等式对应于椭圆的极坐标表示;其中θ仍然表示量化参数不需要考虑,椭圆形状被特化为参数表:(a0,b0, ax,bx,ay,by ),其中包含一个冗余参数(考虑约束条件ax bx+ay by=0),则椭圆通过中心坐标(a0,b0)和三个形状参数(实际椭圆的形状描述证实通过5个参数,包括中心坐标、长短轴、旋转角度)(ax,bx,ay,by ),其中形状参数应该被重新进行组织以描述椭圆的大小和朝向,即有
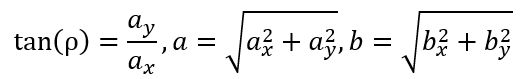
则椭圆中心位置可以通过
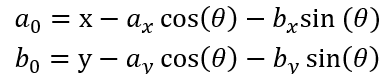
进行计算;
初步看来该方法的直接实现仍然是基于不同层次的变量参数分步估计,例如梯度法计算中心坐标,生成x,y,生成角度,然后利用累加器统计投票;不然就要构造一个5维空间,导致大额的空间和时间开销;
实现可以参考:https://blog.csdn.net/traumland/article/details/51089786
5.5.5 参数空间分解
5.5.5.1 直线的参数空间缩减
a. 对于直线,可以通过从图像信息中计算斜率将累加器空间降至一维,即
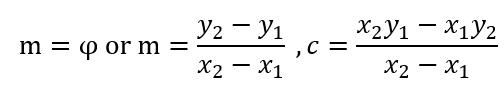
对应的极坐标形式可以表示为
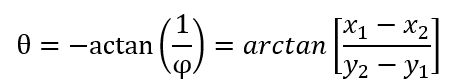
在实现时只需要针对其中一个参数构造累加器就可以得出目标直线,在实现上分别对两个参数使用一维霍夫变换,共同确定目标直线的角度和位置;也就是相当于认为边缘点自身具有方向信息,该方向信息理论上可以反映边缘的朝向;
5.5.5.2 圆的参数空间缩减
a. 通常可以考虑圆的不同几何属性以分解参数空间,一种常用的几何关系是二阶方向导数几何属性所给定的,
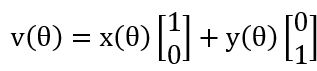
其中x(θ)=x0+rcos(θ),y(θ)=y0+rsin(θ),该函数实际上以x0,y0为中心定义了一个θ矢量集,其终点形成圆;进一步有
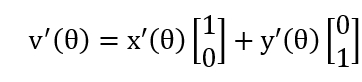
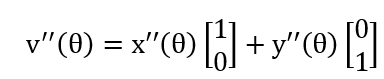
其中x’(θ)=-rsin(θ),x’’ (θ)=-rcos(θ),y’(θ)=rcos(θ),y’’ (θ)=-rsin(θ),其中一阶导数定义了切矢量,二阶导数类似于矢量函数;
则一阶导数角度的正切Φ’(θ)=y’(θ)/x’(θ) =-1/tan(θ) ;
则

即有(x0,y0)(x(θ),y(θ))直线y(θ)=Φ’’ (θ)(x(θ)-x0 )+y0,该等式独立于半径参数,因此可以独立用于二维累加器确定位置坐标(x0,y0),其对偶形式映射表现为
![]()
也就是根据已知的边缘点(x(θ),y(θ)),在对偶空间生成一条投票线,Φ^’’ (θ)和(x(θ),y(θ)已知,构造x0-y0投票线,确定圆心后进一步使用一维累加器确定半径;
b. 参数分解的关键问题是ϕ’‘的确定,常用方法为依据边缘方向信息或者依据点对信息;
(1)边缘方向信息(单一梯度法),Φ‘’ (θ)=1/(Φ‘(θ) ) ,则

Φ‘(θ)可以通过在边缘点的梯度方向得到;
(2)点对信息,对一组边缘点对(x1,y1 )(x2,y2 ),在圆上存在(x(θ),y(θ)),使
Φ’ (θ)=(y2-y1)/(x2-x1),θ=((θ1+θ2))/2
则有 Φ’’ (θ)=(x2-x1)/(y2-y1),实际上点对点连线的对应的中垂线是有效投票线,则该点坐标为
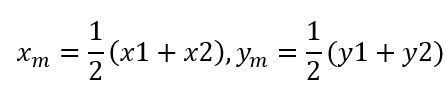
则投票直线表示为
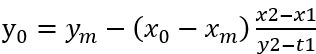
一般在1010或1212像素的淋浴范围内寻找点对,且不采用距离过近的点对以避免误差,距离太远则可能导致来自不同圆;峰值的宽度取决于点对间隔,一般峰值越窄,噪声水平越高;
5.5.5.3 椭圆的参数空间缩减
a. 尽管椭圆具有更复杂的几何形状,但仍然具有二阶方向导数所定义的角度的几何关系,

则一二阶方向导数正切角:
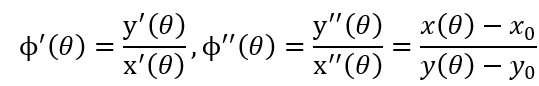
但和圆不同的情况是,在一般情况下,角度Φ’ (θ)和Φ’’ (θ)不具有正交关系,综合梯度几何关系和点对几何关系,仍然可以对ϕ’’(θ)进行求解,点对(x1,y1)(x2,y2)的中点坐标设为(xm,ym ),该点与(x0,y0)决定的直线即ϕ’’ (θ),且
tan(θ)=tan(1/2(θ1+θ2)),
ϕ^’’ (θ)=ym/xm
对存在平移的椭圆调整为

其中(xT,yT )是点对切线的交点,则有
ϕ’’ (θ)=(AC+2BD)/(2A+BC),
其中A=y1-y2,B=x1-x2,C=ϕ1+ϕ2,D=ϕ1∙ϕ2;ϕ1ϕ2表示切线斜率;则
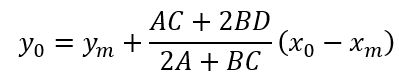
通过两组点对计算椭圆中心坐标,然后可以通过一个三维的参数空间或两个而为参数空间计算旋转或缩放数据;