【吴恩达机器学习笔记】005 梯度下降(Gradient Descent)
一、引入
在前几节课我们讲到,我们希望能够找到曲线拟合效果最好的线条,这样的线条的误差最小,所以就转化成了下面这幅图所表达的内容。
我们有一些函数,这些函数会有n个参数,我们希望能得到这个函数的最小值,为了方便计算,我们从最简单的入手,让参数的个数仅有两个。对于这个函数,我们会给定初始的参数θ0和θ1,不断改变他们的值,从而改变函数值,直到我们找到我们希望的函数的最小值。所以,我们引入梯度下降算法。
二、什么是梯度?
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z)T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
三、梯度上升与梯度下降
在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数f(θ)的最小值,这时我们需要用梯度下降法来迭代求解。但是实际上,我们可以反过来求解损失函数 -f(θ)的最大值,这时梯度上升法就派上用场了。
四、梯度下降算法理解
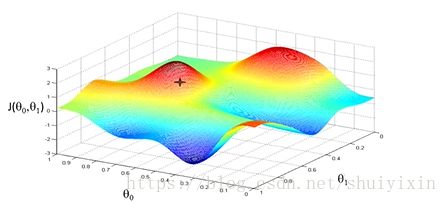
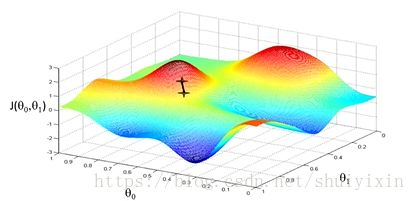
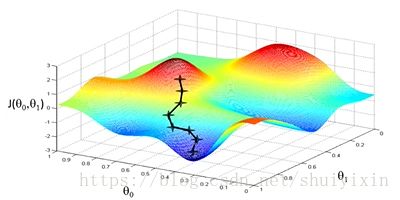
下面这幅图,可以看做两座高山,我们希望能以最快的速度下山,那我们每一步需要朝向什么方向呢?假设我们从图上“+”位置开始下山,我们假定第二幅图中的方向就是下山最快的方向,那达到第二个位置的时候,相当于处在一个新起点,我们会照着第一步的方法,再选择一个新的我们认为最好的方向走第二步,如下面第三幅图所示。我们照着这种方式,一步一步走下去,直到山脚。也就是在图中,不管从哪个位置开始,每走到一个位置,就需要判断,找到最好的位置走第二步。而这种找最好位置的方法就是梯度下降算法。即每到一个位置,求解当前位置的梯度,沿着梯度的负方向(图像上当前最陡峭的位置)向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了图像的局部最低点。(注:局部最低点不一定是整个数据集的最低点)。
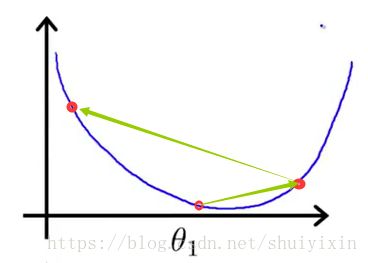
因为走到的是局部最低点,不是整体最低点,所以梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。而且,相近的起点,可能最终的结果也有很大差别。比如下图,虽然起点与上面情况起点相差很少,但是通过下降梯度算法,最终的位置却到了另外一个局部最低点。
五、梯度下降算法定义上面这个公式就是梯度下降的算法,那这个算法表达的是什么含义呢?
首先,给出所有的符号的定义,便于大家理解:
:= : 这个符号是赋值符号;
= : 这个符号是等于符号;
α : 这个符号是下降速率(learning rate),它控制我们用多大的幅度来更新θj。例如在下山的例子中,它控制下山的速率;
要注意的是,这里的等于和赋值与C++等编程语言是不同的,以C++为例,=表示赋值,==表示等于。
在横线的下面,写了一个Correct:Simultaneous update(正确的:同时更新),这个是什么意思呢?大家对比一下下面两组公式,一个是正确的,一个是不正确的。
我们能发现,区别在于,前面的θ0和θ1是同时更新的,然后在做迭代,而后面的是先求出θ0,然后求θ1,为什么必须要同时更新呢?
我自己的理解是: 迭代时, θ0和θ1是需要上一组的θ0和θ1,θ0和θ1是一组,即不可分的,同一组的θ0和θ1是由上一组的θ0和θ1生成的,相邻两组之间的θ0和θ1不能构成另一个θ0或θ1。
所以我们要记住一句话:梯度下降,必须要同步更新;不同步更新,不是梯度下降算法。
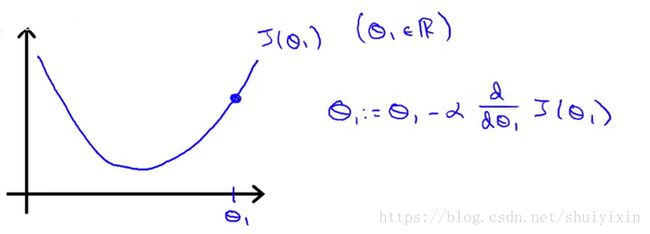
我们再简化一下,假设只有一个参数θ1,并且假设图像如下图所示。
那我们能从图像看出最低点的位置,计算机怎么更加精确地找到呢?假设θ1从最低点的右侧开始对图像进行初始化,函数的导数大于0,α是速率,大于0,这个时候,新的θ1小于上一个θ1。
同理,如果θ1从最低点的左侧开始对图像进行初始化,函数的导数小于0,α是速率,大于0,这个时候,新的θ1大于上一个θ1。 当然,如果恰好θ1就是最小值,那这个时候,导数等于0,θ1的值就不会变了。
那么,会不会出现一种情况,当初始化的值不为最小值时,进行梯度下降处理后到了最小值的另一边呢?答案是肯定的,因为α的值没有限制,所以在取值时要注意。如果α的值过小,下降速率会很慢,就像下面左边的图一样。当然,如果α的值太大,就会出现右图的情况,最后无法收敛,离最小值越来越远。
六、举例
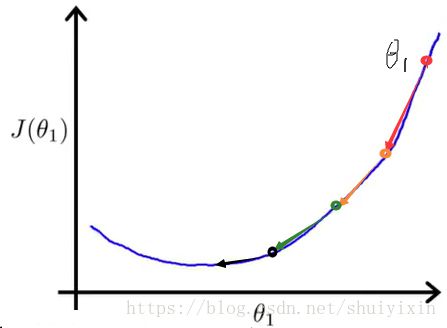
假设上图是我们经过试验计算得到的代价函数。我们从图上的θ1点(图中最右上角的点)开始做梯度下降。当α的值比较恰当(不会过大或过小),会得到下图,第一次做梯度下降时,函数图像比较陡,导数值比较大,下降的比较快,第二次做梯度下降时,图像较第一次更加平缓,导数值变小,下降速度变慢,继续做梯度下降,直到收敛到最低点,最终得到最优解。