机器学习笔记（九）聚类算法及实践（K-Means,DBSCAN,DPEAK,Spectral_Clustering）

这一周学校的事情比较多所以拖了几天，这回我们来讲一讲聚类算法哈。

首先，我们知道，主要的机器学习方法分为监督学习和无监督学习。监督学习主要是指我们已经给出了数据和分类，基于这些我们训练我们的分类器以期达到比较好的分类效果，比如我们前面讲的Logistic回归啊，决策树啊，SVM啊都是监督学习模型。无监督学习就是指我们就只有数据，没有分类结果，然后根据数据进行建模能够给出哪些样本是属于一类的一个过程，通常我们就称之为聚类。

今天我主要介绍以下几种最常见的聚类算法，包括K-Means算法，基于密度的聚类（DBSCAN）算法，密度最大值算法（DPEAK），谱聚类算法，基本上也是从易到难，从原理讲讲我自己的理解，希望对大家有用。

====================================================================

K-Means算法。

原理上来讲，K-Means算法其实是假设我们数据的分布是K个sigma相同的高斯分布的，每个分布里有N1，N2……Nk个样本，其均值分别是Mu1，Mu2……Muk，那么这样的话每个样本属于自己对应那个簇的似然概率就是

这个套路我们就很熟悉了，下面就是取对数似然概率，要求似然概率的最大值，给它加个负号就可以作为损失函数了，考虑到所有簇的sigma是相等的，所以我们就可到了K-Means的损失函数

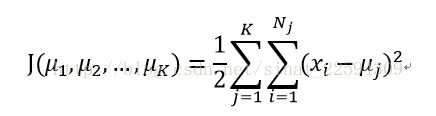
接着我们对损失函数求导数为0，就可以得到更新后最佳的簇中心了

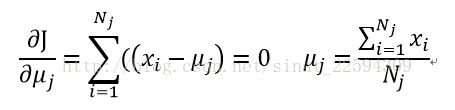
这样我们就得到了所谓的K-Means算法

1 初始选择K个类别中心。

2 将每个样本标记为距离类别中心最近的那个类别。

3 将每个类别中心更新为隶属该类别所有点的中心。

4 重复2,3两步若干次直至终止条件（迭代步数，簇中心变化率，MSE等等）

现在我们回过头来看看K-Means算法的问题。

首先，正如我刚开始介绍它的时候，它是假设数据服从sigma相同的混合高斯分布的，所以最后分类的结果肯定是若干个类圆形的区域，这就很大程度上限制了它的应用范围，如果我们的数据是那种比较奇葩的形状，比如什么扇形啊，圆环啊，你会发现K-Means的效果其实不是很叫人满意。

其次，你得给出这个分类的数目K啊，有一定的先验条件还好，如果是两眼一抹黑，怎么确定呢？猜呗，或者试呗，用一定的评价标准选择最佳那个就成。还有就是初始簇中心的选择，K-Means的结果对初值是敏感的，比如说样本分为三个簇，你一开始把两个中心定在某一个簇中，还有一个中心处在另外两个簇的中间，这样最后的结果很可能是那两个簇被划分成一类，还有一个簇被强行划分成两个簇这样。所以为了解决这个初值敏感问题，又提出了K-Means++算法，它的做法就是你先随机指定第一个簇中心，然后计算所有点到该簇中心的距离，以这个距离作为权值来选择下一个簇中心，一定程度上可以解决簇中心初值选择不合理的问题。

最后还有一个问题，就类似于上一篇我们讲的SVM一样，如果我们采用线性可分SVM方法，一个异常点就可以把我们的分割超平面带跑偏导致泛化能力被削弱。K-Means中我们采用均值来更新簇中心，同样的，一个异常点会导致新的这个簇中心发生比较大的偏离，而且再更新的时候我们还是要考虑那个异常点，所以就不会得到比较好的效果。

说了这么多K-Means的缺点都显得它一无是处了，我们还是要说K-Means作为一种最经典的聚类算法，它简单，快速，在应对大数据的时候相对优势会比较大，有的时候还可以作为其他聚类算法中的一步。

====================================================================

DBSCAN算法。

前面讲了K-Means算法主要针对那种类圆形区域数据的聚类，相对来说应用范围窄了一点。而密度聚类可以弥补这个缺点，可用于任何形状的聚类。这个算法需要我们调节两个参数，半径sigma，最小数目m，先介绍该算法的一些概念

核心对象：对于一个对象它的sigma领域内至少有m个对象，那我们就称之为核心对象

直接密度可达：如果一个对象处在一个核心对象的sigma领域内，那称这两个对象直接密度可达

密度可达（相连）：如果一个对象a和b直接密度可达，对象b和c也是直接密度可达，那么我们称a和c是密度可达的，也称这两个对象是密度相连的。

DBSCAN的算法就是我们先找到一个核心对象，从它出发，确定若干个直接密度可达的对象，再从这若干个对象出发，寻找它们直接密度可达的点，直至最后没有可添加的对象了，那么一个簇的更新就完成了。我们也可以说，簇其实就是所有密度可达的点的集合。

它的优势在哪儿呢？

首先，它对这个簇的形状没要求，只要这些点密度可达我们就把它归为一个簇，这样不管你的形状多奇葩，最后我们都能把它分到同一个簇当中。

其次，我们可以想一下那些异常点，它偏离正常对象很多，所以它既不是核心对象，然后对其它的点又不是密度可达的，所以最后就被剩了出来没被分类。因此DBSCAN算法还有一定的剔除异常值的功能，当然里，这里也要注意，如果我们的sigma值太大或者m太小，还是会导致一些异常值浑水摸鱼混进某些簇里或者自成一类等等，总而言之，还是要根据分类的结果进行调参，寻找最佳的分类方式。

====================================================================

DPEAK算法

密度最大值算法可以看成是基于以上两种算法的一种拓展吧，它的主要优势在于确定簇中心和排除异常值。

具体的做法怎么做呢，我们首先给定一个半径范围r，然后对我们所有的样本，计算它的r邻域内的样本数目记作它的局部密度记作rho，第二步，计算每个样本到密度比它高的点的距离的最小值记作sigma，有了这两个参数就可以进行我们下一步的筛选工作了，具体分成以下四种情况：

1 rho很小，sigma很大。这个样本周围的样本量很小，但是到比它密度大的点的距离还挺远的，这说明啥，它是个远离正常样本的异常值啊，在偏僻的小角落里搞自己的小动作啊，果断踢了它呀。

2 rho很大，sigma也很大。这个样本周围样本量很大，并且要找到比它密度还大的点要好远好远，这说明这个点是被众星环绕的啊，它就是这个簇的王，我们往往把它确定为簇中心。

3 rho很小，sigma也很小。样本周围的样本量很小，但要找到样本密度比它大的点没多远就有，说明这个点是一个处在边缘上的点，往往是一个簇的边界。

4 rho很大，sigma很小。该样本周围的样本量很大，但是密度比它还大的居然也不远，这种情况只会发生在你处在了簇中心的旁边时，很可惜，也许你是这个簇的核心成员，但你做不了这个簇的王。

好的，基于每个样本的rho和sigma，我们大概就能确定它们各自的所扮演的角色了，我们把大反派异常值从样本中剔除，然后把我们找到的rho和sigma都很大的点作为簇中心，再利用K-Means或者DBSCAN算法进行聚类就能得到相对比较好的结果。

====================================================================

谱聚类

这是要说的最后一种聚类算法了，我发现今天讲聚类公式确实不多，但是打字也好累啊！！！

谱聚类是一种基于图论的一种聚类方法，我希望通过一种比较直观的方式给大家解释清楚它到底在干什么。

首先引入几个概念，谱聚类肯定要讲什么是谱，还有就是相似度矩阵，度矩阵和拉普拉斯矩阵。

谱：方阵的特征值（不是方阵的话就是左乘其转置所得方阵的特征值）称之为谱，其中最大值称为谱半径。

相似度矩阵W：n个样本则建立一个n*n的矩阵，矩阵第i行第j列的值为第i个样本和第j个样本的某种相似度。

度矩阵D：一个n*n的对角阵，第i行第i列的值为相似度矩阵中第i行的所有值之和。

拉普拉斯矩阵L：度矩阵减去相似度矩阵即为拉普拉斯矩阵。

好了，基于以上这些概念，我们来考虑这样一种情况。对于这样m个样本，它们是属于同一类的，那么它们是不是可以建立一个m*m的相似度矩阵W，该矩阵还是个对称阵，紧接着可以求得它的度矩阵和拉普拉斯矩阵，巧就巧在这个矩阵是个半正定的，证明如下

所以拉普拉斯矩阵的特征值大于等于0。从度矩阵的定义我们知道，它的对角元素等于相似度矩阵每一行的和，因此拉普拉斯矩阵乘以一个全1的向量得到全为0的一个列向量，因此拉普拉斯矩阵存在一个0的特征值，对应特征向量为全1向量，也就是说

同样的假如有另外一个类的n个样本，同样的，对于它而言，有

假设这两个类的样本毫无相似度，那么它们两个样本混合在一起的相似度矩阵可以表示为

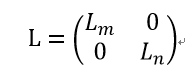
我们已经知道Lm和Ln对应于特征值0的特征向量了，那么可以求得L对于m的两个特征向量

那么我们可以明显的看到，对应于L最小特征值0的两个特征向量可以明显的把两个种类分开，所以推广开来我们就知道，通过拉普拉斯矩阵最小的K个特征值对应的特征向量进行聚类，我们就能确定对应的样本所属的类别。当然现实情况中不可能像我们推导的这么美丽，全1全0的情况很少出现，因为样本之间多多少少有些藕断丝连的关系，但据此对特征向量进行聚类就已经能确定样本所属的种类，这就是我们所说的谱聚类。

最后重复一下谱聚类的算法过程

1 计算相似度矩阵，度矩阵及拉普拉斯矩阵。

2 计算拉普拉斯矩阵前K小的特征值对应的特征向量。

3 将这K个特征向量组成一个新的矩阵，对其行向量进行聚类。

4 行向量的聚类结果代表了原始样本的聚类结果。

====================================================================

好了，这大概就是我今天想讲的算法的所有内容了，下面就是喜闻乐见的调包环节了，前面被用烂的鸢尾花数据今天终于派不上用场了，所以第一步我们先造一点数据看看

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
#造数据
N=500
centers=4
data,y=ds.make_blobs(N,centers=centers,random_state=0)
#原始数据分布
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
cm = matplotlib.colors.ListedColormap(list('rgbm'))
plt.scatter(data[:,0],data[:,1],c=y,cmap=cm)
plt.title(u'原始数据分布')
plt.grid()
plt.show()

结果如下

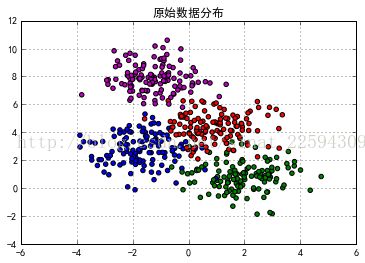
OK，我们先用K-Means试试

#K-Means
from sklearn.cluster import KMeans
model=KMeans(n_clusters=4,init='k-means++')
y_pre=model.fit_predict(data)
plt.scatter(data[:,0],data[:,1],c=y_pre,cmap=cm)
plt.title(u'K-Means聚类')
plt.grid()
plt.show()

结果是

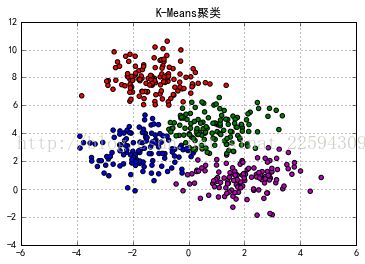
分类结果相当之好啊，除了局部靠的比较近的几个点小有错误，整体还是叫人满意的。但不知道少年你是否还记得我之前说的，K-Means有个先验条件，它是假设数据满足方差相同的高斯分布的，所以我们故意使这些数据的方差不同来看看聚类效果是否会大受影响

#方差不等数据
data2,y2=ds.make_blobs(N,centers=centers,cluster_std=(2,2,5,8),random_state=0)
plt.scatter(data2[:,0],data2[:,1],c=y2,cmap=cm)
plt.title(u'原始数据分布')
plt.grid()
plt.show()
model2=KMeans(n_clusters=4,init='k-means++')
y_pre2=model2.fit_predict(data2)
plt.scatter(data2[:,0],data2[:,1],c=y_pre2,cmap=cm)
plt.title(u'K-Means聚类')
plt.grid()
plt.show()

结果如下

果然，聚类后的数据是一坨一坨那种，并不能把原始数据中间那两类分开，所以这也验证了我们之前讲的K-Means还是有其局限性的。

好啦，今天打了好多字呀……祝大家周末愉快，have a nice day~