【算法思维训练-剑指Offer联名 二】递归与循环篇
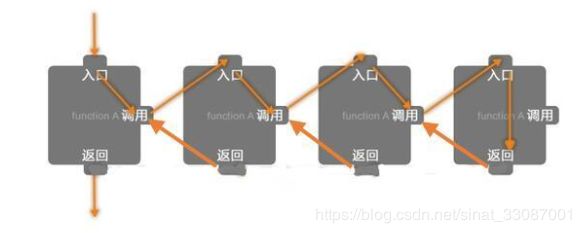
本篇是联名训练的第二篇,主题为递归与循环,如果我们需要重复地多次计算相同的问题,通常可以选择用递归或者循环两种不同的方法。递归是在一个函数的内部调用这个函数自身。而循环则是通过设置计算的初始值及终止条件,在一个范围内重复运算。
递归与循环
循环很常见,就是for、while、do while这样子,我们平时使用的也较为频繁,我们重点关注下递归的优缺点:
- 优点:代码简洁。基于递归实现的代码比基于循环实现的代码要简洁很多,更加容易实现。
- 缺点一:效率较低。递归由于是函数调用自身,而函数调用是有时间和空间的消耗的:每一次函数调用,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,而且往栈里压入数据和弹出数据都需要时间。这就不难理解上述的例子中递归实现的效率不如循环**【时间】。另外,递归中有可能很多计算都是重复的,从而对性能带来很大的负面影响。递归的本质是把一个问题分解成两个或者多个小问题。如果多个小问题存在相互重叠的部分,那么就存在重复的计算【空间】**。
- 缺点二:调用栈溢出。递归还有可能引起更严重的问题:调用栈溢出。前面分析中提到需要为每一次函数调用在内存栈中分配空间,而每个进程的栈的容量是有限的。当递归调用的层级太多时,就会超出栈的容量,从而导致调用栈溢出。
所以在对性能和时间要求不严格,以及限制递归次数的前提下,使用递归比较好,比较代码简洁清爽。反之,如果有强要求的时候,可以考虑使用循环。从递归的优缺点也可以归纳出递归的三大要素:
- 第一要素:明确你这个函数想要干什么。先不管函数里面的代码什么,而是要先明白,你这个函数的功能是什么,要完成什么样的一件事。
- 第二要素:寻找递归结束条件。我们需要找出当参数为啥时,递归结束,之后直接把结果返回,请注意,这个时候我们必须能根据这个参数的值,能够直接知道函数的结果是什么。
- 第三要素:找出函数的等价关系式。我们要不断缩小参数的范围,缩小之后,我们可以通过一些辅助的变量或者操作,使原函数的结果不变。
算法训练
《剑指offer》关于递归与循环的算法训练共有4题:斐波那契数列【难度3】、跳台阶【难度3】、变态跳台阶【难度2】,矩形覆盖【难度3】。
斐波那契数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。n<=39
分析
按照第一篇学习过程中的方法来分析,分为如下几个要点:
- 数列为斐波那契数列,其特点是,某一项的值等于其前两项的和
- 边界条件:n<=39
解法
当然了,最直观的解法当然是直接用递归公式去做:
public class Solution {
public int Fibonacci(int n) {
//设置边界条件
if(n>39||n<0)
return -1;
if(n==0)
return 0;
if(n==1)
return 1;
if(n>1&&n<=39)
return Fibonacci(n-1)+Fibonacci(n-2);
return -1;
}
}
但是提交结果是:

那么该怎么优化呢?不难看出,其实这里做了很多重复的计算,例如f(5)实际上是f(3)+f(4)…一直到f(1)+f(0)。如果能寄存中间值,就不用浪费这些性能了。**如果你使用递归的时候不进行优化,是有非常非常非常多的子问题被重复计算的。因此,使用递归的时候,必要须要考虑有没有重复计算,如果重复计算了,一定要把计算过的状态保存起来。
public class Solution {
public int Fibonacci(int n) {
if(n>39||n<0)
return -1;
if(n==0)
return 0;
if(n==1)
return 1;
int result=0;
int first=0;
int second=1;
for(int i=2;i<=n;i++){
result = first+second;
first=second;
second=result;
}
return result;
}
}
跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
分析
按照第一篇学习过程中的方法来分析,分为如下几个要点:
- 实际Demo举例:如果只有 1 级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。
- 边界条件:共有n个台阶,n为1到n之间的正整数
我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。因此n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里,我们不难看出这实际上就是斐波那契数列了。
解法
public class Solution {
public int JumpFloor(int target) {
if(target<1) return -1;
if(target==1) return 1;
else if(target==2) return 2;
else return JumpFloor(target-1)+JumpFloor(target-2);
}
}
以及低性能损耗的循环版本。
public class Solution {
public int JumpFloor(int target) {
if(target<1) return -1;
if(target==1) return 1;
else if(target==2) return 2;
else{
int result=0;
int first=1;
int second=2;
for(int i=3;i<=target;i++){
result = first+second;
first=second;
second=result;
}
return result;
}
}
}
变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
分析
确实有够变态的,不过按照第一篇学习过程中的方法来分析,分为如下几个要点:
- 实际Demo举例:如果只有 1 级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。如果有3级台阶,那就有f(1)+f(2)+一次跳3级共有4种,如果有4级台阶,那就是
- 边界条件:共有n个台阶,n为1到n之间的正整数
我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2),最后一种选择是第一次跳3级,此时跳法数目等于后面剩下的n-3。因此n级台阶的不同跳法的总数归纳为f(n)=f(n-1)+f(n-2)+f(n-3)…+f(n-n)=f(0)+f(1)+…f(n-1)=f(n-1)+f(n-1)=2*f(n-1)
解法
这个时候
public class Solution {
public int JumpFloorII(int target) {
if(target<1) return -1;
if(target==1) return 1;
else {
return 2*JumpFloorII(target-1);
}
}
}
以及低性能损耗的循环版本。
public class Solution {
public int JumpFloorII(int target) {
if(target<1) return -1;
if(target==1) return 1;
else {
int result=0;
int last=1;
for(int i=2;i<=target;i++){
result=2*last;
last=result;
}
return result;
}
}
}
矩形覆盖
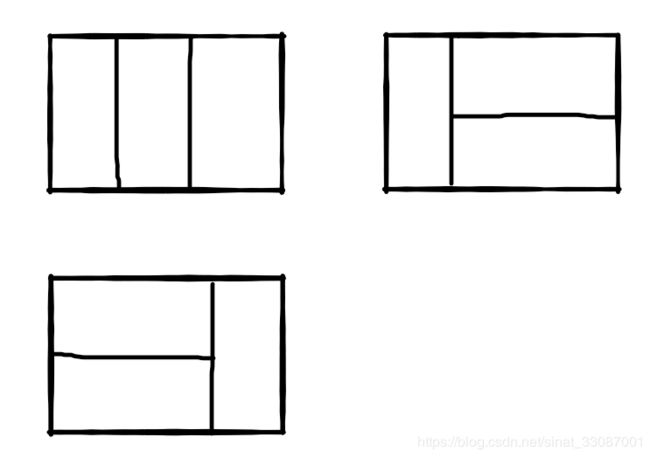
我们可以用2X1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2X1的小矩形无重叠地覆盖一个2Xn的大矩形,总共有多少种方法?比如n=3时,2*3的矩形块有3种覆盖方法:
分析
同样按照之前的方式去分析,不过按照第一篇学习过程中的方法来分析,分为如下几个要点:
- 实际Demo举例:如果只有 1 个矩形,那显然只有1种方法。如果有2个矩形,那就有2种方法了:一种是两个都竖着,另外一种就是两个都横着。如果有3 个矩形,那就有f(1)+f(2)共3种方法。
- 边界条件:共有n个矩形,n为1到n之间的正整数
- 摆放方式:只有两种,竖着放或者横着放。
用第一个1×2小矩形去覆盖大矩形的最左边时有两个选择,竖着放或者横着放。当竖着放的时候,右边还剩下2×2的区域,这种情形下的覆盖方法记为f(2)。接下来考虑横着放的情况。当1×2的小矩形横着放在左上角的时候,左下角必须也横着放一个1×2的小矩形,而在右边还还剩下2×1的区域,这种情形下的覆盖方法记为f(1)
解法
public class Solution {
public int RectCover(int target) {
if(target<1) return 0;
if(target==1) return 1;
else if(target==2) return 2;
else {
return RectCover(target-1)+RectCover(target-2);
}
}
}
以及低性能损耗的循环版本。
public class Solution {
public int RectCover(int target) {
if(target<1) return 0;
if(target==1) return 1;
else if(target==2) return 2;
else {
int result=0;
int first=1;
int second=2;
for(int i=3;i<=target;i++){
result=first+second;
first=second;
second=result;
}
return result;
}
}
}
思考
说实话递归虽然牛逼但还是蛮烧脑的,主要考虑想象能力。估计递归在二叉树上用的比较多吧,不过递归这里也有一些收获:
- 增强如上一篇所说的理论:构建一个简单的Demo,因为有些问题是显而易见的递归,但有些问题不一定看得出来是递归,这个时候就需要去归纳,归纳出规律自然而然就能写出代码
- 代码简洁和性能损耗在递归这里不可兼得啊,一定要依照需求出发,看看目的是什么,场景是什么,什么时候该用递归,什么时候该用循环
- 递归感觉有点儿分治的感觉,结果回归条件。
多练练抽象思维,还是有好处。