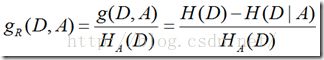决策树类算法理论

熵：

如果一件事有k种可的结果，每种结果的概率为 pi（i＝1…k ）

该事情的信息量：

熵越大，随机变量的不确定性越大。

信息增益：

特征A对训练数据集D的信息增益g(D,A)， 定义为集合D的经验熵H(D)与特征A给定条件下的经验条件熵H(D|A)之差

换句话说，就是原信息集下的信息量－在A特征条件下的信息集的信息量

信息增益越大，信息增多，不确定性减小

信息增益率：

信息增益率定义:特征A对训练数据集D的信息增益比定义为其信息增益与训练数据D关于特征A的值的熵HA(D)之比

注：p：每个唯独上，每个变量的个数／总变量个数

ID3算法：

ID3算法的核心是在决策树各个子节点上应用信息增益准则选择特征，递归的构建决策树，具体方法是:从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归调用以上方法，构建决策树。

解释：在做每次选择差分枝的时候，以不确定性最小点作为loss fuction，直到无法细分

缺点：

1.ID3算法只有树的生成，所以该算法生成的树容易产生过拟合，分得太细，考虑条件太多。

2. 不能处理连续属性

3. 选择具有较多分枝的属性，而分枝多的属性不一定是最优的选择。

4.局部最优化，整体熵值最小，贪心算法算子节点的分支

C4.5算法：

基于ID3算法， 用信息增益比来选择属性， 对非离散数据也能处理， 能够对不完整数据进行处理。

采用增益率（GainRate）来选择分裂属性。计算方式如下：

CART算法：

CART算法选择分裂属性的方式是比较有意思的，首先计算不纯度，然后利用不纯度计算Gini指标。

计算每个子集最小的Gini指标作为分裂指标。

不纯度的计算方式为：

pi表示按某个变量划分中，目标变量不同类别的概率。

某个自变量的Gini指标的计算方式如下：

计算出每个 每个子集的Gini指标， 选取其中最小的Gini指标作为树的分支（Gini（D）越小，则数据集D的纯度越高）。连续型变量的离散方式与信息增益中的离散方式相同。

随机森林：

随机生成n颗树，树之间不存在关联，取结果的时候，以众数衡量分类结果；除了分类，变量分析，无监督学习，离群点分析也可以。

生成过程：

1.n个样本，随机选择n个样本（有放回），训练一颗树
从原始训练数据集中,应用bootstrap方法有放回地随机抽取 K个新的自助样本集,并由此构建 K棵分类回归树,每次未被抽到的样本组成了 K个袋外数据(Out-of-bag,OOB)
2.每个样本有M个属性，随机选m个，采取校验函数（比如信息增益、熵啊之类的），选择最佳分类点

3.注意，每个树不存在枝剪
4.将生成的多棵树组成随机森林,用随机森林对新的数据进行分类,分类结果按树分类器的投票多少而定

树的个数随机选取，一般500，看三个误差函数是否收敛；变量的个数一般取均方作为mtry

GBDT：

DT步骤：

GBDT里面的树是回归树！

GBDT做每个节点上的分支的时候，都会以最小均方误差作为衡量（真实值－预测值）的平方和／N，换句话说，就是存在真实线l1，预测线l2，两条线之间的间距越小越好。

BT步骤：

GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差 ，这个 残差就是一个加预测值后能得真实值的累加量 。

换句话说，就是第一次预测的差值记为下一次预测的初始值，一直到某一次计算出的差值为0，把前n次的结果相加，就是一个真实预测。

Lg与Dt类的差异（抄的图）：

lg是连续的0，1曲线，而dt是0，1的分段函数，Dt类可以自主选择变量承担高维，非线性，可以同时处理离散和连续变量。

分布式R RF介绍：

local R RF简单小栗子：

library('randomForest')
setwd("~/Desktop")
train_origin<-read.table('trian.txt',header = T,fill = T)
test_origin<-read.table('test.txt',header = T,fill = T)
train_test1<-train_origin
train_test1<-train_test1[,-9]
train_test1$tag<-as.factor(train_test1$tag)
train_test1$risk_level<-as.factor(train_test1$risk_level)

##模型训练
model2<-randomForest(tag~zhi_score+phone_score+guide_score+risk_level+high_orders+airport_orders+company+consume+area,data=train_test1,importance=T,proximity=T,mtry=3,ntree=500)

##预测

model2_prdeiction_test<-predict(model2,train_test1)

##正误矩阵

table(model2_prdeiction_test,train_test1$tag)

##各变量的重要性MeanDecreaseAccuracy：随机变量赋值，MeanDecreaseGini：变量异质性
importance(model2)

##寻找最优的ntree
plot(model2$err.rate[,1],type='l') ##总误差分布
plot(model2$err.rate[,2],type='l') ##误判正误差分布
plot(model2$err.rate[,3],type='l') ##正判误误差分布

##寻找最有的深度mtry
rate<-rep(0,5)
for( i in 1:(ncol(train_test1)/2))
{
  set.seed(112)
  model<-randomForest(tag~zhi_score+phone_score+guide_score+risk_level+high_orders+airport_orders+company+consume+area,data=train_test1,importance=T,proximity=T,mtry=i,ntree=500)
  rate[i]= mean(model$err.rate)#计算基于OOB数据的模型误判率均值 
}

##测试集

test_test1<-test_origin
test_test1<-test_test1[,-9]
test_test1$tag<-as.factor(test_test1$tag)
test_test1$risk_level<-as.factor(test_test1$risk_level)


model2_prdeictio2_test<-predict(model2,test_test1)
table(model2_prdeictio2_test,test_test1$tag)

如果有任何算法、代码疑问都欢迎通过公众号发消息给我哦，已经给你们准备好资料大礼包了。