图像识别(一)
准备重新做一些图像方面的东西,在去年的时候尝试过mnist手写图片的分类那个小项目,这次打算深入学习下图像方面的东西并且写出一些优秀的代码传到github上。
首先我们下载了关于keras的一些资料,并且找到了一篇tensorflow学习笔记,那么正好复习一下关于tensorflow的有关知识。
Tensorflow:
使用图graph来表示计算,在会话Session中执行图,使用张量Tensor来代表数据,通过变量Variable来维护状态,使用供给feed和取回Fetches来输入输出数据。
先写一个简单的代码:
import tensorflow as tf
matrix1 = tf.constant([[2.0,2.0]])
matrix2 = tf.constant([[3.0,1.0]])
product = tf.multiply(matrix1,matrix2)
with tf.Session() as sess:
result = sess.run(product)
print(result)
此时得出正常的结果[[6,2]],如果我们使用matmul进行矩阵乘法,那么将会报错,因为维度不正确,我们更改matrix1和matrix2的维度使得他们能够进行矩阵乘法。
matrix1 = tf.constant([[2.0,2.0]])
matrix2 = tf.constant([[3.0],[1.0]])
product = tf.matmul(matrix1,matrix2)
得出正确的结果[[8]]
常用运算命令:加add 减subtract 乘multiply 除divide 矩阵相乘matmul 不需要参数的时候也可以直接使用符号。
tensorflow使用tensor数据结构来代表所有的数据,操作间传递的数据都是tensor。之后我们测试一下变量相关的代码:
state = tf.Variable(0,name = 'counter')
one = tf.constant(1)
new_value = tf.add(state, one)
update = tf.assign(state,new_value)
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
print(sess.run(state))
for _ in range(3):
sess.run(update)
print(sess.run(state))
通过new_value进行加一的操作,通过update进行赋值,以此对变量进行更新。其中init_op中的global_variables_initializer()使得全部的变量初始化.
def demo_feed():
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)
output = input1 * input2
with tf.Session() as sess:
result = sess.run([output],feed_dict = {input1:7.0,input2:2.0})
print(result)
if __name__ == "__main__":
demo_feed()
程序通过设置占位符placeholder来将变量处于一个待命的状态,在后面run中使用了feed_dict通过传入字典的方式来喂给占位符数据。值得一提的是[output]会使得结果从一个数字变成一个一维数组。
MNIST数据集测试
MNIST数据集是图像问题比较经典的一个问题,目标是识别手写的数字图片。
每一张图片在处理过程中是一个28*28的向量,因此mnist数据集中的图片就是784维向量空间中的点,因此mnist.train.images是一个[60000,784]的张量,第一个维度用来索引图片,第二个维度用来索引像素点。张量里的元素都表示图片里像素值的强度,介于01之间。mnist.train.labels是一个[60000,10]的张量,代表0-9个值。
softmax回归模型
softmax回归模型用来给不同的对象分配概率,并且使得总概率加和为1。x回归模型后的概率是e为底的x次幂除以全部项的e为底的x次幂。
x = tf.placeholder(tf.float32, [None, 784], name="X_input")
W = tf.Variable(tf.zeros([784, 10]), name='W')
b = tf.Variable(tf.zeros([10]), name='b')
我们通过一个占位符来定义输入:它是一个不知道多少数量的784维的向量集。而权重w则是784个维度是10的向量集,代表着这784个像素点每一个点对10个数字的权重各是多少。偏置b则是对10个数字结果进行偏置。
y = tf.nn.softmax(tf.matmul(x, W) + b)
通过x和w矩阵相乘加上偏置后通过softmax以得到最后的结果。我们的训练是不断修正w和b使得模型更加具有分类性能。
train = tf.train.GradientDescentOptimizer(0.01).minimize(entropy)
for i in range(1000):
batch_x, batch_y = mnist.train.next_batch(100)
feed = {x: batch_x, yactual: batch_y}
sess.run(train, feed_dict=feed)
使用梯度下降步长设置为0.01,迭代1000次每个batch选择100个样本进行训练。这里我们应该注意以后要把要传入的数据feed单独写一行,集成在feed_dict后面会显得杂乱。
pred = tf.equal(tf.argmax(y, 1), tf.argmax(yactual, 1))
accuracy = tf.reduce_mean(tf.cast(pred, tf.float32))
print(sess.run(accuracy,feed_dict={x:mnist.test.images,yactual:mnist.test.labels}))
tf.equal(a,b)返回的是a,b逐个元素判断的true false列表
tf.argmax(a,1)返回的是a中每一行比较最大值的索引值,上文中返回真实结果yactual和返回预测结果y
tf.cast()把pred的true false转换成数字,预测对的就是1错的是0,然后求平均值,默认为1轴
最后我们得出0.9187的准确率
提到上面的entropy我们要了解一下交叉熵:
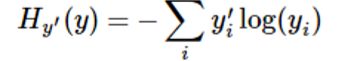
交叉熵用来衡量:在给定真实分布下,使用非真实分布的策略消除系统不确定性的大小。不确定性越小交叉熵越小,也被成为对数损失函数。前面的y`是实际的分布01,后面的y是预测的分布概率数值。
下一次尝试使用卷积神经网络处理这个数据集,识别率应该能有很大的提升。