CYK算法简介与实现

摘要

CYK算法是一个基于“动态规划”算法设计思想，用于测试串w对于一个上下文无关文法L的成员性的一个算法。CYK算法可以在 O(n3) O ( n 3 ) 的时间内得出结果。CYK算法是由三个独立发现同样思想本质的人（J. Cocke、 D. Younger和T. Kasami）来命名的。这篇博客将主要介绍乔姆斯基范式、CYK算法的流程以及其代码实现。

1. 乔姆斯基范式

任何一个非空且不含ϵ的上下文无关文法（CFL）都具有特殊形式的文法G。G中所有的产生式都属于以下两个简单的形式之一：
(1). A→BC A → B C ，其中A，B和C都是变元
(2). A→a A → a ，其中a是终结符
更进一步， G G 没有无用的符号。这样的文法就称为乔姆斯基范式或CNF。

将一个一般的CFL构造一个CNF的过程如下：
(1). 为每个出现在长度大于等于2的产生式中的终结符a创建一个新的变元A，该变元只有一个产生式 A→a A → a 。接着，可以用A来替代所有产生式中出现的a。现在，所有产生式或者是单个终结符，或者是至少两个以上的变元并且没有终结符。
(2). 把所有形式为 A→B1B2B3...Bk(k≥3) A → B 1 B 2 B 3 . . . B k ( k ≥ 3 ) 的产生式打断为以下一组产生式： A→B1C1,C1→B2C2,...,Ck−3→Bk−2Ck−2,Ck−2→Bk−1Bk A → B 1 C 1 , C 1 → B 2 C 2 , . . . , C k − 3 → B k − 2 C k − 2 , C k − 2 → B k − 1 B k 。
现在，所有的产生式都符合CNF的定义。

2. CYK算法介绍

CYK算法从一个CFL L的CNF文法 G=(V,T,P,S) G = ( V , T , P , S ) ，输入是T中的串 w=a1a2...an w = a 1 a 2 . . . a n 。该算法在 O(n3) O ( n 3 ) 的时间内构造出一个表明w是否属于L的表。表的结构如图。水平轴对应串 w=a1a2...an w = a 1 a 2 . . . a n 中的位置，图中假定 n=5 n = 5 。 xij x i j 是满足 A⇒˙aiai+1...aj A ⇒ ˙ a i a i + 1 . . . a j 的变元A的集合。特别地，如果S属于集合 x1n x 1 n ，那么w就属于L。

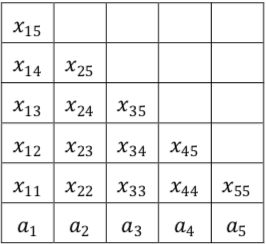
为了填写这个表，我们一行一行，自下而上地处理。每一行对应一种长度的子串。最下面一行对应长度为1的子串，倒数第二行对应长度为2的子串，以此类推。最上面一行就对应长度为n的子串，即w本身。计算该表的任何一个表项的方法如下：
(1). 对于最下面一行的表项，即 xii x i i ，是使得 A→ai A → a i 是G的产生式的变元A的集合。
(2). 对于不在最下一行的表项，我们需要找到符合以下条件的变元A的集合：
I. 整数k满足 i≤k<j i ≤ k < j
II. B属于 Xik X i k
III. C属于 Xk+1,j X k + 1 , j
IV. A→BC A → B C 是G的产生式

例如，对于下列CNF文法G的产生式:
S→AB|BC S → A B | B C
A→BA|a A → B A | a
B→CC|b B → C C | b
C→AB|a C → A B | a
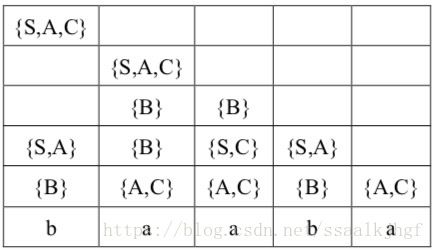
对L(G)测试 baaba b a a b a 的成员性所构造的表如下图所示。下以 x24 x 24 为例来展示 xij x i j 的计算。我们可以选择 k=2 k = 2 或 k=3 k = 3 。因此，必须考虑所有 x22x34∪x23x44 x 22 x 34 ∪ x 23 x 44 构成的产生体。这个串的集合是 {A,C}{S,C}∪{B}{B}={AS,AC,CS,CC,BB} { A , C } { S , C } ∪ { B } { B } = { A S , A C , C S , C C , B B } 。该集合中只有 CC C C 是 B→CC B → C C 的产生体，因此 x24={B} x 24 = { B } 。

3. CYK算法的实现

以下是CYK算法的核心函数。整个程序还包含了实现乔姆斯基范式的类、从文件读取乔姆斯基范式等关键功能的实现，由于篇幅原因不方便在此博客中全部展示。若要获取完整的可编译源文件，请访问Github：https://github.com/ssaalkjhgf/CYKAlgorithm.git

//************************************************************************************
//Use CYK algorithm to judge whether the string str is in the Chomsky normal form CFG
bool CYK(string str, const CNF& cnf) {
    //Get each word in the string str
    vector<string> sentence = split(str, ' ');
    int wordCount = sentence.size();

    //Allocate memory for CYKMat, a matrix of set storing all the parsing conditions of str[i..j]
    set** CYKMat = new set*[wordCount + 1];
    for (int i = 0; i <= wordCount; i++) {
        CYKMat[i] = new set[wordCount + 1];
    }

    //Preprocess the words, get the CYKMat[i][i]
    for (int i = 1; i <= wordCount; i++) {
        CYKMat[i][i] = cnf.produce(sentence[i - 1]);
    }
    //Calculate the rest part of CYKMat
    //For each length
    for (int length = 2; length <= wordCount; length++) {
        //For each starting position
        for (int i = 1; i <= wordCount - length + 1; i++) {
            //For each middle point of str[i..i+length-1]
            for (int k = i; k < i + length - 1; k++) {
                //Get the set of variables that CYKMat[i][k] and CYKMat[k+1][i+length-1] can produce
                set tmp = cnf.produce(CYKMat[i][k], CYKMat[k + 1][i + length - 1]);
                //Union
                CYKMat[i][i + length - 1].insert(tmp.begin(), tmp.end());
            }
        }
    }

    //If CYKMat[1][wordCount] consists of the starting symbol, accept the string
    if (CYKMat[1][wordCount].find(cnf.getStartSymbol()) == CYKMat[1][wordCount].end())
        return false;
    else
        return true;
}