将递归函数转换为非递归形式

1. 递归的调用原理：分而治之

为求一个大规模问题的问题，可以：
（1）将原问题划分成若干子问题
（2）子问题规模小到一定程序，可以直接求解，即存在递归终止的条件，称做递归出口。
（3）原问题分解的子问题总会向递归出口靠拢
（5）子问题求解后，可以将子问题求得的解合并得到原问题的解。

2. 使用机械方法将递归转换为非递归的准则

机械方法是指将任何递归函数转换为非递归函数有一套固定的规则，使用该规则可以将任何递归函数转换为非递归函数。
基本原理：
（1）当遇到递归函数调用但还没有到达它的递归出口条件时，需要将该函数的所有现场信息包括函数形参、局部变量保存到堆栈里。
如果递归函数有返回值，需要把返回值以参数的形式传出，该参数也要存放到堆栈里。比如：

int exmp(int n)
{   
     if(n<2)
         return n+1;
     else
         return exmp(n/2) * exmp(n/4);
}

需要转换为：

void exmp(int n,int& f)
{
    int u1,u2;
    if(n<2)
        f = n+1;
    else
    {
        exmp(n/2,u1);
        exmp(n/4,u2);
        f = u1*u2;
    }
}

压栈时需要把形参n f和局部变量u1 u2都存放到堆栈里。
（2）一次函数调用对应堆栈里的一个数据元素。如果形参和局部变量有多个数据，可以把它们放到结构体里。
（3）当函数调用返回时，需要对该函数对应的堆栈数据弹栈，以恢复调用者的现场信息；如果有数据需要传回，需要把返回值放到调用者对应的堆栈数据里。这样就可以利用子问题的解求出原问题的解。
（4）当前函数信息一定存放到堆栈的top中，它的调用者信息存放在它的上一个数据里。堆栈数据从栈顶到栈底的排列顺序就是函数间调用关系的相反顺序。

3. 使用机械方法将递归转换为非递归的步骤：

（1）设置一工作栈记录现场信息。
在递归函数中出现的所有参数、局部变量都必须用栈中相应的数据成员代替，除此之外还要存储返回语句标号域rd（如果递归函数会调用t个子函数，那么rd取值0~t+1）。这些信息可以用一个结构体存储：

typedef struct elem { // 栈数据元素类型
int rd;               //  返回语句的标号
Datatypeofp1 p1;      // 函数参数
 …
Datatypeofpm pm;
Datatypeofq1 q1;      // 局部变量
… 
Datatypeofqn qn; 
} ELEM;

（2）设置t+2个语句标号，分别是label 0 ~ label t+1
label 0: 递归函数第一条可执行语句，一般是处理满足递归出口条件时的语句
label t+1 ：设在函数体结束处，当每个递归函数返回时会调用这里。作用是：处理函数返回前需要做哪些工作。
label i(1<=i<=t)： 第i个递归子函数执行结束返回时需要执行的操作，通常是弹出当前函数的堆栈信息，并把计算结果回传给调用者
（3）增加非递归入口
处理第一个递归函数调用，把函数参数保存到堆栈中。其中rd=t+1。语句为：S.push(t+1,p1,...pm,q1,...qn)
（4）替换第i (i=1,…,t)个递归规则
假设函数体中第i (i=1, …, t)个递归调用语句为：recf(a1, a2, …,am)；则用以下语句替换：

S.push(i, a1, …, am)； // 实参进栈
goto label 0；
label i： x = S.top()；S.pop();
          ...

这里label i处理第i个递归函数返回时需要执行的操作。可以调用x = S.top();S.pop();弹出当前函数的堆栈信息。如果有数据需要传给调用者，可以继续调用S.top()获得调用者的数据并对它赋值。
（5）递归出口增加语句 goto label t+1
（6）添加标号为t+1的语句
label t+1的语句是固定的：根据递归返回地址rd跳转到相应的label。如果case t+1，表示处理完了最顶层的函数调用，函数结束。

switch ((x=S.top ()).rd) {
case 0 :  goto label 0;
break;
case 1 : goto label 1;
break;
……….
case t+1 : item = S.top(); S.pop(); // 返回
break;
default : break;
}

（7）改写嵌套和循环中的递归
对于嵌套递归调用。例如recf (… recf())改为：

exmp1= recf ( );
exmp2= recf (exmp1);
…
exmpk= recf (exmpk-1)

然后应用规则 4 解决
对于循环中的递归，改写成等价的goto型循环
（8）优化处理
由于（1）~（6）写的函数使用了goto语句，根据流程图找出相应的循环结构，从而消去goto语句

4. 优化前exmp函数的机械非递归实现：

typedef struct elem  //存储递归函数的现场信息
{
    int rd;          //返回语句的标号，rd=0~t+1
    int pn,pf;       //函数形参,pn表示参数n,pf表示参数f
    int q1,q2;       //局部变量,q1表示u1,q2表示u2
}ELEM;
class nonrec
{
    private:
        std::stack S;
    public:
        nonrec(void){}
        void replace1(int n,int& f);
        void replace2(int n,int& f);
};
void nonrec::replace1(int n,int& f)
{
    ELEM x,tmp;
    x.rd=3;                       //因为exmp内共调用2次递归子函数，t=2，所以td=t+1=3,压到栈底作监视哨
    x.pn=n;
    S.push(x);                    //调用最开始函数,递归的总入口。相当于调用exmp(7,f)
label0:
    if( (x = S.top()).pn < 2)     //处理递归出口,所有递归出口处需要增加语句goto label t+1。这也是递归语句第一条可执行语句
    { 
        S.pop();             
        x.pf = x.pn + 1;         //获得函数的解pf
        S.push(x);
        goto label3;             //因为递归出口语句执行完后需要处理函数返回,而lable t+1是用来处理函数返回需要做的工作的，所以需要goto lable3
       }

       x.rd = 1;                 //调用第一个递归函数,位于label0的后面，所以如果不满足递归出口会不断调用这里，直到满足递归出口
       x.pn = (int)(x.pn/2);
       S.push(x);                //一次调用使用一个堆栈数据
       goto label0;              //调用后开始进入函数内部，由于函数的第一条执行语句位于lable0，所以需要goto label0


label1: tmp = S.top();           //label1处理第1个递归函数返回时需要进行的处理，通常是pop自己的数据，然后把计算结果放到调用者对应的数据内
        S.pop();                 
        x = S.top();
        S.pop();
        x.q1 = tmp.pf;           //获取第1个递归函数计算的结果，并回传给上层函数的q1
        S.push(x);

        x.rd = 2;                //调用第二个递归函数
        x.pn = (int)(x.pn/4); 
        S.push(x);
        goto label0;

label2: tmp = S.top();           //从第二个递归函数中返回
        S.pop();
        x = S.top();
        S.pop();
        x.q2 = tmp.pf;
        x.pf = x.q1 * x.q2;
        S.push(x);
label3:                          //递归出口（label0)结束后会调用这里
        switch((x=S.top()).rd)
        {
            case 1:
            goto label1;
            break;
            case 2:
            goto label2;
            break;
            case 3:             //t+1处的label：表示整个函数结束
            tmp = S.top();
            S.pop();
            f = tmp.pf;        //最终的计算结果
            break;
            default:
            break;
        }
}

5. 去掉goto后优化的非递归实现步骤

将4的goto语句去掉，可以得出优化后的非递归实现步骤。不过下面的描述步骤用到了树的一些术语，比如根节点、叶子节点、节点。这是因为我们可以把递归函数看成一个个树节点，把函数间的调用关系看成树节点的边，把满足递归出口条件的函数看做叶子节点，把入口函数看成根节点。
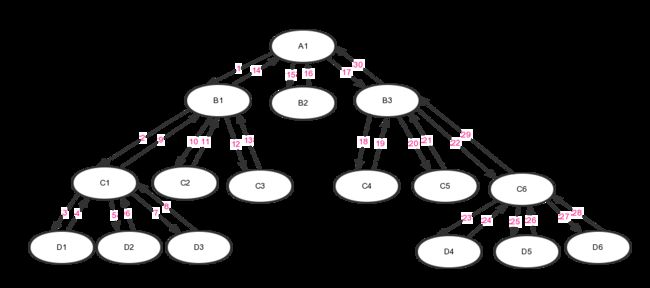
下面就是一个用树描述一个递归函数的调用关系图，该递归函数内部会调用3个子函数。其中1~30代表函数向下调用和向上回溯的顺序。它其实就是也是树节点后序遍历的顺序。

优化后非递归实现步骤为：
（1）增加非递归入口，压栈第一个节点。这个节点即是根节点。
（2）不断对递归函数“向下调用”，直到找到满足递归出口条件的叶子节点，比如A1->B1->C1->D1
（3）对满足递归出口的函数进行处理
（4）某函数处理完后，需要回溯到父节点，根据父节点找到新的处理函数。这需要根据它是不是调用者的最后一个调用函数分两种情况考虑。如果它不是最后一个调用函数（比如C1调用了D1 D2 D3三个子函数，D1处理完后还需要再处理D2，它不是调用者的最后一个调用函数）按照步骤（5）进行处理；如果是（比如D3是C1的最后一个调用函数）,说明它的父节点可以进行处理了。父节点处理完后，需要继续回溯到祖父节点，查看父节点是不是祖父节点的最后一个孩子，如果是，说明祖父节点也可以进行处理了。这个过程不断循环直到找到一个不是最后节点的祖先节点。
这个过程结束后产生两种结果：（1）得到的祖先是根节点。比如D6经过步骤28->29->30，到达根节点A1，函数结束；（2）获得一个不是最后一个节点的祖先节点且它不是根节点，比如D3->C1，C1不是B1的最后一个节点。获得这样的祖先节点后，按照（5）进行处理。
（5）如果函数不是调用者的最后一个调用函数，回溯到父节点，根据父节点找出它的下一个兄弟节点，把兄弟节点的信息压栈
（6）重新回到（1），直到步骤（4）回到根节点

只有在堆栈中新push了一个函数的信息后，才可以回到步骤（1）。
之所以要区分（5）与（6）两种情况，是因为：
（5）中新节点的回溯节点没变，新节点的回溯点依然是它的父节点，不需要向上回溯。而（6）中最后节点处理完后会导致父节点也要出栈即回溯节点变了，需要找到新的回溯节点并根据新的回溯节点找到新的处理节点。
从以上步骤中我们可知：堆栈中存储的树节点一定是从根到新压栈节点那条路径中的所有节点。

6. 优化后exmp的非递归实现：

void nonrec::replace2(int n,int& f)
{
    ELEM x,tmp;
    x.rd = 3;
    x.pn = n;
    S.push(x);
    do
    {
        while((x=S.top()).pn >= 2)       //不断对递归函数“向下调用”，直到满足出口条件。
        {
            x.rd = 1;
            x.pn = (int)(x.pn/2);
            S.push(x);
        }

        x = S.top();                    //满足出口条件，计算函数的解
        S.pop();
        x.pf = x.pn + 1;                //计算值保存在pf中，以便于让它的上层调用者使用。它的调用者数据存放子它对应堆栈数据的上一层
        S.push(x);

        while( (x = S.top()).rd == 2)   //满足出口条件后，需要回溯到父亲节点。需要分两种情况考虑，这里考虑它是父亲的最后一个节点，即rd==2的情况
        {
            tmp = S.top();
            S.pop();
            x = S.top();
            S.pop();
            x.q2 = tmp.pf;
            x.pf = x.q1 * x.q2;
            S.push(x);
        }

        if((x = S.top()).rd == 1)       //满足出口条件后，需要回溯到父亲节点。这里考虑该节点不是父亲节点的最后一个节点的情况
        {                         
            tmp = S.top();
            S.pop();
            x = S.top();
            S.pop();
            x.q1 = tmp.pf;
            S.push(x);
            tmp.rd = 2;
            tmp.pn = (int)(x.pn/4);
            S.push(tmp);
        }
    }while( (x = S.top()).rd !=3);
    x = S.top();
    S.pop();
    f = x.pf;    
}

7. 参考

北大张铭老师《数据结构与算法》公开课《递归转非递归》