一些计算机视觉该有的常识

K-means

已知样本集，其中每一个观测都是d-维实向量 ，K-means要把这m个样本划分到k个集合中(k ≤ m)，使得组内平方和(WCSS)最小。

标准算法

最常用的算法使用了迭代优化的技术。它被称为K-means而广为使用，有时也被称为Lloyd算法（尤其在计算机科学领域）。已知初始的k个聚类质心点，算法按照下面两个步骤交替进行。

• 分配(Assignment)：将每个样本i分配到聚类中，使得组内平方和（WCSS）达到最小。

•  更新(Update)：对于上一步得到的每一个聚类，以聚类中样本值的图心，作为新的均值点。

K-means面对的第一个问题是如何保证收敛，首先可以固定每个类的质心 ，调整每个样本的所属类别  来让WCSS减小；同样固定  ，调整每个类的质心  也可以让WCSS减小，这两个过程就是内循环中使J单调递减的过程。当WCSS递减到最小时，和c也同时收敛。（在理论上，可以有多组不同的和c值能够使得J取得最小值，但这种现象实际上很少见）。

iris

我们用非常著名的iris数据集。

from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
iris = datasets.load_iris()
X, y = iris.data, iris.target

data = X[:,[1,3]] # 为了便于可视化，只取两个维度
fig, plt.scatter(data[:,0],data[:,1])
plt.show()

欧式距离

def distance(p1,p2):
    tmp = np.sum((p1-p2)**2)
    return np.sqrt(tmp)

随机质心

def rand_center(data, k):
    """Generate k center within the range of data set."""
    n = data.shape[1]
    centroids = np.zeros((k,n)) # k个质心，每个质心的维度和样本维度相同
    for i in range(n):
        dmin, dmax = np.min(data[:, i]), np.max(data[:, i])
        centroids[:, i] = dmin + (dmax - dmin) * np.random.rand(k)
    return centroids

centroids = rand_center(data,2)
centroids

array([[ 2.15198267,  2.42476808],
       [ 2.77985426,  0.57839675]])

完整代码

kmeans有个缺点，就是可能陷入局部最小值，有改进的方法，比如二分k均值；也可以多计算几次，取效果好的结果。

def kmeans(data,k=2):
    def _distance(p1,p2):
        tmp = np.sum((p1-p2)**2)
        return np.sqrt(tmp)
    
    def _rand_center(data,k):
        """Generate k center within the range of data set."""
        n = data.shape[1] # features
        centroids = np.zeros((k,n))
        for i in range(n):
            dmin, dmax = np.min(data[:,i]), np.max(data[:,i])
            centroids[:,i] = dmin + (dmax - dmin) * np.random.rand(k)
        return centroids
    
    def _converged(centroids1, centroids2):
        # if centroids not changed, we say 'converged'
         set1 = set([tuple(c) for c in centroids1])
         set2 = set([tuple(c) for c in centroids2])
         return (set1 == set2)
    
    m = data.shape[0] # number of entries
    centroids = _rand_center(data,k)
    c = np.zeros(m, dtype=np.int) # track the nearest centroid
    assement = np.zeros(m) # for the assement of our model
    converged = False
    
    while not converged:
        old_centroids = np.copy(centroids)
        for i in range(m):
            # determine the nearest centroid and track it with label
            min_dist, min_index = np.inf, -1
            for j in range(k):
                dist = _distance(data[i],centroids[j])
                if dist < min_dist:
                    min_dist, min_index = dist, j
                    c[i] = j
            assement[i] = _distance(data[i], centroids[c[i]])**2
        
        # update centroid
        for j in range(k):
            centroids[j] = np.mean(data[c==j], axis=0)
        converged = _converged(old_centroids, centroids)
   
    return centroids, c, np.sum(assement)

由于算法可能局部收敛的问题，随机多运行几次，取最优值

best_assement = np.inf
best_centroids = None
best_c = None

for i in range(10):
    centroids, c, assement = kmeans(data,2)
    if assement < best_assement:
        best_assement = assement
        best_centroids = centroids
        best_c = c

data0 = data[best_c==0]
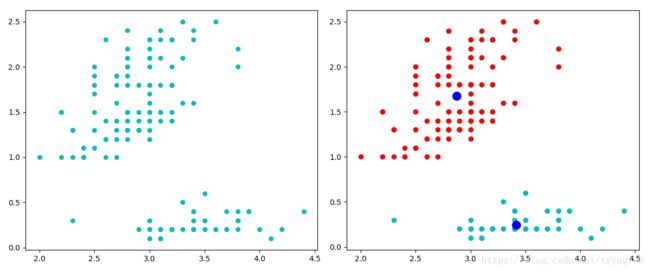
data1 = data[best_c==1]

如下图，我们把数据分为两簇：

fig, (ax1,ax2) = plt.subplots(1,2,figsize=(12,5))
ax1.scatter(data[:,0],data[:,1],c='c',s=30,marker='o')
ax2.scatter(data0[:,0],data0[:,1],c='r')
ax2.scatter(data1[:,0],data1[:,1],c='c')
ax2.scatter(centroids[:,0],centroids[:,1],c='b',s=120,marker='o')
plt.show()

最大似然估计

最大似然估计是一种确定模型参数值的方法。确定参数值的过程，是找到能最大化模型产生真实观察数据可能性的那一组参数。同时我们将找到的参数值称为最大似然估计（maximum likelihood estimates，MLE）。

最大似然估计总是能精确地得到解吗？

简单来说，不能。更有可能的是，在真实的场景中，对数似然函数的导数仍然是难以解析的（也就是说，很难甚至不可能人工对函数求微分）。因此，一般采用期望最大化（EM）算法等迭代方法为参数估计找到数值解，但总体思路还是一样的。

为什么叫「最大似然（最大可能性）」，而不是「最大概率」呢？

我们先来定义 P(data; μ, σ) 它的意思是「在模型参数μ、σ条件下，观察到数据 data 的概率」。值得注意的是，我们可以将其推广到任意数量的参数和任何分布。

另一方面，L(μ, σ; data) 的意思是「我们在观察到一组数据 data 之后，参数μ、σ取特定的值的似然度。」

上面的公式表示，给定参数后数据的概率等于给定数据后参数的似然度。但是，尽管这两个值是相等的，但是似然度和概率从根本上是提出了两个不同的问题——一个是关于数据的，另一个是关于参数值的。这就是为什么这种方法被称为最大似然法（极大可能性），而不是最大概率。

什么时候最小二乘参数估计和最大似然估计结果相同？

结果表明，当模型被假设为高斯分布时，MLE 的估计等价于最小二乘法。 

Kullback–Leibler divergence

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。

KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

定义

对于离散随机变量，其概率分布P和Q的KL散度可按下式定义为 

 对于连续随机变量，其概率分布P和Q可按积分方式定义为

流形（manifolds）

流形（英语：Manifolds），是局部具有欧几里得空间性质的空间，是欧几里得空间中的曲线、曲面等概念的推广。欧几里得空间就是最简单的流形的实例。地球表面这样的球面则是一个稍微复杂的例子。一般的流形可以通过把许多平直的片折弯并粘连而成。 

任何一个流形都可以嵌入到足够高维度的欧氏空间中 (Whitney嵌入定理)。

流形的特殊性质：

• 不满足平行公设：存在过空间中任意两点的平行直线(测地线)
• 球面：任意两条测地线(大圆弧)都相交
• 测地三角形的内角和不一定等于180度