重温数据结构：二叉树的常见方法及三种遍历方式 Java 实现

读完本文你将了解到：

树的分类有很多种，但基本都是 二叉树 的衍生，今天来学习下二叉树。

什么是二叉树 Binary Tree

先来个定义：

二叉树是有限个节点的集合，这个集合可以是空集，也可以是一个根节点和至多两个子二叉树组成的集合，其中一颗树叫做根的左子树，另一棵叫做根的右子树。

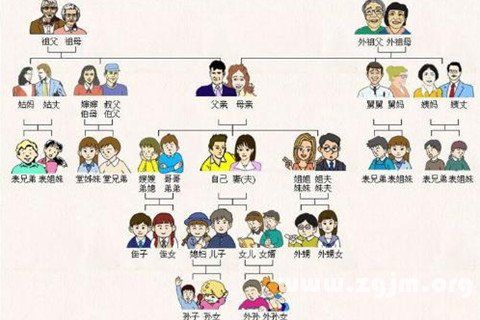
简单地说，二叉树是每个节点至多有两个子树的树，下面的家谱就是一个形象的二叉树：

二叉树的定义是一个递归的定义，其中值得注意的是左右子树的概念，因为有左、右之分，下面两棵树并不是同样的二叉树：

两种特殊的二叉树

有两种特殊的二叉树：

• 满二叉树
• 完全二叉树

满二叉树

在上文 树及 Java 实现 中我们介绍了 树的高度 的定义，而这里 满二叉树 的定义是：

如果一棵树的高度为 k,且拥有 2^k-1 个节点，则称之为 满二叉树。

什么意思呢？

就是说，每个节点要么必须有两棵子树，要么没有子树。

完全二叉树

完全二叉树是一种特殊的二叉树，满足以下要求：

1. 所有叶子节点都出现在 k 或者 k-1 层，而且从 1 到 k-1 层必须达到最大节点数；
2. 第 k 层可是不是慢的，但是第 k 层的所有节点必须集中在最左边。

简单地说，
就是叶子节点都必须在最后一层或者倒数第二层，而且必须在左边。任何一个节点都不能没有左子树却有右子树。

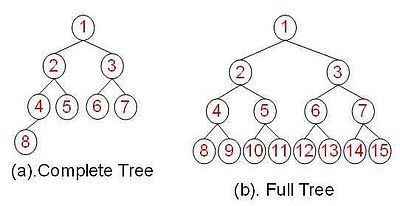
满二叉树 和 完全二叉树 的对比图

来一张图对比下两者：

二叉树的实现

二叉树的实现比普通树简单，因为它最多只有两个节点嘛。

用 递归节点实现法/左右链表示法 表示一个二叉树节点

public class BinaryTreeNode {
    /*
     * 一个二叉树包括 数据、左右孩子 三部分
     */
    private int mData;
    private BinaryTreeNode mLeftChild;
    private BinaryTreeNode mRightChild;

    public BinaryTreeNode(int data, BinaryTreeNode leftChild, BinaryTreeNode rightChild) {
        mData = data;
        mLeftChild = leftChild;
        mRightChild = rightChild;
    }

    public int getData() {
        return mData;
    }

    public void setData(int data) {
        mData = data;
    }

    public BinaryTreeNode getLeftChild() {
        return mLeftChild;
    }

    public void setLeftChild(BinaryTreeNode leftChild) {
        mLeftChild = leftChild;
    }

    public BinaryTreeNode getRightChild() {
        return mRightChild;
    }

    public void setRightChild(BinaryTreeNode rightChild) {
        mRightChild = rightChild;
    }
}

用这种实现方式表示的节点创建的树，结构如右图所示：

用 数组下标表示法 表示一个节点

public class BinaryTreeArrayNode {
    /**
     * 数组实现，保存的不是 左右子树的引用，而是数组下标
     */
    private int mData;
    private int mLeftChild;
    private int mRightChild;

    public int getData() {
        return mData;
    }

    public void setData(int data) {
        mData = data;
    }

    public int getLeftChild() {
        return mLeftChild;
    }

    public void setLeftChild(int leftChild) {
        mLeftChild = leftChild;
    }

    public int getRightChild() {
        return mRightChild;
    }

    public void setRightChild(int rightChild) {
        mRightChild = rightChild;
    }
}

一般使用左右链表示的节点来构造二叉树。

二叉树的主要方法

有了节点后接下来开始构造一个二叉树，二叉树的主要方法有：

• 创建
• 添加元素
• 删除元素
• 清空
• 遍历
• 获得树的高度
• 获得树的节点数
• 返回某个节点的父亲节点
• …

1.二叉树的创建

创建一个二叉树很简单，只需要有一个 二叉根节点，然后提供设置根节点的方法即可：

public class BinaryTree {
    private BinaryTreeNode mRoot;   //根节点

    public BinaryTree() {
    }

    public BinaryTree(BinaryTreeNode root) {
        mRoot = root;
    }

    public BinaryTreeNode getRoot() {
        return mRoot;
    }

    public void setRoot(BinaryTreeNode root) {
        mRoot = root;
    }
}       

2.二叉树的添加元素

由于二叉树有左右子树之分，所以添加元素时也分为两种情况：添加为左子树还是右子树：

 public void insertAsLeftChild(BinaryTreeNode child){
        checkTreeEmpty();
        mRoot.setLeftChild(child);
    }

    public void insertAsRightChild(BinaryTreeNode child){
        checkTreeEmpty();
        mRoot.setRightChild(child);
    }

    private void checkTreeEmpty() {
        if (mRoot == null){
            throw new IllegalStateException("Can't insert to a null tree! Did you forget set value for root?");
        }
    }

在每次插入前都会检查 根节点是否为空，如果是就抛出异常（跟 Android 源码学的嘿嘿）。

3.二叉树的删除元素

删除某个元素很简单，只需要把自己设为 null。

但是为了避免浪费无用的内存，方便 GC 及时回收，我们还需要遍历这个元素的左右子树，挨个设为空：

public void deleteNode(BinaryTreeNode node){
    checkTreeEmpty();
    if (node == null){  //递归出口
        return;
    }
    deleteNode(node.getLeftChild());
    deleteNode(node.getRightChild());
    node = null;
}

4.二叉树的清空

二叉树的清空其实就是特殊的删除元素–删除根节点，因此很简单：

public void clear(){
    if (mRoot != null){
        deleteNode(mRoot);
    }
}

5.获得二叉树的高度

二叉树中，树的高度是 各个节点度的最大值。

因此获得树的高度需要递归获取所有节点的高度，然后取最大值。

   /**
     * 获取树的高度 ，特殊的获得节点高度
     * @return
     */
    public int getTreeHeight(){
        return getHeight(mRoot);
    }
    /**
     * 获得指定节点的度
     * @param node
     * @return
     */
    public int getHeight(BinaryTreeNode node){
        if (node == null){      //递归出口
            return 0;
        }
        int leftChildHeight = getHeight(node.getLeftChild());
        int rightChildHeight = getHeight(node.getRightChild());

        int max = Math.max(leftChildHeight, rightChildHeight);

        return max + 1; //加上自己本身
    }

6.获得二叉树的节点数

获得二叉树的节点数，需要遍历所有子树，然后加上总和。

public int getSize(){
    return getChildSize(mRoot);
}

/**
 * 获得指定节点的子节点个数
 * @param node
 * @return
 */
public int getChildSize(BinaryTreeNode node){
    if (node == null){
        return 0;
    }
    int leftChildSize = getChildSize(node.getLeftChild());
    int rightChildSize = getChildSize(node.getRightChild());

    return leftChildSize + rightChildSize + 1;
}

7.获得某个节点的父亲节点

由于我们使用左右子树表示的节点，不含有父亲节点引用，因此有时候可能也需要一个方法，返回二叉树中，指定节点的父亲节点。

需要从顶向下遍历各个子树，若该子树的根节点的孩子就是目标节点，返回该节点，否则递归遍历它的左右子树：

/**
 * 获得指定节点的父亲节点
 * @param node
 * @return
 */
public BinaryTreeNode getParent(BinaryTreeNode node) {
    if (mRoot == null || mRoot == node) {   //如果是空树，或者这个节点就是根节点，返回空
        return null;
    } else {
        return getParent(mRoot, node);  //否则递归查找 父亲节点
    }
}

/**
 * 递归对比 节点的孩子节点 与 指定节点 是否一致
 *
 * @param subTree 子二叉树根节点
 * @param node    指定节点
 * @return
 */
public BinaryTreeNode getParent(BinaryTreeNode subTree, BinaryTreeNode node) {
    if (subTree == null) {       //如果子树为空，则没有父亲节点，递归出口 1
        return null;
    }
    //正好这个根节点的左右孩子之一与目标节点一致
    if (subTree.getLeftChild() == node || subTree.getRightChild() == node) {    //递归出口 2
        return subTree;
    }
    //需要遍历这个节点的左右子树
    BinaryTreeNode parent;
    if ((parent = getParent(subTree.getLeftChild(), node)) != null) { //左子树节点就是指定节点，返回
        return parent;
    } else {
        return getParent(subTree.getRightChild(), node);    //从右子树找找看
    }

}

二叉树的遍历

二叉树的遍历单独介绍，是因为太重要了！以前考试就老考这个。

前面的那些操作可以发现，二叉树的递归数据结构使得很多操作都可以使用递归进行。

而二叉树的遍历其实也是个 递归遍历的过程，使得每个节点被访问且仅访问一次。

根据不同的场景中，根节点、左右子树遍历的顺序，二叉树的遍历分为三种：

• 先序遍历
• 中序遍历
• 后序遍历

这里先序、中序、后序指的是 根节点相对左右子树的遍历顺序。

先序遍历

即根节点在左右子树之前遍历：

• 先访问根节点
• 再先序遍历左子树
• 再先序遍历右子树
• 退出

代码：

/**
 * 先序遍历
 * @param node
 */
public void iterateFirstOrder(BinaryTreeNode node){
    if (node == null){
        return;
    }
    operate(node);
    iterateFirstOrder(node.getLeftChild());
    iterateFirstOrder(node.getRightChild());
}

/**
 * 模拟操作
 * @param node
 */
public void operate(BinaryTreeNode node){
    if (node == null){
        return;
    }
    System.out.println(node.getData());
}

中序遍历

遍历顺序：

• 先中序遍历左子树
• 再访问根节点
• 再中序遍历右子树
• 退出

代码：

/**
 * 中序遍历
 * @param node
 */
public void iterateMediumOrder(BinaryTreeNode node){
    if (node == null){
        return;
    }
    iterateMediumOrder(node.getLeftChild());
    operate(node);
    iterateMediumOrder(node.getRightChild());
}

后序遍历

即根节点在左右子树之后遍历：

• 先后序遍历左子树
• 再后序遍历右子树
• 最后访问根节点
• 退出

代码：

/**
 * 后序遍历
 * @param node
 */
public void iterateLastOrder(BinaryTreeNode node){
    if (node == null){
        return;
    }
    iterateLastOrder(node.getLeftChild());
    iterateLastOrder(node.getRightChild());
    operate(node);
}

遍历小结

可以看到，三种遍历方式的区别就在于递归的先后。

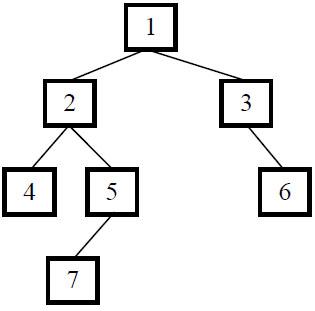
以上图为例，三种遍历结果：

先序遍历：
1 2 4 5 7 3 6

中序遍历：
4 2 7 5 1 3 6

后序遍历：
4 7 5 2 6 3 1

总结

这篇文章介绍了 数据结构中的二叉树的基本概念，常用操作以及三种遍历方式。

其中三种遍历方式一般在面试中可能会考察，给你两种遍历结果，让你画出实际的二叉树结构。只要掌握三种遍历方式的区别，即可解答。

一道笔试题

二叉树遍历

题目描述：

给定一棵二叉树的前序遍历和中序遍历，求其后序遍历（提示：给定前序遍历与中序遍历能够唯一确定后序遍历）。

输入：

两个字符串，其长度n均小于等于26。
第一行为前序遍历，第二行为中序遍历。
二叉树中的结点名称以大写字母表示：A，B，C….最多26个结点。

输出：
输入样例可能有多组，对于每组测试样例，
输出一行，为后序遍历的字符串。

样例输入：

FDXEAG
XDEFAG

样例输出是多少呢？