Java数据结构与算法解析(九)——B树

B树简介

定义

在计算机科学中，B树（英语：B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。

特点

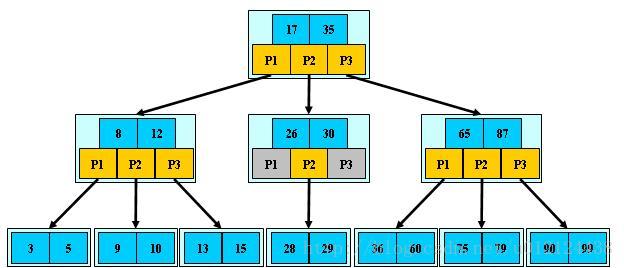
阶为M的B树是一颗具有以下特点的树：
1.数据项存储在树叶上
2.非叶子节点直到M-1个关键字以指示搜索的方向：关键字i代表子树i+1中最小的关键字
3.树的根或者是一片树叶，或者其儿子在2和M之间
4.除根外，所有非树叶节点的儿子数在M/2和M之间。
5.所有的树叶都在相同的深度上并有L/2和L之间个数据项

例如：（M=3）

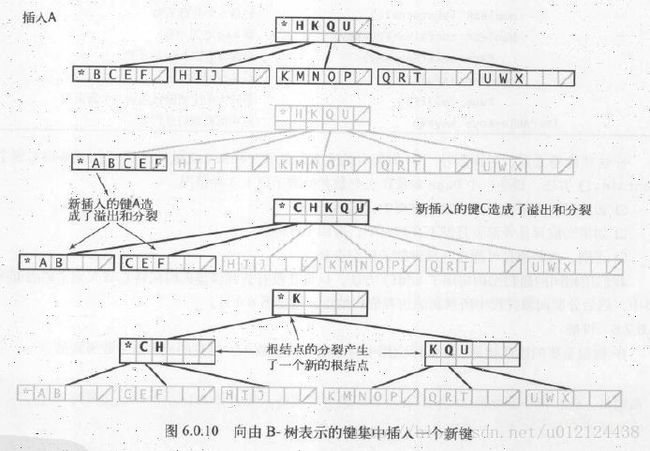
查找和插入

为了方便这里用了一个特殊的哨兵键，它小于其他所有键，用*表示。

一开始B树只含有一个根结点，而根结点在初始化时仅含有该哨兵键。

内部结点中的每个键都与一个结点相关联，以此结点为根的子树种，所有的键都大于等于与此结点关联的键，但小于其他所有键。

B树的实现

public class BTree2<K, V>
{
    private static Log logger = LogFactory.getLog(BTree.class);

    /**
     * B树节点中的键值对。
     * 
 
     * B树的节点中存储的是键值对。
     * 通过键访问值。
     *
     * @param  - 键类型
     * @param  - 值类型
     */
    private static class Entry<K, V>
    {
        private K key;
        private V value;

        public Entry(K k, V v)
        {
            this.key = k;
            this.value = v;
        }

        public K getKey()
        {
            return key;
        }

        public V getValue()
        {
            return value;
        }

        public void setValue(V value)
        {
            this.value = value;
        }

        @Override
        public String toString()
        {
            return key + ":" + value;
        }
    }

    /**
     * 在B树节点中搜索给定键值的返回结果。
     * 
 
     * 该结果有两部分组成。第一部分表示此次查找是否成功，
     * 如果查找成功，第二部分表示给定键值在B树节点中的位置，
     * 如果查找失败，第二部分表示给定键值应该插入的位置。
     */
    private static class SearchResult<V>
    {
        private boolean exist;
        private int index;
        private V value;

        public SearchResult(boolean exist, int index)
        {
            this.exist = exist;
            this.index = index;
        }

        public SearchResult(boolean exist, int index, V value)
        {
            this(exist, index);
            this.value = value;
        }

        public boolean isExist()
        {
            return exist;
        }

        public int getIndex()
        {
            return index;
        }

        public V getValue()
        {
            return value;
        }
    }

    /**
     * B树中的节点。
     *
     * TODO 需要考虑并发情况下的存取。
     */
    private static class BTreeNode<K, V>
    {
        /** 节点的项，按键非降序存放 */
        private List> entrys;
        /** 内节点的子节点 */
        private List> children;
        /** 是否为叶子节点 */
        private boolean leaf;
        /** 键的比较函数对象 */
        private Comparator kComparator;

        private BTreeNode()
        {
            entrys = new ArrayList>();
            children = new ArrayList>();
            leaf = false;
        }

        public BTreeNode(Comparator kComparator)
        {
            this();
            this.kComparator = kComparator;
        }

        public boolean isLeaf()
        {
            return leaf;
        }

        public void setLeaf(boolean leaf)
        {
            this.leaf = leaf;
        }

        /**
         * 返回项的个数。如果是非叶子节点，根据B树的定义，
         * 该节点的子节点个数为({@link #size()} + 1)。
         *
         * @return 关键字的个数
         */
        public int size()
        {
            return entrys.size();
        }

        @SuppressWarnings("unchecked")
        int compare(K key1, K key2)
        {
            return kComparator == null ? ((Comparable)key1).compareTo(key2) : kComparator.compare(key1, key2);
        }

        /**
         * 在节点中查找给定的键。
         * 如果节点中存在给定的键，则返回一个SearchResult，
         * 标识此次查找成功，给定的键在节点中的索引和给定的键关联的值；
         * 如果不存在，则返回SearchResult，
         * 标识此次查找失败，给定的键应该插入的位置，该键的关联值为null。
         * 

         * 如果查找失败，返回结果中的索引域为[0, {@link #size()}]；
         * 如果查找成功，返回结果中的索引域为[0, {@link #size()} - 1]
         * 

         * 这是一个二分查找算法，可以保证时间复杂度为O(log(t))。
         *
         * @param key - 给定的键值
         * @return - 查找结果
         */
        public SearchResult searchKey(K key)
        {
            int low = 0;
            int high = entrys.size() - 1;
            int mid = 0;
            while(low <= high)
            {
                mid = (low + high) / 2; // 先这么写吧，BTree实现中，l+h不可能溢出
                Entry entry = entrys.get(mid);
                if(compare(entry.getKey(), key) == 0) // entrys.get(mid).getKey() == key
                    break;
                else if(compare(entry.getKey(), key) > 0) // entrys.get(mid).getKey() > key
                    high = mid - 1;
                else // entry.get(mid).getKey() < key
                    low = mid + 1;
            }
            boolean result = false;
            int index = 0;
            V value = null;
            if(low <= high) // 说明查找成功
            {
                result = true;
                index = mid; // index表示元素所在的位置
                value = entrys.get(index).getValue();
            }
            else
            {
                result = false;
                index = low; // index表示元素应该插入的位置
            }
            return new SearchResult(result, index, value);
        }

        /**
         * 将给定的项追加到节点的末尾，
         * 你需要自己确保调用该方法之后，节点中的项还是
         * 按照关键字以非降序存放。
         *
         * @param entry - 给定的项
         */
        public void addEntry(Entry entry)
        {
            entrys.add(entry);
        }

        /**
         * 删除给定索引的entry。
         * 

         * 你需要自己保证给定的索引是合法的。
         *
         * @param index - 给定的索引
         * @param 给定索引处的项
         */
        public Entry removeEntry(int index)
        {
            return entrys.remove(index);
        }

        /**
         * 得到节点中给定索引的项。
         * 

         * 你需要自己保证给定的索引是合法的。
         *
         * @param index - 给定的索引
         * @return 节点中给定索引的项
         */
        public Entry entryAt(int index)
        {
            return entrys.get(index);
        }

        /**
         * 如果节点中存在给定的键，则更新其关联的值。
         * 否则插入。
         *
         * @param entry - 给定的项
         * @return null，如果节点之前不存在给定的键，否则返回给定键之前关联的值
         */
        public V putEntry(Entry entry)
        {
            SearchResult result = searchKey(entry.getKey());
            if(result.isExist())
            {
                V oldValue = entrys.get(result.getIndex()).getValue();
                entrys.get(result.getIndex()).setValue(entry.getValue());
                return oldValue;
            }
            else
            {
                insertEntry(entry, result.getIndex());
                return null;
            }
        }

        /**
         * 在该节点中插入给定的项，
         * 该方法保证插入之后，其键值还是以非降序存放。
         * 

         * 不过该方法的时间复杂度为O(t)。
         * 

         * 注意：B树中不允许键值重复。
         *
         * @param entry - 给定的键值
         * @return true，如果插入成功，false，如果插入失败
         */
        public boolean insertEntry(Entry entry)
        {
            SearchResult result = searchKey(entry.getKey());
            if(result.isExist())
                return false;
            else
            {
                insertEntry(entry, result.getIndex());
                return true;
            }
        }

        /**
         * 在该节点中给定索引的位置插入给定的项，
         * 你需要自己保证项插入了正确的位置。
         *
         * @param key - 给定的键值
         * @param index - 给定的索引
         */
        public void insertEntry(Entry entry, int index)
        {
            /*
             * 通过新建一个ArrayList来实现插入真的很恶心，先这样吧
             * 要是有类似C中的reallocate就好了。
             */
            List> newEntrys = new ArrayList>();
            int i = 0;
            // index = 0或者index = keys.size()都没有问题
            for(; i < index; ++ i)
                newEntrys.add(entrys.get(i));
            newEntrys.add(entry);
            for(; i < entrys.size(); ++ i)
                newEntrys.add(entrys.get(i));
            entrys.clear();
            entrys = newEntrys;
        }

        /**
         * 返回节点中给定索引的子节点。
         * 

         * 你需要自己保证给定的索引是合法的。
         *
         * @param index - 给定的索引
         * @return 给定索引对应的子节点
         */
        public BTreeNode childAt(int index)
        {
            if(isLeaf())
                throw new UnsupportedOperationException("Leaf node doesn't have children.");
            return children.get(index);
        }

        /**
         * 将给定的子节点追加到该节点的末尾。
         *
         * @param child - 给定的子节点
         */
        public void addChild(BTreeNode child)
        {
            children.add(child);
        }

        /**
         * 删除该节点中给定索引位置的子节点。
         * 
         * 你需要自己保证给定的索引是合法的。
         *
         * @param index - 给定的索引
         */
        public void removeChild(int index)
        {
            children.remove(index);
        }

        /**
         * 将给定的子节点插入到该节点中给定索引
         * 的位置。
         *
         * @param child - 给定的子节点
         * @param index - 子节点带插入的位置
         */
        public void insertChild(BTreeNode child, int index)
        {
            List> newChildren = new ArrayList>();
            int i = 0;
            for(; i < index; ++ i)
                newChildren.add(children.get(i));
            newChildren.add(child);
            for(; i < children.size(); ++ i)
                newChildren.add(children.get(i));
            children = newChildren;
        }
    }

    private static final int DEFAULT_T = 2;

    /** B树的根节点 */
    private BTreeNode root;
    /** 根据B树的定义，B树的每个非根节点的关键字数n满足(t - 1) <= n <= (2t - 1) */
    private int t = DEFAULT_T;
    /** 非根节点中最小的键值数 */
    private int minKeySize = t - 1;
    /** 非根节点中最大的键值数 */
    private int maxKeySize = 2*t - 1;
    /** 键的比较函数对象 */
    private Comparator kComparator;

    /**
     * 构造一颗B树，键值采用采用自然排序方式
     */
    public BTree()
    {
        root = new BTreeNode();
        root.setLeaf(true);
    }

    public BTree(int t)
    {
        this();
        this.t = t;
        minKeySize = t - 1;
        maxKeySize = 2*t - 1;
    }

    /**
     * 以给定的键值比较函数对象构造一颗B树。
     *
     * @param kComparator - 键值的比较函数对象
     */
    public BTree(Comparator kComparator)
    {
        root = new BTreeNode(kComparator);
        root.setLeaf(true);
        this.kComparator = kComparator;
    }

    public BTree(Comparator kComparator, int t)
    {
        this(kComparator);
        this.t = t;
        minKeySize = t - 1;
        maxKeySize = 2*t - 1;
    }

    @SuppressWarnings("unchecked")
    int compare(K key1, K key2)
    {
        return kComparator == null ? ((Comparable)key1).compareTo(key2) : kComparator.compare(key1, key2);
    }

    /**
     * 搜索给定的键。
     *
     * @param key - 给定的键值
     * @return 键关联的值，如果存在，否则null
     */
    public V search(K key)
    {
        return search(root, key);
    }

    /**
     * 在以给定节点为根的子树中，递归搜索
     * 给定的key
     *
     * @param node - 子树的根节点
     * @param key - 给定的键值
     * @return 键关联的值，如果存在，否则null
     */
    private V search(BTreeNode node, K key)
    {
        SearchResult result = node.searchKey(key);
        if(result.isExist())
            return result.getValue();
        else
        {
            if(node.isLeaf())
                return null;
            else
                search(node.childAt(result.getIndex()), key);

        }
        return null;
    }

    /**
     * 分裂一个满子节点childNode。
     * 

     * 你需要自己保证给定的子节点是满节点。
     *
     * @param parentNode - 父节点
     * @param childNode - 满子节点
     * @param index - 满子节点在父节点中的索引
     */
    private void splitNode(BTreeNode parentNode, BTreeNode childNode, int index)
    {
        assert childNode.size() == maxKeySize;

        BTreeNode siblingNode = new BTreeNode(kComparator);
        siblingNode.setLeaf(childNode.isLeaf());
        // 将满子节点中索引为[t, 2t - 2]的(t - 1)个项插入新的节点中
        for(int i = 0; i < minKeySize; ++ i)
            siblingNode.addEntry(childNode.entryAt(t + i));
        // 提取满子节点中的中间项，其索引为(t - 1)
        Entry entry = childNode.entryAt(t - 1);
        // 删除满子节点中索引为[t - 1, 2t - 2]的t个项
        for(int i = maxKeySize - 1; i >= t - 1; -- i)
            childNode.removeEntry(i);
        if(!childNode.isLeaf()) // 如果满子节点不是叶节点，则还需要处理其子节点
        {
            // 将满子节点中索引为[t, 2t - 1]的t个子节点插入新的节点中
            for(int i = 0; i < minKeySize + 1; ++ i)
                siblingNode.addChild(childNode.childAt(t + i));
            // 删除满子节点中索引为[t, 2t - 1]的t个子节点
            for(int i = maxKeySize; i >= t; -- i)
                childNode.removeChild(i);
        }
        // 将entry插入父节点
        parentNode.insertEntry(entry, index);
        // 将新节点插入父节点
        parentNode.insertChild(siblingNode, index + 1);
    }

    /**
     * 在一个非满节点中插入给定的项。
     *
     * @param node - 非满节点
     * @param entry - 给定的项
     * @return true，如果B树中不存在给定的项，否则false
     */
    private boolean insertNotFull(BTreeNode node, Entry entry)
    {
        assert node.size() < maxKeySize;

        if(node.isLeaf()) // 如果是叶子节点，直接插入
            return node.insertEntry(entry);
        else
        {
            /* 找到entry在给定节点应该插入的位置，那么entry应该插入
             * 该位置对应的子树中
             */
            SearchResult result = node.searchKey(entry.getKey());
            // 如果存在，则直接返回失败
            if(result.isExist())
                return false;
            BTreeNode childNode = node.childAt(result.getIndex());
            if(childNode.size() == 2*t - 1) // 如果子节点是满节点
            {
                // 则先分裂
                splitNode(node, childNode, result.getIndex());
                /* 如果给定entry的键大于分裂之后新生成项的键，则需要插入该新项的右边，
                 * 否则左边。
                 */
                if(compare(entry.getKey(), node.entryAt(result.getIndex()).getKey()) > 0)
                    childNode = node.childAt(result.getIndex() + 1);
            }
            return insertNotFull(childNode, entry);
        }
    }

    /**
     * 在B树中插入给定的键值对。
     *
     * @param key - 键
     * @param value - 值
     * @param true，如果B树中不存在给定的项，否则false
     */
    public boolean insert(K key, V value)
    {
        if(root.size() == maxKeySize) // 如果根节点满了，则B树长高
        {
            BTreeNode newRoot = new BTreeNode(kComparator);
            newRoot.setLeaf(false);
            newRoot.addChild(root);
            splitNode(newRoot, root, 0);
            root = newRoot;
        }
        return insertNotFull(root, new Entry(key, value));
    }

    /**
     * 如果存在给定的键，则更新键关联的值，
     * 否则插入给定的项。
     *
     * @param node - 非满节点
     * @param entry - 给定的项
     * @return true，如果B树中不存在给定的项，否则false
     */
    private V putNotFull(BTreeNode node, Entry entry)
    {
        assert node.size() < maxKeySize;

        if(node.isLeaf()) // 如果是叶子节点，直接插入
            return node.putEntry(entry);
        else
        {
            /* 找到entry在给定节点应该插入的位置，那么entry应该插入
             * 该位置对应的子树中
             */
            SearchResult result = node.searchKey(entry.getKey());
            // 如果存在，则更新
            if(result.isExist())
                return node.putEntry(entry);
            BTreeNode childNode = node.childAt(result.getIndex());
            if(childNode.size() == 2*t - 1) // 如果子节点是满节点
            {
                // 则先分裂
                splitNode(node, childNode, result.getIndex());
                /* 如果给定entry的键大于分裂之后新生成项的键，则需要插入该新项的右边，
                 * 否则左边。
                 */
                if(compare(entry.getKey(), node.entryAt(result.getIndex()).getKey()) > 0)
                    childNode = node.childAt(result.getIndex() + 1);
            }
            return putNotFull(childNode, entry);
        }
    }

    /**
     * 如果B树中存在给定的键，则更新值。
     * 否则插入。
     *
     * @param key - 键
     * @param value - 值
     * @return 如果B树中存在给定的键，则返回之前的值，否则null
     */
    public V put(K key, V value)
    {
        if(root.size() == maxKeySize) // 如果根节点满了，则B树长高
        {
            BTreeNode newRoot = new BTreeNode(kComparator);
            newRoot.setLeaf(false);
            newRoot.addChild(root);
            splitNode(newRoot, root, 0);
            root = newRoot;
        }
        return putNotFull(root, new Entry(key, value));
    }

    /**
     * 从B树中删除一个与给定键关联的项。
     *
     * @param key - 给定的键
     * @return 如果B树中存在给定键关联的项，则返回删除的项，否则null
     */
    public Entry delete(K key)
    {
        return delete(root, key);
    }

    /**
     * 从以给定node为根的子树中删除与给定键关联的项。
     * 

     * 删除的实现思想请参考《算法导论》第二版的第18章。
     *
     * @param node - 给定的节点
     * @param key - 给定的键
     * @return 如果B树中存在给定键关联的项，则返回删除的项，否则null
     */
    private Entry delete(BTreeNode node, K key)
    {
        // 该过程需要保证，对非根节点执行删除操作时，其关键字个数至少为t。
        assert node.size() >= t || node == root;

        SearchResult result = node.searchKey(key);
        /*
         * 因为这是查找成功的情况，0 <= result.getIndex() <= (node.size() - 1)，
         * 因此(result.getIndex() + 1)不会溢出。
         */
        if(result.isExist())
        {
            // 1.如果关键字在节点node中，并且是叶节点，则直接删除。
            if(node.isLeaf())
                return node.removeEntry(result.getIndex());
            else
            {
                // 2.a 如果节点node中前于key的子节点包含至少t个项
                BTreeNode leftChildNode = node.childAt(result.getIndex());
                if(leftChildNode.size() >= t)
                {
                    // 使用leftChildNode中的最后一个项代替node中需要删除的项
                    node.removeEntry(result.getIndex());
                    node.insertEntry(leftChildNode.entryAt(leftChildNode.size() - 1), result.getIndex());
                    // 递归删除左子节点中的最后一个项
                    return delete(leftChildNode, leftChildNode.entryAt(leftChildNode.size() - 1).getKey());
                }
                else
                {
                    // 2.b 如果节点node中后于key的子节点包含至少t个关键字
                    BTreeNode rightChildNode = node.childAt(result.getIndex() + 1);
                    if(rightChildNode.size() >= t)
                    {
                        // 使用rightChildNode中的第一个项代替node中需要删除的项
                        node.removeEntry(result.getIndex());
                        node.insertEntry(rightChildNode.entryAt(0), result.getIndex());
                        // 递归删除右子节点中的第一个项
                        return delete(rightChildNode, rightChildNode.entryAt(0).getKey());
                    }
                    else // 2.c 前于key和后于key的子节点都只包含t-1个项
                    {
                        Entry deletedEntry = node.removeEntry(result.getIndex());
                        node.removeChild(result.getIndex() + 1);
                        // 将node中与key关联的项和rightChildNode中的项合并进leftChildNode
                        leftChildNode.addEntry(deletedEntry);
                        for(int i = 0; i < rightChildNode.size(); ++ i)
                            leftChildNode.addEntry(rightChildNode.entryAt(i));
                        // 将rightChildNode中的子节点合并进leftChildNode，如果有的话
                        if(!rightChildNode.isLeaf())
                        {
                            for(int i = 0; i <= rightChildNode.size(); ++ i)
                                leftChildNode.addChild(rightChildNode.childAt(i));
                        }
                        return delete(leftChildNode, key);
                    }
                }
            }
        }
        else
        {
            /*
             * 因为这是查找失败的情况，0 <= result.getIndex() <= node.size()，
             * 因此(result.getIndex() + 1)会溢出。
             */
            if(node.isLeaf()) // 如果关键字不在节点node中，并且是叶节点，则什么都不做，因为该关键字不在该B树中
            {
                logger.info("The key: " + key + " isn't in this BTree.");
                return null;
            }
            BTreeNode childNode = node.childAt(result.getIndex());
            if(childNode.size() >= t) // // 如果子节点有不少于t个项，则递归删除
                return delete(childNode, key);
            else // 3
            {
                // 先查找右边的兄弟节点
                BTreeNode siblingNode = null;
                int siblingIndex = -1;
                if(result.getIndex() < node.size()) // 存在右兄弟节点
                {
                    if(node.childAt(result.getIndex() + 1).size() >= t)
                    {
                        siblingNode = node.childAt(result.getIndex() + 1);
                        siblingIndex = result.getIndex() + 1;
                    }
                }
                // 如果右边的兄弟节点不符合条件，则试试左边的兄弟节点
                if(siblingNode == null)
                {
                    if(result.getIndex() > 0) // 存在左兄弟节点
                    {
                        if(node.childAt(result.getIndex() - 1).size() >= t)
                        {
                            siblingNode = node.childAt(result.getIndex() - 1);
                            siblingIndex = result.getIndex() - 1;
                        }
                    }
                }
                // 3.a 有一个相邻兄弟节点至少包含t个项
                if(siblingNode != null)
                {
                    if(siblingIndex < result.getIndex()) // 左兄弟节点满足条件
                    {
                        childNode.insertEntry(node.entryAt(siblingIndex), 0);
                        node.removeEntry(siblingIndex);
                        node.insertEntry(siblingNode.entryAt(siblingNode.size() - 1), siblingIndex);
                        siblingNode.removeEntry(siblingNode.size() - 1);
                        // 将左兄弟节点的最后一个孩子移到childNode
                        if(!siblingNode.isLeaf())
                        {
                            childNode.insertChild(siblingNode.childAt(siblingNode.size()), 0);
                            siblingNode.removeChild(siblingNode.size());
                        }
                    }
                    else // 右兄弟节点满足条件
                    {
                        childNode.insertEntry(node.entryAt(result.getIndex()), childNode.size() - 1);
                        node.removeEntry(result.getIndex());
                        node.insertEntry(siblingNode.entryAt(0), result.getIndex());
                        siblingNode.removeEntry(0);
                        // 将右兄弟节点的第一个孩子移到childNode
                        // childNode.insertChild(siblingNode.childAt(0), childNode.size() + 1);
                        if(!siblingNode.isLeaf())
                        {
                            childNode.addChild(siblingNode.childAt(0));
                            siblingNode.removeChild(0);
                        }
                    }
                    return delete(childNode, key);
                }
                else // 3.b 如果其相邻左右节点都包含t-1个项
                {
                    if(result.getIndex() < node.size()) // 存在右兄弟，直接在后面追加
                    {
                        BTreeNode rightSiblingNode = node.childAt(result.getIndex() + 1);
                        childNode.addEntry(node.entryAt(result.getIndex()));
                        node.removeEntry(result.getIndex());
                        node.removeChild(result.getIndex() + 1);
                        for(int i = 0; i < rightSiblingNode.size(); ++ i)
                            childNode.addEntry(rightSiblingNode.entryAt(i));
                        if(!rightSiblingNode.isLeaf())
                        {
                            for(int i = 0; i <= rightSiblingNode.size(); ++ i)
                                childNode.addChild(rightSiblingNode.childAt(i));
                        }
                    }
                    else // 存在左节点，在前面插入
                    {
                        BTreeNode leftSiblingNode = node.childAt(result.getIndex() - 1);
                        childNode.insertEntry(node.entryAt(result.getIndex() - 1), 0);
                        node.removeEntry(result.getIndex() - 1);
                        node.removeChild(result.getIndex() - 1);
                        for(int i = leftSiblingNode.size() - 1; i >= 0; -- i)
                            childNode.insertEntry(leftSiblingNode.entryAt(i), 0);
                        if(!leftSiblingNode.isLeaf())
                        {
                            for(int i = leftSiblingNode.size(); i >= 0; -- i)
                                childNode.insertChild(leftSiblingNode.childAt(i), 0);
                        }
                    }
                    // 如果node是root并且node不包含任何项了
                    if(node == root && node.size() == 0)
                        root = childNode;
                    return delete(childNode, key);
                }
            }
        }
    }

    /**
     * 一个简单的层次遍历B树实现，用于输出B树。
     */
    public void output()
    {
        Queue> queue = new LinkedList>();
        queue.offer(root);
        while(!queue.isEmpty())
        {
            BTreeNode node = queue.poll();
            for(int i = 0; i < node.size(); ++ i)
                System.out.print(node.entryAt(i) + " ");
            System.out.println();
            if(!node.isLeaf())
            {
                for(int i = 0; i <= node.size(); ++ i)
                    queue.offer(node.childAt(i));
            }
        }
    }

    public static void main(String[] args)
    {
        Random random = new Random();
        BTree2 btree = new BTree2(3);
        List save = new ArrayList();
        for(int i = 0; i < 10; ++ i)
        {
            int r = random.nextInt(100);
            save.add(r);
            System.out.println(r);
            btree.insert(r, r);
        }

        System.out.println("----------------------");
        btree.output();
        System.out.println("----------------------");
        btree.delete(save.get(0));
        btree.output();
    }
}