KGAT : Knowledge Graph Attention Network for Recommendation 用于推荐的知识图注意力网络 KDD2019

论文来源：KDD 2019
论文链接
代码及数据集链接

1、摘要

在推荐系统领域中，为了使推荐结果更加准确、可解释性更高，不仅要考虑user-item之间的关系，引入外部知识丰富user-item之间的信息也非常有必要。在这方面比较常用的方法主要有FM算法（factorization machine，因子分解机），该方法主要问题在于将user-item作为相互独立的实例，忽视了item之间可能存在的相互作用关系。

本文提出了一种基于知识图谱和注意力机制的新方法-KGAT（Knowledge Graph Attention Network）。该方法通过user和item之间的属性将user-item实例链接在一起，摒弃user-item之间相互独立的假设。该方法将user-item和知识图谱融合在一起形成一种新的网络结构，并从该网络结构中抽取高阶链接路径用来表达网络中的节点。

2、背景

常用推荐算法主要有CF算法（collaborative filtering）和SL算法（supervised learning）。

协同过滤的模型一般为m个物品，n个用户的数据，只有部分用户和部分数据之间是有评分数据的，其它部分评分是空白，此时我们要用已有的部分稀疏数据来预测那些空白的物品和数据之间的评分关系，找到最高评分的物品推荐给用户。

一般来说，协同过滤推荐分为三种类型。第一种是基于用户(user-based)的协同过滤，第二种是基于项目(item-based)的协同过滤，第三种是基于模型(model based)的协同过滤。基于模型(model based)的协同过滤是目前最主流的协同过滤类型了，我们的一大堆机器学习算法也可以在这里找到用武之地。

基于用户的CF(User-Based CF主要思想是利用的打分矩阵, 利用统计信息计算用户和用户, item和item之间的相似度。然后再利用相似度排序, 最终得出推荐结果。
在协同过滤中，一个重要的环节就是如何选择合适的相似度计算方法，常用的两种相似度计算方法包括皮尔逊相关系数和余弦相似度等。皮尔逊相关系数的计算公式为：

根据皮尔逊公式，基于用户的CF算法公式为：

该公式要计算用户$i$和用户$j$之间的相似度, $I_{ij}$是代表用户i和用户j共同评价过的物品, $R(i,x)$代表用户i对物品$x$的评分, $\overline{R(i)}$代表用户$i$所有评分的平均分:之所以要减去平均分是因为有的用户打分严有的松, 归一化用户打分避免相互影响。

基于项目的CF(Item-Based CF) 和基于用户的CF类似，只不过这时我们要求物品和物品之间的相似度，就先要找到（或获得）目标用户对某些物品的评分，那么我们就可以对相似度高的类似物品进行预测，将评分最高的若干个相似物品推荐给用户。比如你在网上买了一本机器学习相关的书，网站马上会推荐一堆机器学习，大数据相关的书给你，这里就明显用到了基于项目的协同过滤思想。
既然IBCF和UBCF是类似的，那就可以借鉴UBCF的思想，选一个合适的相似度呗——所以还可以用皮尔逊，最终得到IBCF公式：

我们从上面最最最传统的CF公式（好吧或者说是算法）可以看出它面临两个问题：

• 矩阵稀疏问题
• 计算资源有限导致的可扩展性不好

协同过滤CF算法利用用户的行为信息进行偏好预测，该方法在推荐系统里有较好的应用。但是CF算法不能对其他信息（比如商品的属性、用户信息、上文下）进行建模，而且在用户-商品交互信息较少的数据上表现较差。
为了能把其他信息利用起来，学术界常用的做法是：将用户跟商品都用embedding向量进行表示，然后将他们输入监督学习的模型里训练，将用户表示与商品表示的相关性作为训练目标。这里相关工作有：factorization machine (FM) [7], NFM (neural FM) [6], Wide&Deep [5], DCN[4],and xDeepFM [3]等。

扩展一下（加点小菜）：

FM:在线性回归的基础上加入二阶线性特征。 $y=w_0+{\sum }_{i=1}^n{w}_i{x}_i+{\sum }_{i=1}^n{\sum }_{j=i+1}^n{w}_{ij}{x}_i{x}_j$，优点：考虑二阶特征之间的相互作用。缺点：仅仅考虑线性特征，没有加入非线性特征。

NFM：融合了FM提取二阶线性特征与神经网络提取高阶非线性特征的两者优点。$y=w_0+{\sum }_{i=1}^n{w}_i{x}_i+f(x)$,其中$f(x)$是用神经网络对输入特征$x$进行特征抽取建模。

Wide&Deep:模型包括两个部分，分别为Wide部分和Deep部分，Wide部分如图1的左图所示，Deep部分如下图中的右图所示。Wide模型就是一个广义线性模型，Wide模型是前馈神经网络。两种模型进行联合训练，将两个模型的结果加权求和作为最终的预测结果。

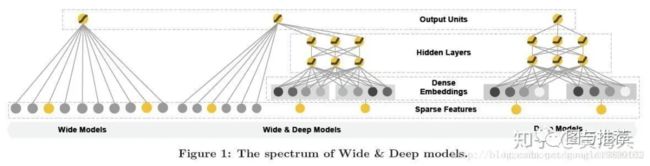
虽然这些模型都能取得不错的效果，但是这些模型有个缺点：将训练数据里（用户交互数据）的特征进行独立建模，没有考虑到交互数据之间的关系。这使得这些模型不足以从用户的行为中提取出基于属性的协同信息。

比如下图2中，用户u1看了电影 i1，这个电影是e1导演的，传统的CF方法会着重去找那些也看了电影i1的用户，比如u4跟u5。而监督学习方法会重点关注那些有相同属性e1的电影，比如i2。很显然这两类信息都可以作为推荐信息的补充，但是现有的模型不能做到上面两者信息的融合，而且这里的高阶关系也可以作为推荐信息的补充的。比如图中黄色框图里的用户看了同样由e1导演的电影i2, 还有灰色框图里电影同样也有e1的参与。

为了解决上面提到的问题，本文提出 collaborative knowledge graph (CKG)方法，将图谱关系信息及用户user点击商品item的交互图融合到一个图空间里。这样就可以融合CF信息及KG信息，同时也可以通过CKG发现高阶的关系信息。

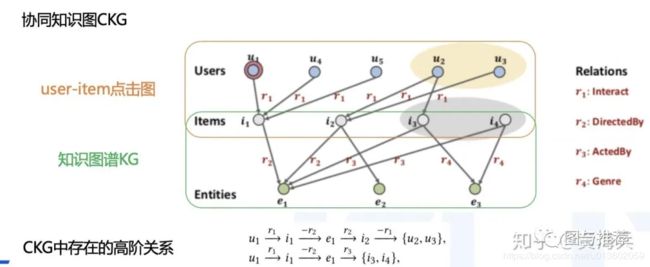
作者认为，成功推荐的关键在于充分利用CKG图的高阶关系，比如这种(能够到达SL所及不了的黄圈和灰圈)远程连通性：

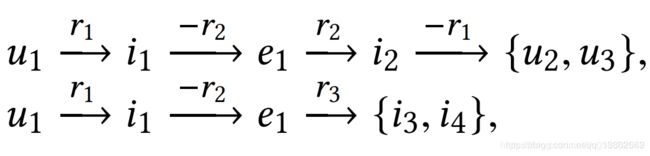
那么，怎么使用图模型来实现呢？考虑怎么实现，就要分析需要克服什么问题：

• 与目标用户具有高阶关系的节点随着阶数的增加而急剧增加，给模型增加了计算负荷（也就是为后文embedding layer做铺垫）
• 高阶关系对预测的贡献是不均衡的，这就要求模型仔细地权衡(或选择)它们（也就是为后文Attention引入的权值矩阵做铺垫）

本文的贡献：

1. 强调了在CKG中显式建模高阶关系信息的重要性，以便提供更多信息的用于推荐。
2. 提出来一种新的推荐方法KGAT，该方法在图神经网络框架下以显式且端到端的方式实现了高阶关系的建模。
3. 我们在三个公开基准上进行了大量实验，证明了KGAT的有效性及其在理解高级关系重要性方面的可解释性。

3、任务描述

3.1、User-Item Bipartite Graph

还是以看电影为例：用户(user)和电影(items)之间是有历史交互信息的，比如你们以前看过XXXX电影。那么我们把这个interaction data做成一个用户-项目的双边关系图$G_1$，定义：
$$G_1=\{(u,y_{ui},i)|u\in U,i\in I\}$$其中$U$和$I$表示用户和项目的集合，连接$y_{ui}=1$代表观察到集合中某一个$u$和某一个$i$出现交互，反之为0。

3.2、knowledge Graph

针对3.1中的这个交互interactions，我们可以从中的得到项目的附加信息(side information)，比如电影的属性和外部知识（啥是外部知识？可以理解为比如一部电影的emmmm历史背景?_？）。通常这些辅助数据可以从真实世界的实体(电影导演)和它们之间的关系获得，进而组成一个电影(item)

比如形容一部电影可以从它的导演，灯光师，流派风格等等着手。那么我们把这些side information做成“由实体-属性-另一个对应的实体”三元组构成的有向图$G_2$：
$$G_2=\{(h,r,t)|h,t\in \xi ,r\in R\}$$其中每一个三元组表示一个从头实体$h$到尾实体$t$的双向关系（怎么理解？）

比如三元组 (Altria ActorOf Saber）代表在《命运之夜天之杯》电影中："人物阿尔托莉雅是角色Saber的饰演者"这层关系;而我们也可以表示成 (Saber ActorIn Altria）表明Saber的饰演者是型月著名女一号阿尔托莉雅小姐。然而无论是Saber还是阿尔托莉雅都不是用户user，这也就是说这个G2能囊括很多电影相关的信息。

然而作者并非止步于谁是Saber谁是Fate这个深度，作者希望把老虚也拉进来，于是建立了"item-entity alignments"这层关系：
$$A=\{(i,e)|i\in I,e\in \xi \}$$从而拓宽了模型的深度（喜欢老虚的可能就能推荐Fate/Zero）

3.3、Collaborative Knowledge Graph

将用户喜好和电影知识形成统一的关系图，首先要用数学语言表示出“用户喜好”：
$$(u,Interact,i)$$其中，$y_{ui}=1$表示在用户和电影之间有交互关系
基于3.2中后半部分的电影-老虚关系(item-entity)集合的思想，为了拓宽模型深度，作者一统天下，把用户-老虚(user-entity)图和3.2前半部分的KG图$G_2$整合成统一图：
$$G=\{(h,r,t)|h,t\in {\xi }^{\prime },r\in R^{\prime }\}$$其中${\xi }^{\prime }=\xi \bigcup U,R^{\prime }=R\bigcup Interact$
换句话说这段意思就是：

• 对于实体：把用户和Saber、Altria、老虚…等等众多和item有关的因素实体合起来形成的新实体集合${\xi }^{\prime }$。
• 对于关系：将用户（用户只是众多实体中的一种实体）与电影的单向交互关系InteractInteractInteract和多种其他实体的双向关系结合起来，得到新关系集合$R^{\prime }$。

3.4、High-Order Connectivity

作者再次重申了利用高阶连通性是优秀推荐的重要保障，并为我们描述了L阶连通性是什么亚子：
其中上面的$e_i$和$r_i$都来自新实体集合${\xi }^{\prime }$和新关系集合$R^{\prime }$。
上图写作
$$(e_{l-1},r_l,e_l)$$读作第$l$个三元组，并称这个三元组序列的长度为$L$。

至此，我们学习完了基本知识，但是为什么要学习这些知识呢？为啥要把这几个集合合起来呢？我要是不合起来会咋样呢？

不合起来，行，那就走传统路线，CF或者SL模型选一个吧！
好，CF模型的连通性结构长下面这个亚子：

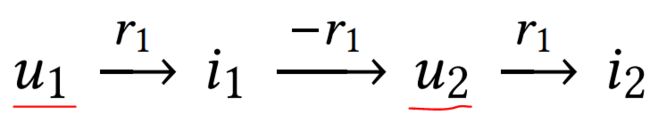
可以看出来，CF方法建立在用户之间行为相似的基础上——更具体地说，相似的用户在项目上表现出相似的偏好。比如，我舍友(u1)喜欢(r1)看《Fate/Zero》，而我(u2)也喜欢看,然后我u2还喜欢看《超炮》，那我把超炮推荐给我舍友u1吗？事实上我舍友只喜欢看老虚这种风格的作品，超炮太治愈了舍友接受不了，所以这种连通不稳。

那换SL算法呢？

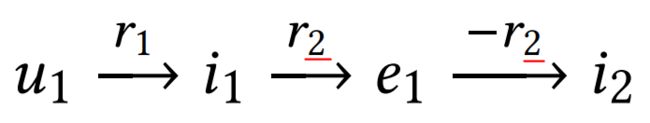
SL算法通常只考虑一个实体的一个特征，也就是说从一部电影到另一部电影只能考虑一个因素，比如上图中的$r_2$这一个因素，无法显示items和相关实例之间的相关性,比如下图这种情况（左边考虑导演喜好关系右边考虑演员喜好关系）就行不通。

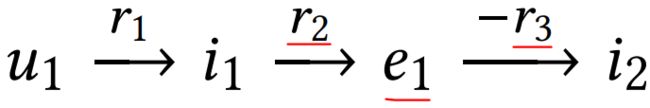
4、模型

本文提出的KGAT模型由以下三个部分组成，嵌入层、注意力嵌入传播层和预测层，这些在图中表示的也很清晰：

4.1、Embedding Layer

为了将数据输入网络中，首先要进行嵌入，这里给自己啰嗦一下啥是图嵌入：

图嵌入是一种将图数据（通常为高维稀疏的矩阵）映射为低微稠密向量的过程。我们都知道图是由节点和边构成，这些向量关系一般只能使用数学，统计或者特定的子集进行表示，但是嵌入之后的向量空间具有更加灵活和丰富的计算方式，方便进行机器学习。

图嵌入能够压缩数据， 我们一般用邻接矩阵描述图中节点之间的连接。 连接矩阵的维度是$|V|\ast |V|$，其中$|V|$是图中节点的个数。矩阵中的每一列和每一行都代表一个节点。矩阵中的非零值表示两个节点已连接。

将一个图embedding成低维稠密向量有两种方法，但这两种方法万变不离其宗的思想就是Word2Vec思想(独热编码后扔到DNN中梯度下降经过Softmax输出选择概率）

• 节点嵌入（以DeepWalk为例）：随机游走起始于选定的节点，然后从当前节点移至随机邻居，并执行一定的步数，该方法大致可分为三个步骤：

1. 采样：通过随机游走对图上的节点进行采样，在给定的时间内得到一个节点构成的序列
2. 训练skip-gram：随机游走得到的节点序列与word2vec方法中的句子相当。文本中skip-gram的输入是一个句子，在这里输入为随机游走采样得到的序列，然后通过最大化预测相邻节点的概率进而学习预测周围节点

• 图嵌入方法：图嵌入是将整个图用一个向量表示的方法，Graph2vec同样由三个步骤构成：

1. 采样并重新标记图中的所有子图。子图是出现在所选节点周围的一组节点。子图中的节点距离所选边数不远。
2. 训练skip-gram模型,类比Word2Vec。经过训练，可以最大程度地预测输入中存在于图中的子图的概率。
3. 通过在输入处提供子图的id索引向量来计算嵌入

那么，咱们分析一下，这里用的是图嵌入还是节点嵌入呢？
我个人的理解是图嵌入，因为从KGAT的模型中从第一步就开始建立子图（三元组，就是图中的$e_{i_1}^0$等subgraph）,毕竟我理解的两种嵌入最大的区别就是是直接刚节点还是曲线救国积沙成塔整合区域节点为子图。

我们嵌入好了，就运用TransR模型：（关于TransR模型可以先简单理解为建立$(h,r,t)$的向量运算关系，是真正的数学层面关系）
$$TransR:e_t^r=e_h^r+e_r$$其中$e_h,e_t\in {\mathbb{R}}^d$代表一个三元组$(h,r,t)$经过嵌入embedding后的头实体和尾实体，$e_r\in {\mathbb{R}}^k$同理。并且上角标$r$表示的是经过TransR变换到$r$超平面中的$e_h,e_t$。

为了解决之前提出的第二个高亮问题（分配不均衡），我们将输入特征转换为高层特征，这一过程需要一个可学习的线性转换（one learnable linear transformation）。为了达到该目标，我们考虑采用《Attention is All You Need》这篇神文的一个共享的线性转换，通过对每一个节点进行加权。我们称这一过程为self-attention。

对于一个给定的三元组，根据《Graph Attention Networks》给出的self-attention处理模型：
回过头针对这里的三个变量模型，我们建立自己的势能函数：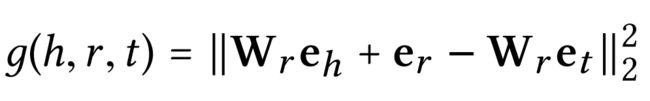
其中$W_r\in {\mathbb{R}}^{k\times d}$是关系$r$的变换矩阵，将${\mathbb{R}}^d$的实体空间转换到${\mathbb{R}}^k$的$r$关系超平面中（这一超平面就是之前TransR过程中的超平面，换言之，若你用TransE就不需要转换）

考虑到损失函数（loss function）是用来估量你模型的预测值$f(x)$与真实值$Y$的不一致程度，它是一个非负实值函数,通常使用$L(Y,f(x))$来表示，损失函数越小，模型的鲁棒性就越好。所以这里我们给出势能函数$g(h,r,t)$的损失函数：

其中$\sigma$是sigmoid函数，自变量趋于正/负无穷时输出1或0。通常我们给正样例的分数高，负样例的分数低，保证括号内作差小于0 （外面一个负号，负负得正）从而保证训练过程每轮Loss大于0。

这里还需要啰嗦一句：$g(h,r,t^{\prime })$和$g(h,r,t)$的关系：前者表示不存在图中的三元组组合。啥意思咧？
咱们训练不是要正负样例吗（在SL基础上改的肯定要监督哇），我们用正样例，比如：(美国 总统 奥巴马) 去生成一个和这个正样例相关的负样例：(美国 总统 本拉登）。但是，万一我们的语料库中正好有拉登这个负样例，那就重复了嘛，所以这里还有专门的处理方法（我忘了，恳请各位大神补充）。

4.2、Attentive Embedding Propagation Layers

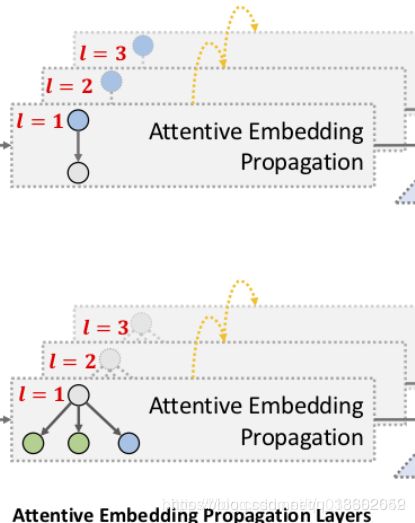
这一节讲的是传播。
我们先从单层的传播描述，然后再介绍从单层到多层的方法。

4.2.1、Information Propagation

一个实体可以包含在多个三元组中，理论上充当连接两个三元组和传播信息的桥梁，比如：

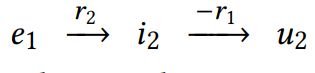
和

这里面$i_2$可以将$e_1$和$e_2$作为输入来enrich自己的特征，从而为用户$u_2$提供更多的选择推荐。这就是我们实现信息传递的中心思想。

考虑实体$h$,我们记"以实体$h$为头实体的所有三元组"为ego-network：

为了刻画实体$h$的一阶连通性结构，我们记$h$的ego-network网络的线性组合为：
其中$\pi (h,r,t)$决定三元组$(h,r,t)$上每次传播的衰减系数，可以理解为从$t$到$h$传播的信息中有多少与$r$有关。

通过公式怎么看出衰减系数依赖于在关系$r$向量空间中尾实体$t$与头实体 $h$的距离，具体这个是怎么理解的？
我的理解是这样的：(这是我在知乎上的回答）
1、 首先，这里的衰减系数π(h,r,t)，就是我们通常attention机制中的计算相似度的第四种方法，而这个π(h,r,t)是怎么来的呢？请看下文
2、 在attention中，我们取一个非线性函数f(比如LeakyReLU就行)表征两个实体之间的相似度(在《Attention is all you need》这篇神文里指的是Q,V,K向量，可以了解一下)。那么我们经过多次迭代所有实体后，需要输出attention向量以计算对应特征的线性加权，所以就需要将得到的相似度进行归一化，就是文中的tanh（第四种）操作。所以这里的衰减系数π(h,r,t)，我谨理解为是相似度的归一化函数。
3、 2中的非线性函数，在这篇文章中就是g(h,r,t)，所以衰减系数π(h,r,t)本质上是g的函数，而g(h,r,t)中是有着h与t的距离信息的。所以衰减系数π(h,r,t)就可能依赖于距离了。

4.2.2、Knowledge-aware Attention

下面这一部分就是Attention中的内容了，注意力函数$e_{ij}$也有很多种变体。四种注意力变体：加性注意力（additive attention）、乘法（点积）注意力（multiplicative attention）、自注意力（self-attention）和关键值注意力（key-value attention）。这里给出的是用tanh非线性激励函数加性注意力（additive attention）,可以使得注意力得分依赖于超平面$r$空间中$e_h$和$e_t$之间的距离，为更近的实体传播更多信息。

我们采用softmax函数对所有与刚刚说的与$h$头实体相连的三元组的系数进行归一化处理:

4.2.3、Information Aggregation

好了我现在得到每一层的输出的概率了，那么现在要把所有层加起来，大概对应于图中的这一步：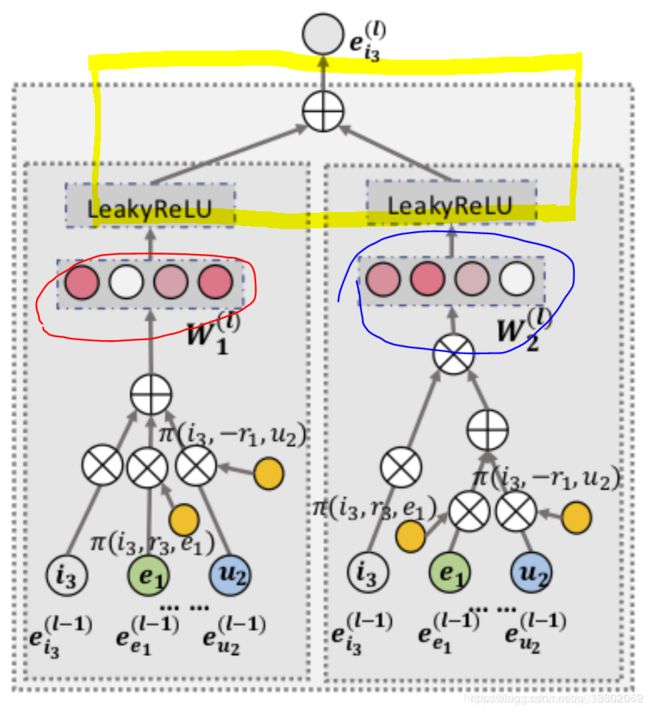
红圈是第一层，蓝圈是第二层，高亮黄框应该延伸到$W_1^l$和$W_2^l$的，这里是我涂鸦失误，误把这里的$W$和之前的$W_r$混淆了。

最后一步首先要完成聚合(aggregation)，这里我们以第一种聚合器为例，《Semi-Supervised Classification with Graph Convolutional Networks》提出的聚合器：输入是两个表示向量的和，然后与可训练权值的$d^{\prime }\times d$矩阵$W$相乘后再经过激活函数(这里取了LeakyReLU)后输出。其中$W$是可以提取有用的信息用于传播的权值矩阵。

4.2.4、High-order Propagation

我们可以进一步堆叠更多的传播层来得到高阶连接信息，收集从高阶邻点的传播信息。在第$l^{th}$步骤中，我们递归地将一个实体的表示形式表示为：

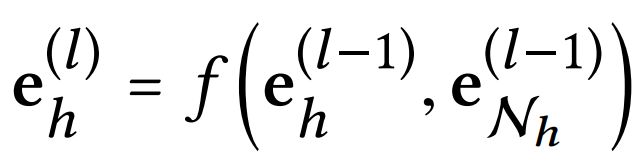
其中，$h$实体在$l-ego$第$l$阶的ego网络中传播的信息定义如下:

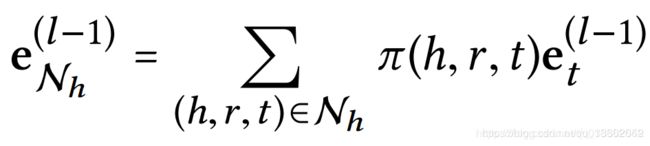
这个式子表示每个经过Softmax的注意力分数($\pi$)与其对应的值(实体e)相乘，这个过程会产生对应数量的对齐向量(alignment vector),我们通常称之为加权值。其中，$e_t^{l-1}$是从前面的信息传播步骤中由尾实体$t$产生的，包含着第$l-1$阶的所有邻点信息。所以高阶连通性如：

就可以通过以上四个过程得到了。（你看黄圈里面的$u_2$（在编码后叫做$e_{u_1}^{(3)}$不就和最左边的$u_1$连上了吗）。

注意这里还没有合并，只是通过递归得到了我想要的阶次的实体表示$e_h^{(l)}$而已。

4.3、Model Prediction

对应的是这一部分：

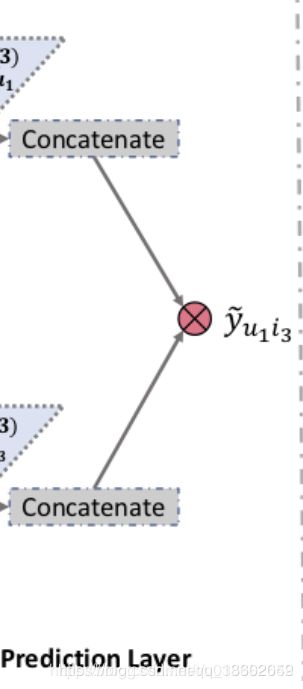
concatenate的输入是刚刚每层输出的各阶信息$e_h^{(l)}$(没错就是刚刚的加权值).通过分析不同layer的输出就可以得到从1到多阶的连通性,我们采用layer-aggregation机制（上文提到的另一种方法）进行concatenate这么多层的输出。(说白了就是对加权值求和，得到输出1）

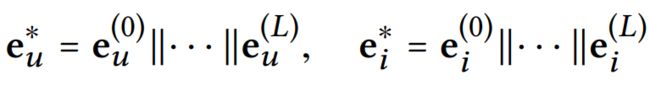
最后，我们对用户和项目的表示$e$进行内积，从而预测它们的匹配分数：

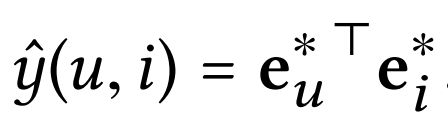
4.4、Optimization

作者综合了多种Loss模型，提出了分别对KG和CF两种Loss合并起来算Loss:

5、实验

在本部分，作者旨在回答以下三个问题：
1.KGAT模型是否能够超越目前的基线方法？
2.KGAT的不同模块对KGAT的影响程度如何？
3.KGAT的可解释性如何？

5.1、数据集描述

作者使用了三个数据集：Amazon-book，Last-FM，Yelp2018。具体信息如下表：

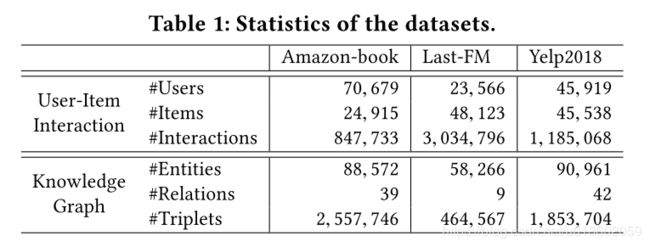
5.2、实验效果

作者通过与7个基线方法进行对比，结果如下：

不同数据集上用户的不同的数据分布的影响：

不同的层数对实验结果的影响：

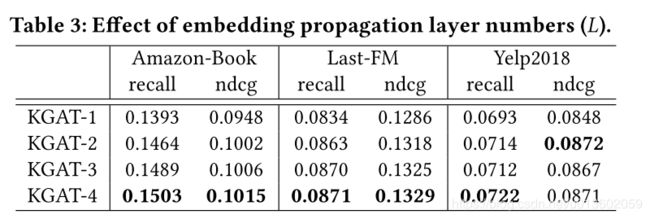
不同的聚合函数对实验结果的影响：

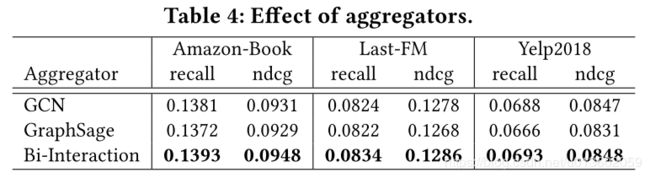
知识图嵌入与注意力机制的影响：
注意力可视化结果：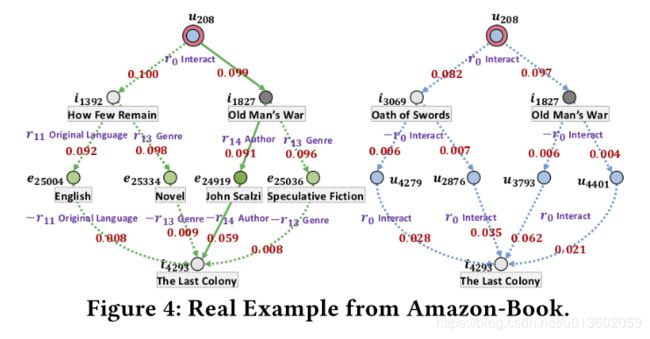

6、总结

整篇论文翻译链接